Composition-based Multi-Relational Graph Convolutional Networks 多关系图神经网络 ICLR 2020

论文来源:ICLR 2020
论文链接:https://arxiv.org/abs/1911.03082
代码链接:https://github.com/malllabiisc/CompGCN
1、引言
图神经网络已经成为图数据分析领域的经典算法了,各大顶会上相关的论文也层出不穷.但是,这些工作主要关注点都在如何在简单无向图上设计一个更新颖更复杂的模型,而没有从图数据的复杂程度来考虑.实际生活中的图往往更加复杂.比如,知识图谱上的有向多关系图.下面是一个知识图谱的例子,这里有多种节点,如London和United Kingdom;也有多种有向关系,如Born-in和Citizen-of.注意,这里的关系是有方向的,Born-in和Bord-in_inv是同一关系的两个方向.
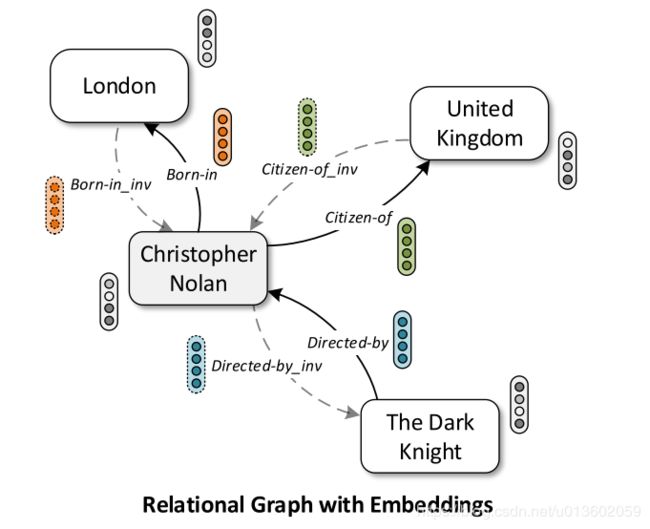
可以看出,多关系图的建模是更符合实际也具有更高的应用价值.本文作者从实际的图数据特点出发,设计了一种针对多关系有向图的图神经网络CompGCN来同时学习节点和关系的表示.同时,为了降低大量不同类型关系带来的参数,这里作者设计了一种分解操作composition operation,将所有关系都用一组基的加权组合来表示. 这样用于描述关系的参数只和基的个数有关.
下图对比了几种图神经网络的特点,可以看看出:学习关系的表示是CompGCN独有的特点.

总的来说,本文的贡献有3点:
- 设计了CompGCN模型,一种可以考虑多种关系信息的图神经网络框架,来同时学习节点和关系的表示.
- 证明了CompGCN与之前的多关系GNN之间的联系.
- 实验验证了CompGCN的有效性.
2、相关工作
首先,作者回顾了多关系图及多关系图神经网络的做法.
多关系图中的边可以表示为 ( u , v , r ) (u,v,r) (u,v,r),代表存在一条从节点 u u u指向节点 v v v的类型为 r r r的边,其中 r ∈ R r\in\mathcal{R} r∈R. 同时,也存在一个相应的反向边 ( u , v , r − 1 ) (u,v,r^{-1}) (u,v,r−1).
多关系图神经网络,也是分别聚合特定关系 r r r下的邻居,
H k + 1 = f ( A ^ H k W r k ) H^{k+1}=f(\hat{A}H^kW_r^k) Hk+1=f(A^HkWrk)其中, W r W_r Wr是针对关系 r r r的参数矩阵.而经典的单关系GCN聚合公式如下, H k + 1 = f ( A ^ H k W k ) H^{k+1}=f(\hat{A}H^kW^k) Hk+1=f(A^HkWk)可以看出,两者主要差异就在 W r W_r Wr和 W W W. 假设关系的种类非常多,那么参数矩阵 W r W_r Wr的个数也会非常多,引入了非常多的参数,不利于模型学习.
3、模型CompGCN
本文综合考虑多关系图上的3种边类型: 有向边 R \mathcal{R} R,如 ( u , v , r ) (u,v,r) (u,v,r); 反向边 R i n v \mathcal{R}_{inv} Rinv,如 ( u , v , r − 1 ) (u,v,r^{-1}) (u,v,r−1); 自连边 ⊤ \top ⊤, 如 ( u , v , ⊤ ) (u,v,\top) (u,v,⊤). 自连边指的是一个节点可以连接到自身,这种连接关系类型为 ⊤ \top ⊤. ε ′ = ε ∪ { ( u , v , r − 1 ∣ ( u , v , r ) ∈ ε } ∪ { ( u , v , ⊤ ) ∣ u ∈ V } \varepsilon'=\varepsilon\cup\{(u,v,r^{-1}|(u,v,r)\in\varepsilon\}\cup\{(u,v,\top)|u\in\mathcal{V}\} ε′=ε∪{(u,v,r−1∣(u,v,r)∈ε}∪{(u,v,⊤)∣u∈V}有了边的集合,相应的邻居集合也就可以得到了. 进一步,多关系图神经网络中聚合邻居的过程如下, h v = f ( ∑ ( u , r ) ∈ N ( v ) W r h u ) h_v=f(\sum_{(u,r)\in\mathcal{N}(v)}W_rh_u) hv=f((u,r)∈N(v)∑Wrhu)其中, ( u , r ) ∈ N ( v ) (u,r)\in\mathcal{N}(v) (u,r)∈N(v)是节点 v v v的在关系 r r r下的邻居集合, h v h_v hv是节点 v v v的表示, h u h_u hu是节点 u u u的表示, W r W_r Wr是针对关系 r r r的投影矩阵. 这里的 h u h_u hu综合考虑节点及边关系的影响,即: h u = ϕ ( x u , z r ) h_u=\phi(x_u,z_r) hu=ϕ(xu,zr)
本文设计了3种不同的[公式]函数
- Subtraction (Sub): ϕ ( x u , z r ) = x u − z r \phi(x_u,z_r)=x_u-z_r ϕ(xu,zr)=xu−zr
- Multiplication (Mult): ϕ ( x u , z r ) = x u ∗ z r \phi(x_u,z_r)=x_u*z_r ϕ(xu,zr)=xu∗zr
- Circular-correlation (Corr): ϕ ( x u , z r ) = x u ⋆ z r \phi(x_u,z_r)=x_u\star z_r ϕ(xu,zr)=xu⋆zr
考虑邻居节点的表示和边类型的区别,新的聚合公式如下: h v = f ( ∑ ( u , r ) ∈ N ( v ) W λ ( r ) ϕ ( x u , z r ) ) h_v=f(\sum_{(u,r)\in\mathcal{N}(v)}W_{\lambda(r)}\phi(x_u,z_r)) hv=f((u,r)∈N(v)∑Wλ(r)ϕ(xu,zr))其中, λ ( r ) \lambda(r) λ(r)是边的类型.回忆之前介绍的三种边类型:有向边,反向边,自连边.相应的投影矩阵也有3种.
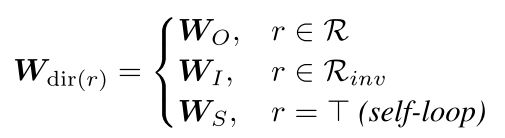
下图清晰的展示了有向边和反向边的聚合过程.
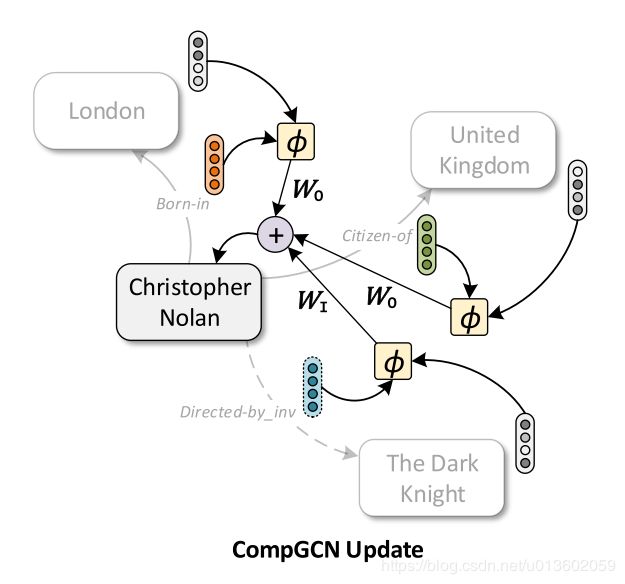
为了能够统一的对节点和边进行运算,我们需要把边的表示从边空间(如 z r z_r zr)投影到节点空间(如 h r h_r hr). h r = W r e l z r h_r=W_{rel}z_r hr=Wrelzr其中, W r e l W_{rel} Wrel是一个边空间到节点空间的投影矩阵.
CompGCN为了降低大量边带来的参数复杂度,这里作者设计了一组基向量 { v 1 , v 2 , ⋯ , v B } \{v_1,v_2,\cdots,v_{\mathcal{B}}\} {v1,v2,⋯,vB}.所有的边的表示都可以由一组基向量加权表示. z r = ∑ b = 1 B α b r v b z_r=\sum_{b=1}^{\mathcal{B}}\alpha_{br}v_b zr=b=1∑Bαbrvb其中, α b r \alpha_{br} αbr代表关系 r r r在基向量 v b v_b vb上的系数.
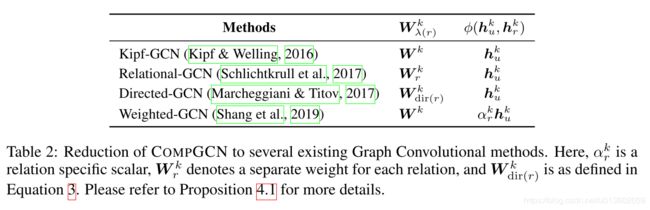
上述过程实际描述的是CompGCN第一层的聚合过程,涉及到节点/边的空间投影及边的组合表示. 在第二层及之后的聚合过程中并不需要投影/组合表示,聚合函数也有所不同. h v k + 1 = f ( ∑ ( u , r ) ∈ N ( v ) W λ ( r ) k ϕ ( h u k , h r k ) ) h_v^{k+1}=f(\sum_{(u,r)\in\mathcal{N}(v)}W_{\lambda(r)}^k\phi(h_u^k,h_r^k)) hvk+1=f((u,r)∈N(v)∑Wλ(r)kϕ(huk,hrk)) h r k + 1 = W r e l k h r k h_r^{k+1}=W_{rel}^kh_r^k hrk+1=Wrelkhrk最后作者分析了CompGCN与之前的一些模型的异同.可以看出,之前的很多图神经网络实际都可以认为是CompGCN的特例.
4、实验
这里,作者分别在链路预测,节点分类,图分类上进行了实验.
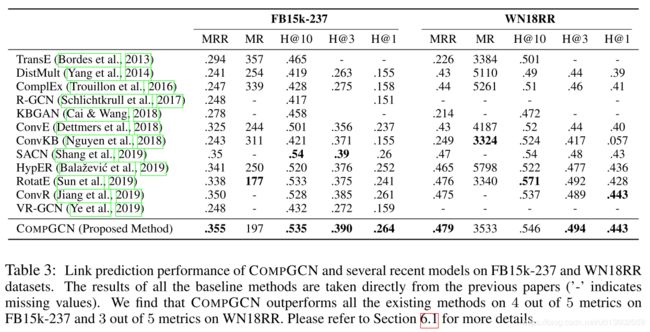
在链路预测任务上(见Table 3),CompGCN在大部分情况下取得了最优的效果.
作者进一步测试了不同composition operator的影响,见Table 4
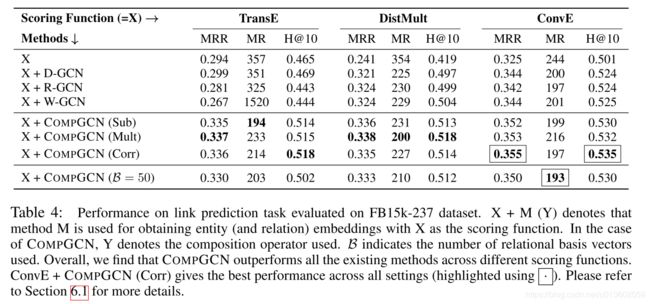
当采取CovE+CompGCN(Corr)的时候,模型取得了最佳的效果.
CompGCN的一个特点就是利用基向量来表示各个关系.作者进一步测试了基向量的个数对模型效果的影响.
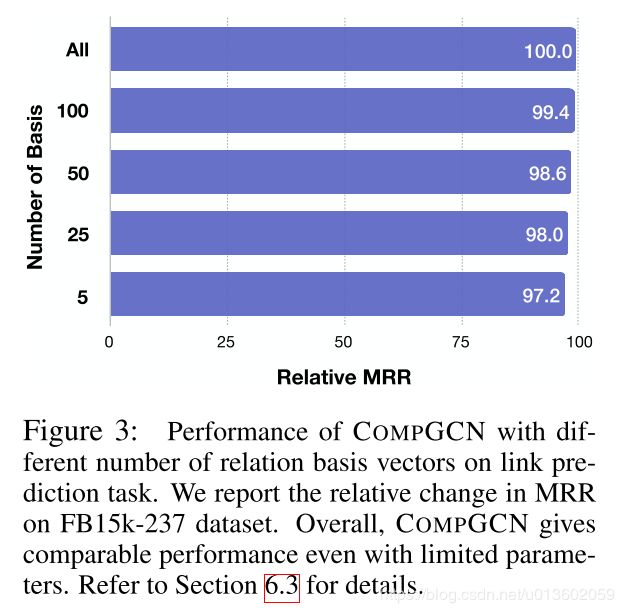
Figure 3可以看出,在基向量个数设置为100的时候,模型可以保持99.4%的效果.如果进一步降低基向量的个数,模型效果会持续下降.
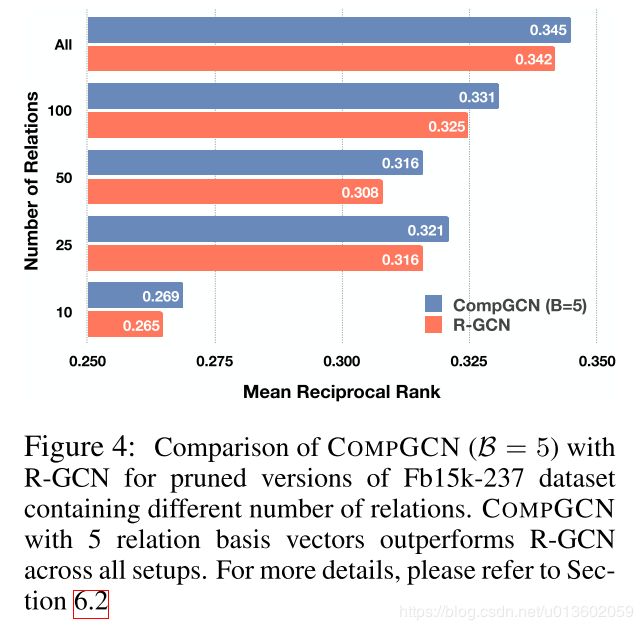
作者也测试了固定5个基向量的CompGCN与R-GCN的表现,见Figure 4.可以看出,即使只有5个基向量,CompGCN的效果也优于考虑所有关系的R-GCN.
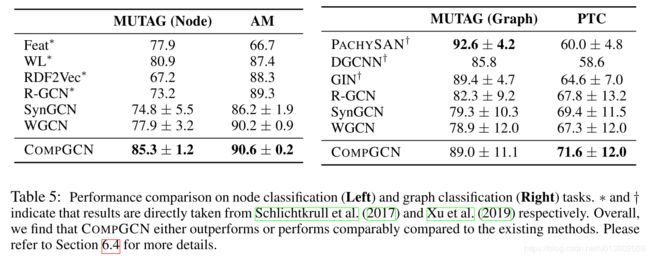
最后,作者也测试了CompGCN在节点分类/图分类上的效果,见Table 5. 在大部分情况下,CompGCN都取得了最好的效果.
5、结论
本文提出了一种针对多关系图的图神经网络CompGCN,可以同时学习到节点和边的表示. 通过一组基向量,CompGCN可以用较少的参数实现对大量关系的描述. 最后,作者通过大量的实验验证了CompGCN的有效性.