Group sample——比较有意思的人脸检测算法
论文:Group Sampling for Scale Invariant Face Detection
论文链接:http://openaccess.thecvf.com/content_CVPR_2019/papers/Ming_Group_Sampling_for_Scale_Invariant_Face_Detection_CVPR_2019_paper.pdf
这篇是发表在CVPR2019的关于人脸检测的文章,个人觉得是个很棒的工作,而且应该可以扩展到通用的目标检测算法。这篇文章的出发点是什么呢?我们知道不管是人脸检测还是通用目标检测,都会遇到输入图像中目标尺寸差异较大的情况,这种情况对检测效果最直观的影响就是小目标尺寸检测效果不好,因此CVPR2017提出的FPN算法基于融合后的多个特征层进行预测,很好地改善了这个问题。
但是FPN为什么有效呢?这篇文章通过各种对比实验发现:将FPN修改为基于单个特征层进行预测同样能够取得接近多个特征层的实验结果,而修改前后不同尺寸的样本数量分布非常类似,在此基础上作者继续探究不同尺寸的样本数量分布对检测效果效果的影响,最终得到一个结论:不同尺寸的样本数量不均衡是导致检测模型效果不好的原因,这个样本既包括正样本,也包括负样本,因此最后通过设计group sample操作使得不同尺寸的样本数量均衡,从而提升效果。
可以看出这篇论文其实是在揭示不同尺寸的样本分布情况对检测效果的影响,角度比较新颖。
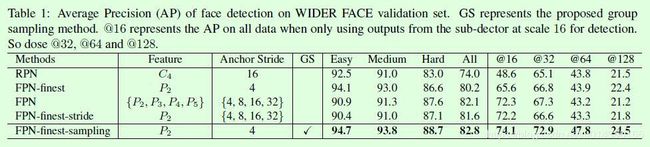
这篇文章基本上是围绕Figure1、Table1和Figure2来讲,读者可以对照着看。
在Figure1中作者列了5个网络,这5个网络是后续实验对比和论文创新点介绍的核心,注意看区别。(a)和(b)分别是RPN和FPN,这两个网络大家都比较熟悉,其中RPN是基于单个特征层进行预测的,这个特征层也就是(a)中画的C4,而FPN是基于多个特征层进行预测的,也就是(b)中的P2到P5,灰色框里面的数字,比如128/32,斜杠前面的数字表示anchor的尺寸,斜杠后面的数字表示铺设anchor时的stride,这两个数字大小都是针对输入图像的。那么(c)代表什么呢?(c)和(b)的差别主要在于预测的特征层从多个减少为1个。(d)和(c)的差别在于(d)中不同特征层铺设的anchor的stride都相同。(e)是这篇论文提出的算法:group sample,主要是在(d)的基础上增加了anchor的group sample操作。

Figure1的5个网络结构,总结起来主要有2个差别,1、anchor铺设的特征层数量不同,2、铺设anchor时设置的stride大小不同。这两种差别对效果影响有多大呢?在Table1中作者给出了非常详细的对比实验,依次来说几个重要的对比实验。
1、FPN和FPN-finest-stride,二者的差异在于用于预测的特征层数量不同,从Table1的实验结果可以看出二者之间的效果非常接近。FPN当时提出的时候主要是解决了原本基于单个特征层进行预测时在小尺寸目标上效果不好的问题,当时用于预测的单个特征层和输入图像之间的尺寸比例基本在1:16左右,显然小尺寸目标的特征就很有限。而FPN除了预测层从单个升级为多个外,还有一个重要的改进是深层和浅层特征的融合,二者不是一回事。这个实验作者主要是想证明FPN之所以有效,并不是用于预测的特征层数量增加导致的,而是深层和浅层特征的融合。其实这一点也体现在SSD上,SSD也基于多个特征层进行预测,但是没有做高层和浅层特征的融合,用过SSD的都知道SSD对小尺寸目标的检测效果不算很好。
2、FPN-finest-stride和FPN-finest,差别主要在于铺设anchor的stride不同,FPN-finest因为采用相同的stride,所以不同尺寸的负样本数量比较均衡,不同尺寸的正样本数量不均衡(类似RPN);而FPN-finest-stride中不同尺寸的正负样本数量差异都很大,这个实验重点就是观察这种差异带来的影响有多大。
3、FPN-finest-sampleing和FPN-finest-stride,这个实验主要是验证人为干预不同尺寸的样本分布对效果的影响有多大,人为干预的结果就是不同尺寸的正样本分布均衡,不同尺寸的负样本分布也均衡,效果上也可以看出提升是比较明显的。
看完前面的结构和实验结果,接下来就来看看作者是怎么深挖出这些实验结果背后的原因。
Figure2是关于5种网络结构的不同尺度anchor占比图,可以和Table1中的实验结果结合起来看。
(a)RPN中不同尺寸的负样本比例基本均衡,但是正样本占比随着尺寸的增大而增大,原因比较容易理解,RPN在铺设anchor时候,不同尺寸的anchor数量都是相同的(因为stride相同),但是因为大尺寸的anchor更容易成为正样本,因此尺寸越大的正样本占比越大。
(b)FPN因为基于多个特征层铺设anchor,可以看Figure1(b),P2层铺设尺寸为16,stride为4的anchor,P3层铺设尺寸为32,stride为8的anchor,显然在其他参数都相同的情况下,P2层的anchor数量是P3层anchor数量的4倍,因此可以看到Figure2(b)中的柱形图基本满足这样的4倍关系,其他层也是同理。
(c)FPN-finest-stride和FPN关于不同尺寸的正负样本分布是非常类似的,这就解释了为什么Table1中二者的实验结果类似的原因,也就是说在不同尺寸的正负样本分布类似的前提下,基于多个预测层进行预测和基于单个预测层进行预测没有太大差别。
(d)FPN-finest和FPN-finest-stride的差别主要在于铺设anchor的stride不同(可以参考Figure1),这就使得二者在不同尺寸的样本分布上存在较大差异。FPN-finest-stride的不同尺寸的正样本分布是不均衡的,不同尺寸的负样本分布差异更大,而且不管正样本还是负样本都是小尺寸的占比更大,因此FPN-finest-stride在小尺寸人脸(hard任务)上的效果要优于FPN-finest。FPN-finest的不同尺寸的负样本分布是均衡的,但是不同尺寸的正样本分布是不均衡的,而且正样本中大尺寸的占比要远大于小尺寸,因此FPN-finest在大尺寸人脸(Easy,Midium任务)上的效果要优于FPN-finest-stride。
(e)FPN-finest-sampling,基于前面的实验,作者猜测不同尺寸的样本数量(包括正样本和负样本)不均衡是导致检测效果不佳的原因,因此就尝试人为干预不同尺寸的样本分布,使得不同尺寸的正样本分布均衡,不同尺寸的负样本也分布均衡,如Figure2(e)所示,最后效果上确实比干预前(Figure2(d))要提升很多,参考Table1。

那么group sampling是怎么实现的呢?其实就是将正负样本按照尺寸大小分成不同的组(group),然后随机采样正样本使得每个组的正样本数量相同,同时因为每个组的样本数量是预先设定好的固定值(比如128、256),因此不同组的负样本数量也是相同的,这样就完成了人为干预的过程。
group sampling的思想很容易和OHEM、focal loss联系在一起,读者应该注意的是OHEM和focal loss主要是解决样本不均衡问题(图像样本层面),通过给予难例较大的损失权重来实现。group sampling虽然也是解决样本不均衡问题,但是一方面这里的不均衡是不同尺寸之间的样本不均衡,而不是不同标签之间的样本不均衡,另一方面这里的样本是anchor层面,不是图像样本层面,因此和OHEM、focal loss不完全一样。
实验结果:
Table2是针对FPN基于不同数量的特征层进行预测的实验对比,之前我们说过FPN真正有效的原因是深层和浅层特征的融合,从Table2的P3和C3的对比就可以看出来了。
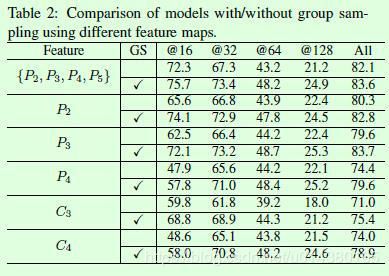
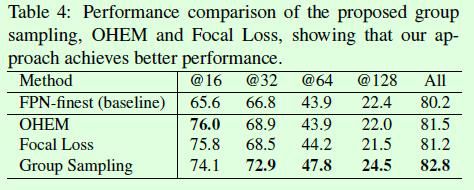
Table4是group sampling和OHEM、focal loss的效果对比,提升还是很明显的,其他更多实验结果可以参看论文。