THU数据结构编程作业一：祖玛（Zuma）

* 祖玛(Zuma) *

描述
祖玛是一款曾经风靡全球的游戏，其玩法是：在一条轨道上初始排列着若干个彩色珠子，其中任意三个相邻的珠子不会完全同色。此后，你可以发射珠子到轨道上并加入原有序列中。一旦有三个或更多同色的珠子变成相邻，它们就会立即消失。这类消除现象可能会连锁式发生，其间你将暂时不能发射珠子。

开发商最近准备为玩家写一个游戏过程的回放工具。他们已经在游戏内完成了过程记录的功能，而回放功能的实现则委托你来完成。

游戏过程的记录中，首先是轨道上初始的珠子序列，然后是玩家接下来所做的一系列操作。你的任务是，在各次操作之后及时计算出新的珠子序列。

输入
第一行是一个由大写字母’A’~’Z’组成的字符串，表示轨道上初始的珠子序列，不同的字母表示不同的颜色。

第二行是一个数字n，表示整个回放过程共有n次操作。

接下来的n行依次对应于各次操作。每次操作由一个数字k和一个大写字母Σ描述，以空格分隔。其中，Σ为新珠子的颜色。若插入前共有m颗珠子，则k ∈ [0, m]表示新珠子嵌入之后（尚未发生消除之前）在轨道上的位序。

输出
输出共n行，依次给出各次操作（及可能随即发生的消除现象）之后轨道上的珠子序列。

如果轨道上已没有珠子，则以“-”表示。

样例
Input

ACCBA
5
1 B
0 A
2 B
4 C
0 A

Output

ABCCBA
AABCCBA
AABBCCBA
-
A

限制
0 ≤ n ≤ 10^4

0 ≤ 初始珠子数量 ≤ 10^4

时间：2 sec

内存：256 MB

提示
列表

---

先上整个程序：

#include
#include
#include
#define MAXSIZE 20000
using namespace std;

const int SZ = 1<<20;  //fast io  
struct fastio{  
    char inbuf[SZ];  
    char outbuf[SZ];  
    fastio(){  
        setvbuf(stdin,inbuf,_IOFBF,SZ);  
        setvbuf(stdout,outbuf,_IOFBF,SZ);  
    }  
}io;  

int main(){
    #ifndef _OJ_
        freopen("input.txt", "r", stdin);
        freopen("output.txt", "w", stdout);
    #endif
    char s[MAXSIZE];    
    char c;
    int sz(0);//size of string
    scanf("%c", &c);
    while(c != '\n'){
        s[sz++] = c;
        scanf("%c",&c);     
    }
    s[sz++] = '\0';
    int Times;
    scanf("%d", &Times);

    int (*Insert)[2] = new int[Times][2]();
    for(int i = 0; i < Times; ++i)
        scanf("%d %c", &Insert[i][0], &Insert[i][1]);

    for(int i = 0, j = 0; i < Times; ++i){

        for( j = sz - 1; j >= Insert[i][0]; --j)
            s[j+1] = s[j];
        s[j+1] = Insert[i][1];
        ++sz;
        /*******************************/
        int Location = Insert[i][0];//insert site
        int p1= Location, p2 = Location, fix = Location;
        int P1 = Location, P2 = Location;
        int rep(1);//times of repetition
        bool p1Stop = false, p2Stop = false;
        while(!p1Stop || !p2Stop){
            //move p1
            while(!p1Stop){
                if(p1 > 0 && s[--p1] == s[fix])
                    ++rep;
                else
                    p1Stop = true;
            }
            //move p2
            while(!p2Stop){
                if(p2 < sz - 1 && s[++p2] == s[fix])
                    ++rep;
                else 
                    p2Stop = true; 
            }
            if(rep >= 3){
                if(s[p1] == s[fix])
                    P1 = p1;
                else
                    P1 = p1 + 1;
                if(s[p2] == s[fix] )
                    P2 = p2;
                else
                    P2 = p2 -1;
            }
            //reset rep
            if(rep >=3 && s[p1] == s[p2]){              
                rep = 2;
                fix = p1;
                p1Stop = false;
                p2Stop = false;
            }

        }

        if(P2 - P1 >= 2){
            for(int i = P1, j= P2;  j < sz - 1 ; ++i, ++j)
                s[i] = s[j + 1];
            sz -= (P2-P1+1);
        }


        /*******************************/   
/*
        bool Flag = true;
        if(sz >= 4){
            while(Flag){
                Flag = false;
                for(int i = 0; i < sz - 1; ++i){
                    int tt = 1;//counter to indicate the times of repetition
                    for(int j = i + 1; i < sz; ++j){
                        if(s[j] == s[i])
                            ++tt;
                        else
                            break;
                    }
                    if(tt >= 3){
                        Flag = true;
                        for(int k = i; k < sz-tt; ++k)
                            s[k] = s[k + tt];
                        sz -= tt;
                    }                   
                }
            }
        }
*/
        if(sz <= 1)
            printf("-\n");
        else
            printf("%s\n", s);

    }
    delete[] Insert;

    return 0;
}

以下对程序的部分内容进行解释：
1、 OJ上测试的数据量是非常大的，所以在设计程序时必须考虑时间复杂度。首先为了实现快速输入输出，调大流缓冲区。

const int SZ = 1<<20;   
struct fastio{   //fast io
    char inbuf[SZ];  
    char outbuf[SZ];  
    fastio(){  
        setvbuf(stdin,inbuf,_IOFBF,SZ);  
        setvbuf(stdout,outbuf,_IOFBF,SZ);  
    }  
}io; 

开始在OJ上测试时候总是只能通过95%，对于最后一组数据总是超时，而且在程序算法改进了以后（稍后会进行说明），依然超时，改进后的算法的时间复杂度应该是极大地降低了的。因为以前在自己的 linux 虚拟机上测试过数据量较大的数据总是出错，我就考虑到是否是和输入输出缓存有关系，毕竟自己只是刚入门的菜鸟，对缓存并没有足够的了解。在网上搜了很多，都提到了扩大缓冲区但是基本都没有解决方法。直到看到这位大神的代码，才恍然大悟：http://blog.csdn.net/baidu_23318869/article/details/41284075 。后来测试不仅最后一组数据通过而且速度也很快。我将这段代码加到前一个“范围查询”的程序中，速度果然加快了很多，膜拜大神~~~

2、虽然题目提示用列表解决，因为链表的插入和删除一个节点的时间复杂度为 O(1) ，但是我并没有使用列表，下次我想用列表重新实现一次。因为担心THU的OJ中没有c++的string头文件（上一篇的结尾已经解释），我用的是字符数组存储字符序列。注意为了方便输出我在数组的结尾插入了‘\0’，这样就可以以C字符串输出。关于需要插入的字符和插入的位置，我用了一个二维数组来存储，如下

int (*Insert)[2] = new int[Times][2]();
    for(int i = 0; i < Times; ++i)
        scanf("%d %c", &Insert[i][0], &Insert[i][1]);

虽然整个数组为整形，但是我通过 scanf 将数组的第二列调整输入为 char 型，这样就可以保存想要保存的数据，并能够方便获取。

3、程序的主题部分是个大的 for 循环。对于每一个有待插入的字符，首先进行插入 ：

 for( j = sz - 1; j >= Insert[i][0]; --j)
            s[j+1] = s[j];
        s[j+1] = Insert[i][1];
        ++sz;

后面就是对于连续出现的字符序列进行删除了。
起初，我使用的呗注释掉的那部分方法。通过对插入后的序列进行逐论扫描，每次扫描都删除一个连续字符序列，这种方法很笨但是确实很好实现。

bool Flag = true;
        if(sz >= 4){
            while(Flag){
                Flag = false;
                for(int i = 0; i < sz - 1; ++i){
                    int tt = 1;//counter to indicate the times of repetition
                    for(int j = i + 1; i < sz; ++j){
                        if(s[j] == s[i])
                            ++tt;
                        else
                            break;
                    }
                    if(tt >= 3){
                        Flag = true;
                        for(int k = i; k < sz-tt; ++k)
                            s[k] = s[k + tt];
                        sz -= tt;
                    }                   
                }
            }
        }

在OJ上测试后最后一组数据超时无法通过，我以为是因为自己的程序方法太笨复杂度较高引起的超时，其实主要的原因应该是前面提到的流缓存不够大的原因。但是以上错误的认为，让我不得不重新考虑算法的实现。

4、重新思考算法的实现。上面的方法在字符删除上耗时应该是最多了，每次都要对字符序列进行扫描，而且每次扫描只能删除一组重复序列，效率是很低的。于是，我希望找到一种方法提前知道哪些元素会被删除，最后一次性删除所有数据，这样就只需要一次删除操作。
想到了用指针的方法（我这里用的是数组的下标）进行标记。首先设置两个标志都指向插入点的字符，然后将两个标志分别向左和向右移动，记录字符，当左右指针对于同一个字符记录的次数大于等于3 的时候就说明两个指针之间的字符串是需要删除的。
整个过程如下图：

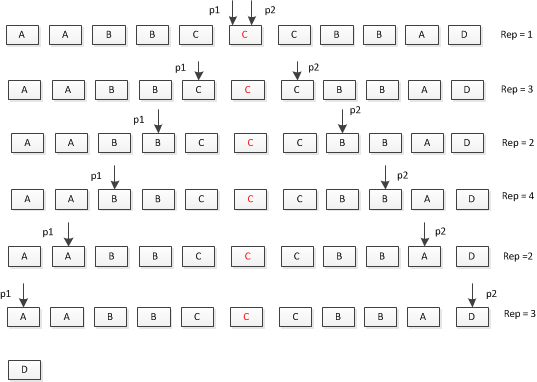
红色的 C 是插入的字符，Rep用来记录重复次数。
···首先指针p1和p2都指向插入位置，然后分别向左和向右移动直到遇到不同的字符就停止；
···如果当两个指针都停止时候的Rep的值大于等于3，则确定p1和p2之间的字符是需要删除的。
···此时，如果p1 和 p2 所指向的字符相同，则说明有可能后续的字符还需要删除，于是将Rep置为2，并再次移动p1和p2，同时记录Rep，如此反复。
···直到p1 和p2指向不同的字符或者已经移动到字符串两端。

整个过程也并不复杂，首先的难点是如果p1 和 p2 向两边移动停止时Rep小于3时，如何确定之前记录的需要删除的字符串的位置，我这里增加了两个变量P1 和P2来记录前一次确定需要删除的字符串的位置。其次，当其中一个指针移动到字符串的一端时，端点的字符串可能需要删除也可能不需要删除，这是比较难确定的。这里我增加了一个判断来解决这个问题：

if(rep >= 3){
        if(s[p1] == s[fix])
             P1 = p1;
        else
             P1 = p1 + 1;
        if(s[p2] == s[fix] )
              P2 = p2;
        else
              P2 = p2 -1;
            }

被这两个问题折磨的不要不要的~~~~ ヾ(≧O≦)〃嗷~
最后测试，发现运行明显快了不少。

另：写到这里，发现其实开始的插入操作也可以没有的，直接记录要插入的位置和字符，然后只需要做删除操作不就好了！发现自己智商又捉急了~ヾ(≧O≦)〃嗷~ヾ(≧O≦)〃嗷~ヾ(≧O≦)〃嗷~