深度学习笔记(二):各种梯度下降优化算法总结
1. 批量梯度下降 (Batch Gradient Descent)
定义代价函数为所有样本的代价
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum^m_{i=1}(h_{\theta}(x^{(i)})-y^{(i)})^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
θ j = θ j − α ⋅ ∇ θ j J ( θ ) ( f o r j = 0 : n ) \theta_j = \theta_j - \alpha\cdot\nabla_{\theta_j}J(\theta) (for j = 0 : n) θj=θj−α⋅∇θjJ(θ) (for j=0:n)
- 批量梯度下降,对所有样本计算梯度后求平均,并更新参数。
- 因为在执行每次更新时,我们需要在整个数据集上计算所有的梯度,所以批梯度下降法的速度会很慢,同时,批梯度下降法无法处理超出内存容量限制的数据集。批梯度下降法同样也不能在线更新模型,即在运行的过程中,不能增加新的样本。
- 对于凸误差函数,批梯度下降法能够保证收敛到全局最小值,对于非凸函数,则收敛到一个局部最小值
2. 随机梯度下降 (SGD)
在 SGD 中,定义代价函数为单一训练实例(随机选取)的代价
J ( θ ) = 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 ( f o r i = 1 : m ) J(\theta)=\frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2 (for i = 1 : m) J(θ)=21(hθ(x(i))−y(i))2 (for i=1:m)
更新参数
θ j = θ j − α ⋅ ∇ θ j J ( θ ; x ( i ) ; y ( i ) ) ( f o r j = 0 : n ) \theta_j=\theta_j-\alpha\cdot \nabla_{\theta_j}J(\theta;x^{(i)};y^{(i)}) (for j = 0 : n) θj=θj−α⋅∇θjJ(θ;x(i);y(i)) (for j=0:n)
- 与批量梯度下降相比,SGD 运行速度更快,SGD 在每次计算后便更新参数 θ \theta θ,而不需要首先将所有训练样本求和,可以用于在线学习
- SGD 的缺点在于:不是每一步都朝着正确的方向迈出,虽然会走向全局最小值,但可能无法站到最小值那一点上,而是在附近徘徊,因此使用 SGD 会一直持续波动;然而当我们缓慢减小学习率,SGD 与批量梯度下降具有同样的收敛行为。
3. 小批量梯度下降 (Mini-Batch Gradient Descent)
介于批量梯度下降和 SGD 之间的算法,即每次计算常数 b 个训练样本的误差,便更新一次参数。
定义代价函数为
J ( θ ) = 1 2 b ∑ k = i i + b − 1 ( h θ ( x ( k ) ) − y ( k ) ) 2 ( f o r i = 1 : m ) J(\theta)=\frac{1}{2b}\sum^{i+b-1}_{k=i}(h_{\theta}(x^{(k)})-y^{(k)})^2 (for i = 1 : m) J(θ)=2b1k=i∑i+b−1(hθ(x(k))−y(k))2 (for i=1:m)
更新参数
θ j = θ j − α ∇ θ j J ( θ ) ( f o r j = 0 : n ) \theta_j=\theta_j-\alpha\nabla_{\theta_j}J(\theta) (for j = 0 : n) θj=θj−α∇θjJ(θ) (for j=0:n)
4. 原始梯度下降的问题
- 在梯度平缓的区域下降缓慢,在梯度陡峭的区域容易抖动。
- 容易陷入局部极小值或鞍点。
- 选择一个合适的学习率比较困难。学习率太小会导致收敛的速度很慢,学习率太大会妨碍收敛,导致损失函数在最小值附近波动甚至偏离最小值。
5. 动量梯度下降法 (Momentum)
- Momentum 借用了物理中的动量概念,即,前几次的梯度也会参与运算。
- 为了表示动量,引入一个新的变量 v v v, v v v 是之前的梯度的累加,但每回合都有一定的衰减。
v v v 表示之前梯度的累加,这一点可以通过计算梯度的指数加权平均数实现,首先通过 Mini-batch 计算权重和偏置项的偏导数 d w , d b dw,db dw,db
令 v d w = β v d w + ( 1 − β ) d w , v d b = β v d b + ( 1 − β ) d b 令 v_{dw}=\beta v_{dw}+(1-\beta)dw,v_{db}=\beta v_{db}+(1-\beta)db 令 vdw=βvdw+(1−β)dw,vdb=βvdb+(1−β)db
β \beta β 一般设置为接近 1 的数,如 0.9, β \beta β代表了现在的 v d w v_{dw} vdw 和 v d b v_{db} vdb 与之前的 1 / ( 1 − β ) 1 / (1 - β) 1/(1−β) 个 d w dw dw 和 d b db db 有关
然后更新权重
w = w − α v d w , b = b − α v d b w=w-\alpha v_{dw},b=b-\alpha v_{db} w=w−αvdw,b=b−αvdb
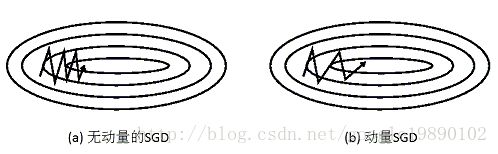
这样每一次梯度下降都会有一个之前的速度的作用,如果这次的方向与之前相同,则会因为之前的速度继续加速;如果这次的方向与之前相反,则会由于之前存在速度的作用不会产生一个急转弯,而是尽量把路线向一条直线拉过去。
这样就解决了梯度下降路线纵轴摆动较大的问题,同时也加快了横轴方向的学习速率。
6. Nesterov 动量梯度下降法
Nesterov 是对 Momentum 的一种改进:先对参数进行估计,然后使用估计后的参数来计算误差。
首先对参数进行临时更新: θ ~ = θ + α v \tilde{\theta}=\theta+\alpha v θ~=θ+αv
使用临时更新的参数计算误差用于求梯度: g = 1 m ∇ θ ~ ∑ i L ( f ( x i ; θ ~ ) , y i ) g = \frac{1}{m}\nabla_{\tilde{\theta}}\sum_i L(f(x_i;\tilde{\theta}),y_i) g=m1∇θ~∑iL(f(xi;θ~),yi)
计算速度更新: v = α v − ϵ g v=\alpha v-\epsilon g v=αv−ϵg
更新参数: θ = θ + v \theta=\theta+v θ=θ+v
其中,学习速率 ϵ \epsilon ϵ,初始参数 θ \theta θ,初始速率 v v v,动量衰减参数 α \alpha α
7. Adagrad 梯度下降法
Adagrad 的目的是为不同的参数设置不同的学习步长。
计算梯度:
g ~ = 1 m ∇ θ ∑ i L ( f ( x i ; θ ) , y i ) \tilde{g}=\frac{1}{m}\nabla_{\theta}\sum_iL(f(x_i;\theta),y_i) g~=m1∇θi∑L(f(xi;θ),yi)
累加梯度的平方: r = r + g ~ ⊙ g ~ r=r+\tilde{g}\odot\tilde{g} r=r+g~⊙g~
计算更新值: Δ θ = − η δ + r ⊙ g ~ \Delta\theta=-\frac{\eta}{\delta+\sqrt{r}}\odot\tilde{g} Δθ=−δ+rη⊙g~
由上式得,梯度越小,则学习步长越大,反之亦然;其中 δ \delta δ 是一个很小的数,为了防止分母为 0 ,常用 δ = 1 0 − 8 \delta=10^{-8} δ=10−8
更新参数: θ = θ + Δ θ \theta=\theta+\Delta\theta θ=θ+Δθ
存在问题:使用累加的方式计算梯度,但凡前面存在一个较大的梯度,往后就无法以较大的步长进行学习,但这也符合梯度下降中学习步长需要不断减小的规律;但问题是往后经过梯度平缓的区域就不能以较大的步长通过。
8. RMSprop 算法
RMSprop 是一种改进的 Adagrad,通过引入一个衰减系数,让累加得到的 r r r 每回合都衰减一定比例,这种方法很好地解决了 Adagrad 中步长过早变小的问题,适合处理非平稳目标,对于 RNN 效果很好。
首先计算梯度:
g ~ = 1 m ∇ θ ∑ i L ( f ( x i ; θ ) , y i ) \tilde{g}=\frac{1}{m}\nabla_{\theta}\sum_iL(f(x_i;\theta),y_i) g~=m1∇θi∑L(f(xi;θ),yi)
累加梯度的平方: r = ρ r + ( 1 − ρ ) g ~ ⊙ g ~ r=\rho r+(1-\rho)\tilde{g}\odot\tilde{g} r=ρr+(1−ρ)g~⊙g~
(这里未必是递增,计算的是当前和过往的滑动平均值)
计算更新值: Δ θ = − η δ + r ⊙ g ~ \Delta\theta=-\frac{\eta}{\delta+\sqrt{r}}\odot\tilde{g} Δθ=−δ+rη⊙g~
更新参数: θ = θ + Δ θ \theta=\theta+\Delta\theta θ=θ+Δθ
9. AdaDelta 算法
AdaDelta 与 RMSprop 一样也是为了解决 Adagrad 中步长过早变小的问题,但 AdaDelta 中没有学习率这一超参数。
同 RMSprop 一样计算累加梯度的平方: r t = ρ r t − 1 + ( 1 − ρ ) g ~ ⊙ g ~ r_{t}=\rho r_{t-1}+(1-\rho)\tilde{g}\odot\tilde{g} rt=ρrt−1+(1−ρ)g~⊙g~,
但 AdaDelta 会维护一个额外的状态变量 Δ x t \Delta x_t Δxt,其元素同样初始化为 0,接着使用 Δ x t − 1 \Delta x_{t-1} Δxt−1 计算自变量的变化量:
g t ′ = Δ x t − 1 + ϵ r t + ϵ ⊙ g t g'_t=\sqrt{\frac{\Delta x_{t-1}+\epsilon}{r_t + \epsilon}}\odot g_t gt′=rt+ϵΔxt−1+ϵ⊙gt
其中 ϵ \epsilon ϵ 是为了维持数值稳定性而添加的常数,如 10-e5。接着更新自变量
x t = x t − 1 − g t ′ x_t=x_{t-1}-g'_t xt=xt−1−gt′
最后使用 Δ x t \Delta x_t Δxt 来记录自变量来记录自变量 g t ′ g'_t gt′ 按元素平方的指数加权平均数
Δ x t = ρ Δ x t − 1 + ( 1 − ρ ) g ′ ⊙ g t ′ \Delta x_t=\rho \Delta x_{t-1}+(1-\rho) g'\odot g'_t Δxt=ρΔxt−1+(1−ρ)g′⊙gt′
如不考虑 ϵ 的影响,AdaDelta 算法与 RMSProp 算法的不同之处在于使用 Δ x t − 1 \sqrt{\Delta x_{t-1}} Δxt−1 来替代超参数 η \eta η 。
10. Adam 优化算法
Adam 基本上就是将 Momentum 和 RMSprop 结合在一起,即带动量的 RMSprop,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。
首先使用 Mini-batch 计算梯度:
g = 1 m ∇ θ ∑ i L ( f ( x i ; θ ) , y i ) g=\frac{1}{m}\nabla_{\theta}\sum_iL(f(x_i;\theta),y_i) g=m1∇θi∑L(f(xi;θ),yi)
计算一阶矩估计: s = ρ 1 s + ( 1 − ρ 1 ) g s=\rho_1 s+(1-\rho_1)g s=ρ1s+(1−ρ1)g
计算二阶矩估计: r = ρ 2 r + ( 1 − ρ 2 ) g ⊙ g r=\rho_2 r+(1-\rho_2)g\odot g r=ρ2r+(1−ρ2)g⊙g
修正偏差:由于 s , r s,r s,r 初始化为 0 向量,容易向 0 偏置,这样处理会减少这种偏置影响,其中 t t t 代表迭代次数
s ~ = s 1 − ρ 1 t \tilde{s}=\frac{s}{1-\rho^t_1} s~=1−ρ1ts
r ~ = r 1 − ρ 2 t \tilde{r}=\frac{r}{1-\rho^t_2} r~=1−ρ2tr
更新参数:
Δ θ = − α s ~ r ~ + δ \Delta\theta=-\alpha\frac{\tilde{s}}{\sqrt{\tilde{r}}+\delta} Δθ=−αr~+δs~
θ = θ + Δ θ \theta=\theta+\Delta\theta θ=θ+Δθ
其中,学习率 α \alpha α 需要经常调试, ρ 1 \rho_1 ρ1 常用 0.9, ρ 2 \rho_2 ρ2 常用 0.999, δ \delta δ 建议 1 0 − 8 10^{-8} 10−8