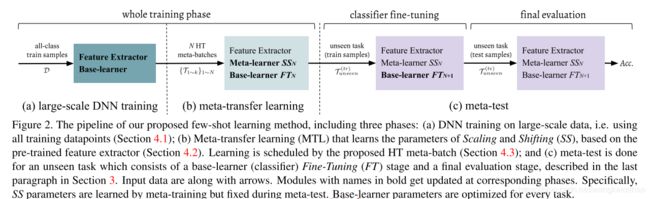
Meta-Transfer Learning for Few-Shot Learning 元迁移学习论文解读

我之前写过一篇元迁移学习的论文笔记，一种迁移学习和元学习的集成模型。
但是本文的元迁移学习方法完全不同于上一篇论文。

Abstract

由于深度神经网络容易对小样本过拟合，所以元学习倾向于使用浅层神经网络，但浅层神经网络限制了模型的性能。本文提出了meta-transfer learning(MTL)模型，MTL模型可以采用深层神经网络。其中，meta指的是训练多个任务，transfer指的是为深层神经网络的权重学习出缩放和移动函数(scaling and shifting functions)。同时本文还将hard task meta-batch模式作为课程学习中的课程引入了MTL。实验结果表明，MTL在多个任务上实现了最好的性能。

Contributions

1. 提出了meta-transfer lerning（MTL）方法，该方法综合应用了迁移学习和元学习的优点。
2. 将课程学习引入了元训练过程。

1 引言

通常而言，小样本学习方法可以被归为两类：数据增强方法和基于任务的元学习。数据增强一般指通过一种策略来增加样本数。

元学习方法比较典型的就是MAML了，MAML的任务无关的特性使得它可以应用于监督学习和无监督强化学习。但是，本文的作者认为MAML有一些局限性：

• 这些方法往往需要大量的相似任务作为元学习的输入，这种代价是很高的
• 每个任务都只能被复杂度较低的base learner训练，这样可以避免过拟合。

基于这些局限性，作者提出了MTL方法，并将课程学习引入了元训练中。

2 预备知识

2.1 元学习

元学习包括两个阶段：元训练和元测试。从任务分布$p(T)$中采样出一个任务$T$。$T$被划分为: 训练集$T^{(tr)}$用于优化base-learner，测试集$T^{(te)}$用于优化meta-learner。一个（模型）未见过的任务$T_{unseen}$将被用于meta-test阶段，最后的评估将在$T_{unseen}^{(te)}$。

meta-training阶段，这个阶段致力于在多个任务上学习出一个meta-learner。这个阶段包含两个步骤，第一个步骤是对base-learner的参数进行更新，第二个步骤是对meta-learner的参数进行更新。

meta-test阶段，这个阶段将会测试训练出的Meta-learner在新任务上的拓展性能。给定$T_{unseen}$，meta-learner ${\tilde{\theta }}_T$通过某种方法教base-learner ${\theta }_T$快速地适应新任务$T_{unseen}$。

3 方法

如上图所示，MTL模型包括三个阶段：

1. 使用大规模数据训练一个深层神经网络，同时将低层固定为特征提取器
2. MTL为特征提取神经元学习出缩放和移动参数，为了提高总的学习效果，作者使用了Hard-task meta-batch策略。
3. 执行典型的meta-test阶段。

3.1 在大规模数据上训练深层神经网络

作者将所有类别的数据合并起来一起用于预训练，比如作者将64个类别每个类别所有600个样本均作为输入进行训练，从而训练出一个分64类的分类器。

作者首先将特征抽取器$\Theta$（比如ResNets中的卷积层）和分类器$\theta$（比如ResNets最后的全连接层）随机初始化，然后使用梯度下降法对它们进行优化：
$$[\Theta ;\theta ]=:[\Theta ;\theta ]-\alpha \nabla L_D([\Theta ;\theta ]),$$
其中,L指的是下面的经验损失，
$$L_D([\Theta ;\theta ])=\frac{1}{|D|}\sum _{(x,y)\in D}l(f_{\Theta ;\theta }(x),y),$$
这个阶段将学习出特征抽取器$\Theta$。它将在下面的元训练和元测试阶段被固定住，而学习出的分类器$\theta$将被丢弃，因为接下来的任务中将包含不同的分类目标，比如5-class分类而不是训练时的64-class分类。

3.2 元迁移学习(MTL)

MTL模型通过Hard-Task meta-batch训练来优化”缩放和移动“操作（缩放和移动操作，即Scaling and Shifting (SS)可以简洁的表示为$\alpha X+\beta$）。下图展示了通过SS和Fine-Tunning操作进行更新的区别。SS操作，表示为${\Phi }_{S_1}$和${\Phi }_{S_2}$，在学习时并没有改变固定住的$\Theta$的值，但是Fine-Tuning操作更新的是整个$\Theta$。

下面将详细介绍SS操作。给定一个任务T,则当前base-learner的参数${\theta }^{\prime }$的更新方法为：
$${\theta }^{\prime }\leftarrow \theta -\beta {\nabla }_{\theta }{L}_{T^{(tr)}}([\Theta ;\theta ],{\Phi }_{S_{\{1,2\}}}),$$
在这个式子中，$\Theta$没有被更新。需要注意的是，这里的$\theta$与前面的大规模分类器中的$\theta$并不相同。

$\Phi$通过测试损失值$T^{te}$来优化，
$${\Phi }_{S_i}=:{\Phi }_{S_i}-\gamma {\nabla }_{{\Phi }_{S_i}}{L}_{T^{(te)}}([\Theta ;{\theta }^{\prime }],{\Phi }_{S_{\{1,2\}}}).$$
在这步中，$\theta$的学习率与式（4）中相同：
$$\theta =:\theta -\gamma {\nabla }_{\theta }{L}_{T^{(te)}}([\Theta ;{\theta }^{\prime }],{\Phi }_{S_{\{1,2\}}}).$$
与式（3）相比，式（5）中的${\theta }^{\prime }$来自于在$T^{(tr)}$的最后一轮base-learning。

接下来，我们描述一下作者如何将${\Phi }_{S_{\{1,2\}}}$应用于固定的神经元。

给定训练后的$\Theta$，它的第$l$层包含$K$个神经元，我们有$K$对参数，分别为权重和偏置，记作$(W_{i,k},b_{i,k})$。

假定$X$为输入，我们在$(W,b)$上应用$\{{\Phi }_{S_{\{1,2\}}}\}$:
$$SS(X;W,b;{\Phi }_{S_{\{1,2\}}})=(W⨀{\Phi }_{S_1})X+(b+{\Phi }_{S_2})$$

4.3 Hard task meta-batch

传统情况下的meta-batch由随机采样的任务组成。作者将模型预测错误的样本收集在一起重新组成一个更难的任务，然后重新训练。这就是hard task meta-batch。

SS操作的参数通过$T^{(te)}$的损失进行优化。我们可以得到模型在$T^{(te)}$上分别对$M$个类别的准确率，然后根据准确率大小进行排序。作者将学习设置成动态的在线学习，所以我们将从准确率较低的类别中重新对任务进行采样和训练。

4.4 算法

算法1总结了大规模深层神经网络的训练（第1-5行）和元-迁移学习（第6-22行）。第16-20行展示的是Hard Task meta-batch的重采样和连续训练阶段。

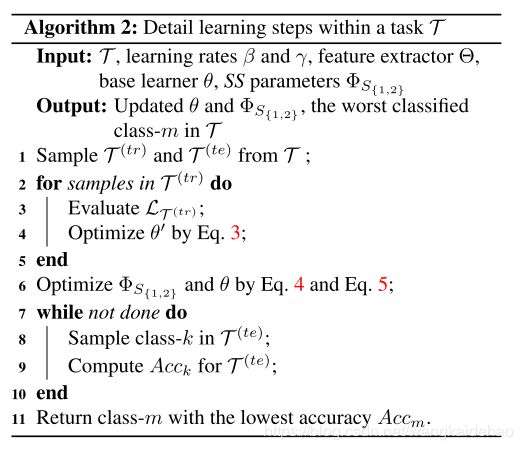
算法2展示的是在单个任务上的学习过程。

5 实验

5.1 数据集和实现细节

作者在两个benchmarks上进行了实验，miniImageNet 和 Fewshot-CIFAR100数据集。

• miniImageNet有100个类别，每个类别有600个样本，这100个类别被划分为：64,16,20类，分别用于meta-trianing, meta-validation和meta-test阶段。

• Fewshot-CFAR100包括100个类别，每个类别有600个样本，每个样本的尺寸是$32\times 32$。这100个类别属于20个超类。超类的划分为$12:4:4$，分别用于训练，验证和测试。

**特征抽取器$\Theta$**使用的是ResNet-12，它包括4个残差块，每个残差块包含3个$3\times 3$的卷积层，以及1个$2\times 2$的最大池化层。

5.2 实验结果

5.2.1 miniImageNet

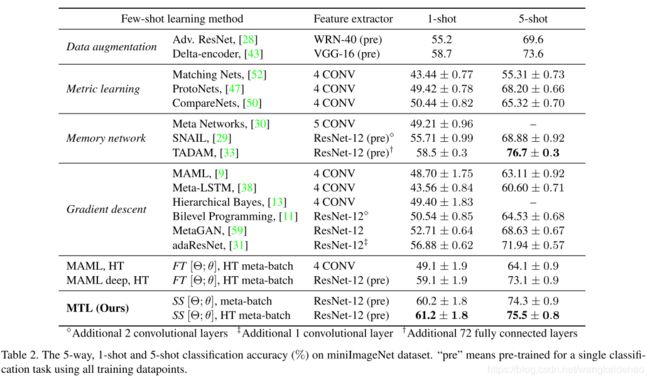
上表展示了各个方法在miniImageNet数据集上的实验结果。可以看到MTL+SS+Hard task meta-batch方法取得了最好的实验结果。

5.2.2 FC100

6 结论

本文提出了MTL模型，并使用Hard task meta-batch的课程学习策略进行训练。MTL模型独立于任何特定的网络，它可以被很好的进行拓展。而且Hard task meta-batch策略可以很容易地在在线迭代中使用。