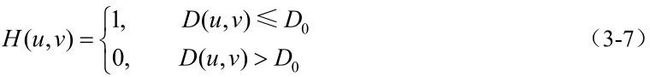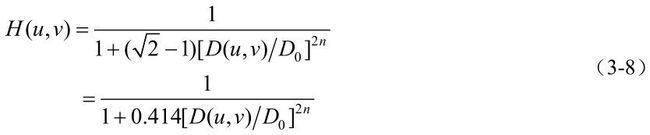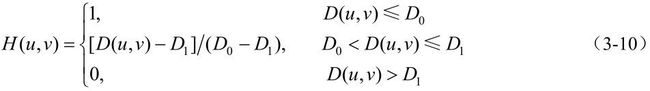一、何为图像噪声?噪声是妨碍人的感觉器官所接受信源信息理解的因素,是不可预测只能用概率统计方法认识的随机误差。
举个例子:
从这个图中,我们可以观察到噪声的特点:1>位置随机 2>大小不规则。我们将这种噪声称为随机噪声(random noise),这是一种非常常见的噪声类型。
二、噪声的类型
噪声可以借用随机过程以及概率密度函数(Probability Density Function,PDF)来描述,通常可采用其数组特征,即均值,方差,相关函数等。按照概率密度函数分为高斯噪声、瑞利噪声、伽马噪声、指数分布噪声、均匀分布噪声、脉冲噪声、泊松噪声等。有的噪声与图像信号的强度不相关,如图像传输过程引入的信道噪声、摄像机扫描噪声等,这种噪声称为加性噪声(additive noise)。常见的加性噪声按照概率密度函数特征分为短拖尾加性噪声(如均匀分布噪声)、中拖尾加性噪声(高斯分布噪声)、长拖尾加性噪声(如指数分布噪声)、脉冲噪声(如椒盐噪声、随机数脉冲噪声等)。
有的噪声与图像信号有关,往往随着图像信号的变化而变化,如光照变化引起的噪声、飞机扫描图像中的噪声、电视扫描光栅中的相干噪声、斑点噪声等。这种噪声称为乘性噪声(multiplicative noise)。
matlab向图中添加噪声的指令:
I1=imnoise(I,type,parameters);
其中,当type为gaussian,所加入噪声是parameters为m(均值)、v(方差)的高斯噪声,这是最普通的噪声。
当type为localvar时,所加入噪声是parameters为0(均衡)、v(方差)的高斯噪声。
当type为poission时,所加入的是无参数的泊松噪声,在照度非常小时出现,或在高倍电子放大线路中出现。
当type为salt&pepper时,所加入的噪声是parameters为d(密度)的椒盐噪声。
当type为speckle时,所加入的噪声是parameters为0(均值)、v(方差)的均匀分布噪声(斑点噪声)。
例子1:向图像中加入椒盐噪声matlab示例。
I=imread('eight.tif');
J=imnoise(I,'salt & pepper',0.02);
subplot(121),imshow(I),title('原始图像');
subplot(122),imshow(J),title('加入椒盐噪声的图像');
例子2:利用多帧图像平均法,对受零均值随机高斯噪声干扰的图像进行平滑处理
I=imread('eight.tif');
[m,n]=size(I);
I1=zeros(m,n);
for i=1:16
I2(:,:,i)=imnoise(I,'gaussian',0,0.01);%由原始图像叠加随机高斯噪声生成1-16帧图像
I1=I1+double(I2(:,:,i));%多帧带有随机噪声的图像叠加
if or(or(i==1,i==4),or(i==8,i==16));
figure,imshow(uint8(I1/i))%取平均并显示结果
end
end
分别显示施加噪声后的图像和叠加平均后的图像,可以发现叠加平均图像的数量级越多,噪声消除效果越好,对16帧图像取平均后几乎消除了所有噪声。
三、图像平滑消除噪声
对于只有一帧带有噪声的图像是无法用上述方法消除噪声的,此时又该怎么办呢?根据噪声的特点可以知道噪声的灰度与其周围的灰度之间有明显的灰度差,因此造成了视觉障碍。此时消除噪声的方法要利用图像平滑(image smoothing),简称平滑(smoothing),因此如何把边缘部分与噪声部分区分开,只消除噪声是图像平滑的关键所在。
图像平滑的方法可分为频率域法(频率法)和空间域法(空域法)两类。频域法的处理基础是傅里叶变换和低通滤波技术,空域法的处理基础是模板卷积。
(1)低通滤波(lowpass filter)
低通滤波属于频域平滑滤波法,通过滤除高频成分,保留低频成分,在频域中实现平滑处理。其滤波公式为G(U,V)=H(U,V)F(U,V),其中F(U,V)是原始图像频谱,G(U,V)是平滑图像频谱,H(U,V)是传递(转移)函数。
步骤:将原始图像f(x,y)进行傅里叶变换,把图像从空间域变换到频率域,得到图像频谱F(U,V),再通过传递函数H(U,V)用低通滤波公式改变F(U,V),最后对滤波处理后的频谱G(U,V)进行傅里叶反变换,即可得到过滤后的图像g(x,y)。
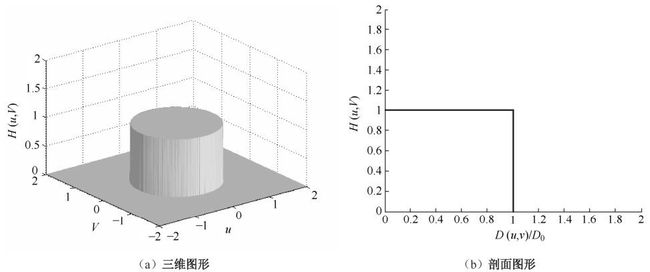
1.理想低通滤波器(Ideal Low-Pass Filter,ILPF)的传递函数
D0是截止频率,D(u,v)=(u^2+v^2)^(1/2)为频率平面原点到点(u,v)的距离。其特点是物理上不可实现,有抖动现象,滤除高频成分使图像变模糊。
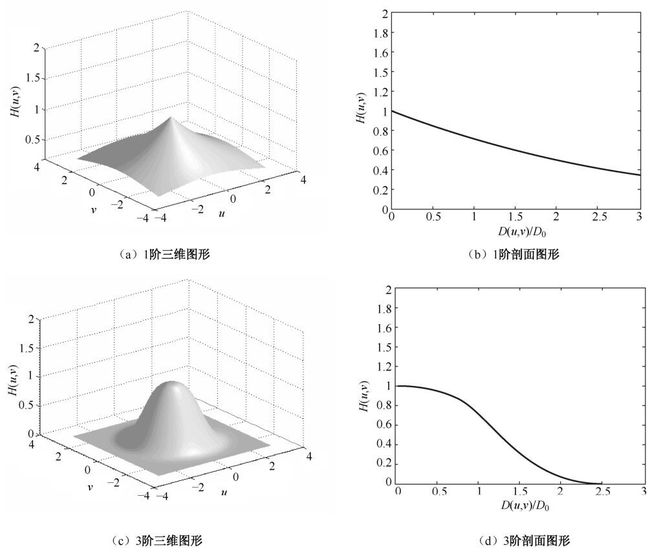
2.巴特沃斯低通滤波器(Butterworth Low-Pass Filter,BLPF)具有如下传递函数
与理想低通滤波器不同,该滤波器的传递函数不是在D0处突然不连续,而是平滑过渡。当H(U,V)降为最大值的1/2时,D(U,V)=D0。n为阶数,阶数越大,传递函数越陡峭。
3.指数形低通滤波器(Exponential Low-Pass Filter,ELPF)具有如下传递函数:
当D(U,V)=D0时,H(u,v)降为最大值的1/(2^(1/2))时的频率可作为截止频率。
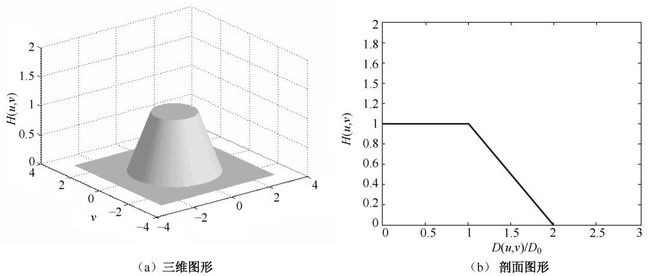
4.梯形低通滤波器(Trapezoidal Low-Pass Filter,TLPF)具有如下传递函数:
例子:巴特沃斯低通滤波器
%巴特沃斯低通滤波器
I=imread('eight.tif');
I1=imnoise(I,'salt & pepper');
figure,imshow(I1);
f=double(I1);
g=fft2(f);%傅里叶变换
g=fftshift(g);%直流分量移到频谱中心
[M,N]=size(g);%计算图像的高和宽
d0=50;nn=2;%截止频率为50的二阶巴特沃斯低通滤波器
m=round(M/2);n=round(N/2);%数据取整
for i=1:M
for j=1:N
d=sqrt((i-m)^2+(j-n)^2);%计算频率平面原点到各点的距离
h=1/(1+0.414*(d/d0)^(2*nn));%传递公式
result(i,j)=h*g(i,j);%滤波公式
end
end
result=ifftshift(result);%直流分量移回到左上角
I2=ifft2(result);%傅里叶反变换
I3=uint8(real(I2));%取幅值并转换成8位无符号整数
figure,imshow(I3);