回想起第一次看到正则表达式的时候,眼睛里大概都是 $7^(0^=]W-\^*d+,心里我是拒绝的。不过在后面的日常工作里,越来越多地开始使用到正则表达式,正则表达式也逐渐成为一个很常用的工具。
要掌握一种工具除了了解它的用法,了解它的原理也是同样重要的,一般来说,正则引擎可以粗略地分为两类:DFA(Deterministic Finite Automata)确定性有穷自动机和 NFA (Nondeterministic Finite Automata)不确定性有穷自动机。
使用 NFA 的工具包括.NET、PHP、Ruby、Perl、Python、GNU Emacs、ed、sec、vi、grep的多数版本,甚至还有某些版本的egrep和awk。而采用 DFA 的工具主要有egrep、awk、lex和flex。也有些系统采用了混合引擎,它们会根据任务的不同选择合适的引擎(甚至对同一表达式中的不同部分采用不同的引擎,以求得功能与速度之间的最佳平衡)。 —— Jeffrey E.F. Friedl《精通正则表达式》
DFA 与 NFA 都称为有穷自动机,两者有很多相似的地方,自动机本质上是与状态转换图类似的图。(注:本文不会严格给自动机下定义,深入理解自动机可以阅读《自动机理论、语言和计算导论》。)
NFA
一个 NFA 分为以下几个部分:
- 一个初始状态
- 一个或多个终结状态
- 状态转移函数
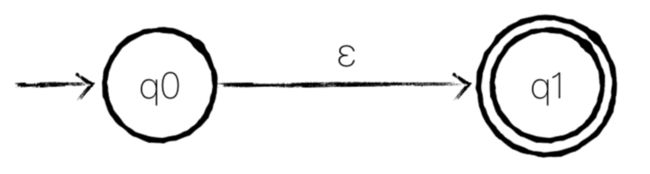
上图是一个具有两个状态 q0 和 q1 的 NFA,初始状态为 q0(没有前序状态),终结状态为 q1(两层圆圈标识)。在 q0 上有一根箭头指向 q1,这代表当 NFA 处在 q0 状态时,接受输入 a,会转移到状态 q1。
当要接受一个串时,我们会将 NFA 初始化为初始状态,然后根据输入来进行状态转移,如果输入结束后 NFA 处在结束状态,那就意味着接受成功,如果输入的符号没有对应的状态转移,或输入结束后 NFA 没有处在结束状态,则意味着接受失败。
由上可知这个 NFA 能接受且仅能接受字符串 a。
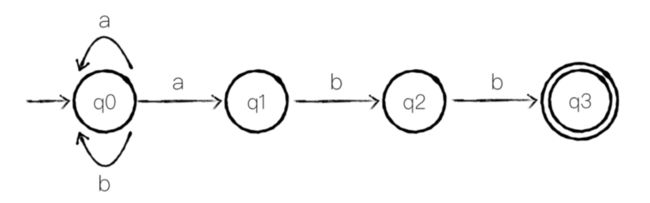
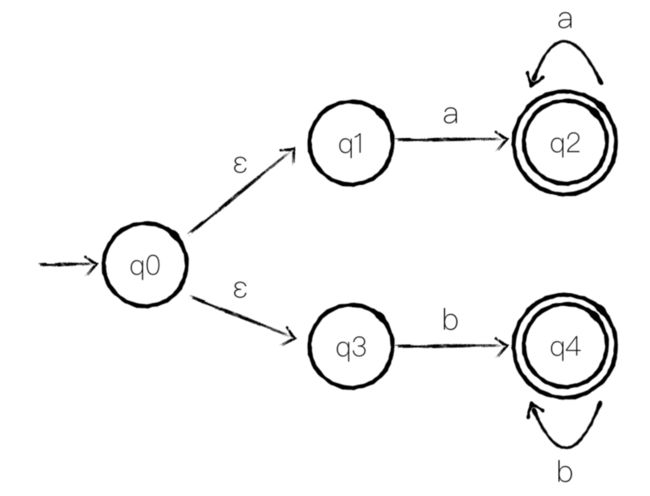
那为什么叫做 NFA 呢,因为 对于同一个状态与同一个输入符号,NFA 可以到达不同的状态,如下图:
在 q0 上时,当输入为 a,该 NFA 可以继续回到 q0 或者到达 q1,所以该 NFA 可以接受 abb(q0 -> q1 -> q2 -> q3),也可以接受 aabb(q0 -> q0 -> q1 -> q2 -> q3),同样接受 ababb、aaabbbabababb 等等,你可能已经发现了,这个 NFA 表示的正则表达式正是 (a|b)*abb
ε-NFA
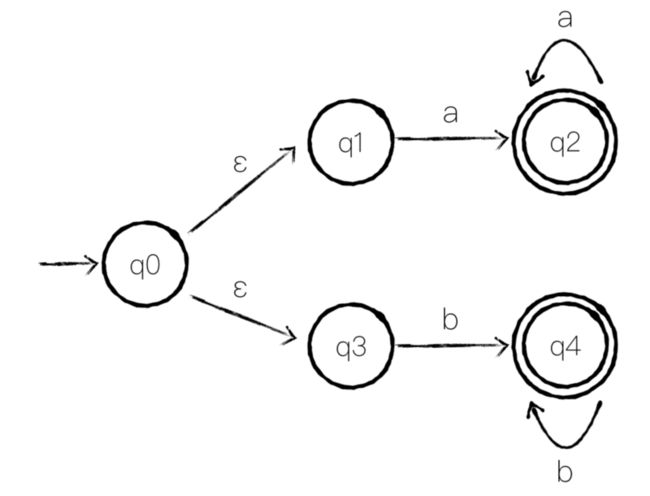
除了能到达多个状态之外,NFA 还能接受空符号 ε,如下图:
这是一个接受 (a+|b+) 的 NFA,因为存在路径 q0 -ε-> q1 -a-> q2 -a-> q2,ε 代表空串,在连接时移除,所以这个路径即代表接受 aa。
你可能会觉得为什么不直接使用 q0 通过 a 连接 q2,通过 b 连接到 q4,这是因为 ε 主要起连接的作用,介绍到后面会感受到这点。
DFA
介绍完了不确定性有穷自动机,确定性有穷自动机就容易理解了,DFA 和 NFA 的不同之处就在于:
- 没有
ε转移 - 对于同一状态和同一输入,只会有一个转移
那么 DFA 要比 NFA 简单地多,为什么不直接使用 DFA 实现呢?这是因为对于正则语言的描述,构造 NFA 往往要比构造 DFA 容易得多,比如上文提到的 (a|b)*abb,NFA 很容易构造和理解:
但直接构造与之对应的 DFA 就没那么容易了,你可以先尝试构造一下,结果大概就是这样:
所以 NFA 容易构造,但是因为其不确定性很难用程序实现状态转移逻辑;NFA 不容易构造,但是因为其确定性很容易用程序来实现状态转移逻辑,怎么办呢?
神奇的是每一个 NFA 都有对应的 DFA,所以我们一般会先根据正则表达式构建 NFA,然后可以转化成对应的 DFA,最后进行识别。
McMaughton-Yamada-Thompson 算法
McMaughton-Yamada-Thompson 算法可以将任何正则表达式转变为接受相同语言的 NFA。它分为两个规则:
基本规则
归纳规则
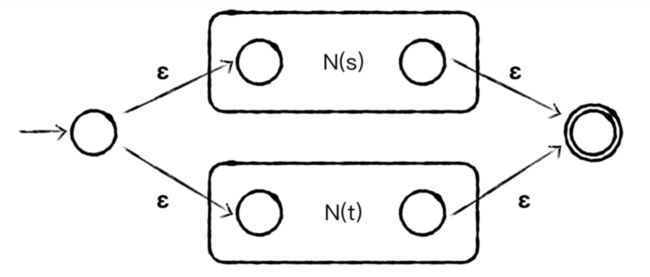
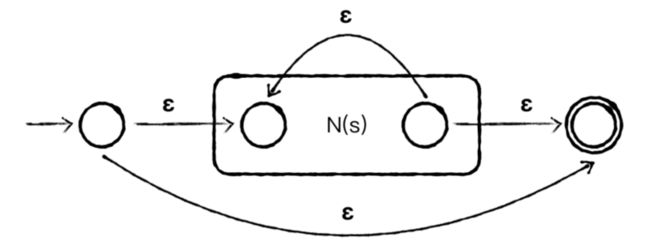
假设正则表达式 s 和 t 的 NFA 分别为 N(s) 和 N(t),那么对于一个新的正则表达式 r,则如下构造 N(r):
并
当 r = s|t,N(r) 为
连接
当 r = st,N(r) 为
闭包
当 r = s*,N(r) 为
其他的 +,? 等限定符可以类似实现。本文所需关于自动机的知识到此就结束了,接下来就可以开始构建 NFA 了。
基于 NFA 实现
1968 年 Ken Thompson 发表了一篇论文 Regular Expression Search Algorithm,在这篇文章里,他描述了一种正则表达式编译器,并催生出了后来的 qed、ed、grep 和 egrep。论文相对来说比较难懂,implementing-a-regular-expression-engine 这篇文章同样也是借鉴 Thompson 的论文进行实现,本文一定程度也参考了该文章的实现思路。
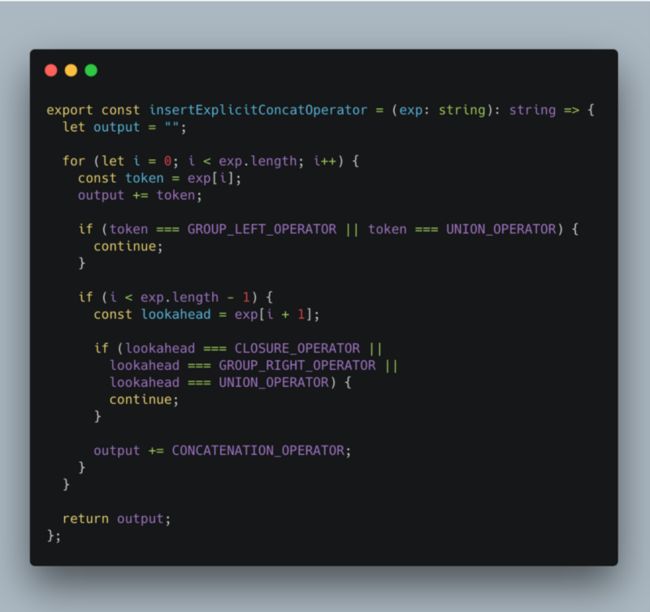
添加连接符
在构建 NFA 之前,我们需要对正则表达式进行处理,以 (a|b)*abb 为例,在正则表达式里是没有连接符号的,那我们就没法知道要连接哪两个 NFA 了。
所以首先我们需要显式地给表达式添加连接符,比如 ·,可以列出添加规则:
| 左边符号 / 右边符号 | * | ( | ) | 并 | 字母 |
|---|---|---|---|---|---|
| * | ❌ | ✅ | ❌ | ❌ | ✅ |
| ( | ❌ | ❌ | ❌ | ❌ | ❌ |
| ) | ❌ | ✅ | ❌ | ❌ | ✅ |
| 并 | ❌ | ❌ | ❌ | ❌ | ❌ |
| 字母 | ❌ | ✅ | ❌ | ❌ | ✅ |
(a|b)*abb 添加完则为 (a|b)*·a·b·b,实现如下:
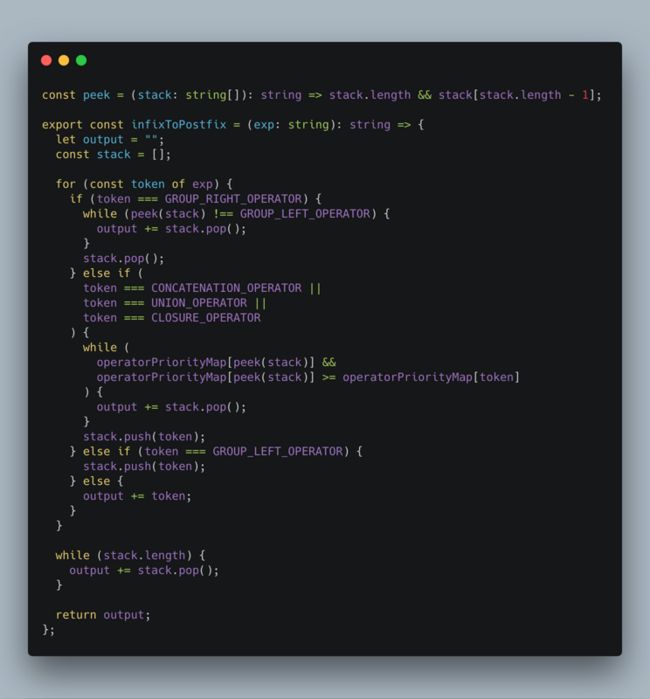
中缀表达式转后缀表达式
如果你写过计算器应该知道,中缀表达式不利于分析运算符的优先级,在这里也是一样,我们需要将表达式从中缀表达式转为后缀表达式。
在本文的具体过程如下:
- 如果遇到字母,将其输出。
- 如果遇到左括号,将其入栈。
- 如果遇到右括号,将栈元素弹出并输出直到遇到左括号为止。左括号只弹出不输出。
- 如果遇到限定符,依次弹出栈顶优先级大于或等于该限定符的限定符,然后将其入栈。
- 如果读到了输入的末尾,则将栈中所有元素依次弹出。
在本文实现范围中,优先级从小到大分别为
- 连接符
· - 闭包
* - 并
|
实现如下:
如 (a|b)*·c 转为后缀表达式 ab|*c·
构建 NFA
由后缀表达式构建 NFA 就容易多了,从左到右读入表达式内容:
- 如果为字母 s,构建基本 NFA
N(s),并将其入栈 - 如果为
|,弹出栈内两个元素N(s)、N(t),构建N(r)将其入栈(r = s|t) - 如果为
·,弹出栈内两个元素N(s)、N(t),构建N(r)将其入栈(r = st) - 如果为
*,弹出栈内一个元素N(s),构建N(r)将其入栈(r = s*)
代码见 automata.ts
构建 DFA
有了 NFA 之后,可以将其转为 DFA。NFA 转 DFA 的方法可以使用 子集构造法,NFA 构建出的 DFA 的每一个状态,都是包含原始 NFA 多个状态的一个集合,比如原始 NFA 为
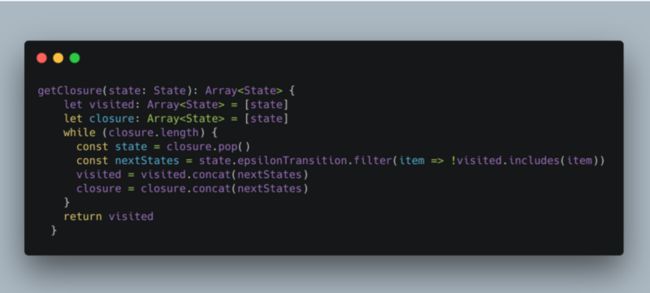
这里我们需要使用到一个操作 ε-closure(s),这个操作代表能够从 NFA 的状态 s 开始只通过 ε 转换到达的 NFA 的状态集合,比如 ε-closure(q0) = {q0, q1, q3},我们把这个集合作为 DFA 的开始状态 A。
那么 A 状态有哪些转换呢?A 集合里有 q1 可以接受 a,有 q3 可以接受 b,所以 A 也能接受 a 和 b。当 A 接受 a 时,得到 q2, 那么 ε-closure(q2) 则作为 A 状态接受 a 后到达的状态 B。同理,A 状态接受 b 后到达的 ε-closure(q4) 为状态 C。
而状态 B 还可以接受 a,到达的同样是 ε-closure(q2),那我们说状态 B 接受 a 还是到达了状态 B。同样,状态 C 接受 b 也会回到状态 C。这样,构造出的 DFA 为
DFA 的开始状态即包含 NFA 开始状态的状态,终止状态亦是如此。
搜索
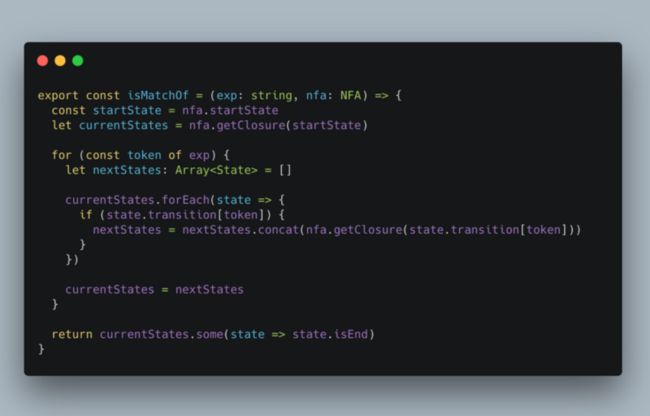
其实我们并不用显式构建 DFA,而是用这种思想去遍历 NFA,这本质上是一个图的搜索,实现代码如下:
getClosure 代码如下:
总结
总的来说,基于 NFA 实现简单的正则表达式引擎,我们一共经过了这么几步:
- 添加连接符
- 转换为后缀表达式
- 构建 NFA
- 判断 NFA 是否接受输入串
完整代码见 github