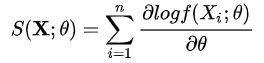2019独角兽企业重金招聘Python工程师标准>>> ![]()
深度模型的训练的基本依据是最小化模型拟合数据的误差。旨在不仅知其然(如何构建和训练一个深度模型),还应知其所以然(为什么这样训练,可以做哪些优化)。我们就会发现,有很多研究者,在面向一些特定问题下,深度模型训练算法中的误差函数定义也就有很多种。而万变不离其宗,如果想设计有效的新颖Loss函数,可以参考的“宗”便是统计学理论,概率论。例如,Loss 如果是square loss,就是最小二乘,SVM 的loss是Hinge Loss,Boosting的是exp-loss,Logistics Regression则是log-loss。
比如 《Faster Gaze Prediction With Dense Networks and Fisher Pruning》提出了采用Fisher information 来指导精准化地深度模型的pruning(剪枝)。感兴趣的读者可以阅读这篇论文。推荐精读这篇文章,是因为它是一篇 以“数学理论” 指导 “深度模型优化”的文章。深度模型发展至此,它在不同应用(图片,视频,活动,文本等)中的可用性和影响力无需多说,但是关于深度模型的可解释性一直是个open problem。深度模型的优化也应走 “朴素理论指导深度模型实践的路线”来尝试探索深度模型的可解释性。
在我的观点里,深度模型像是一个高度抽象的统一框架,满足了人们对整洁美的追求,它拥有一种神秘的超自然力量。只要按照固定模式构建和训练深度神经网络,它总能work。 但其弊端也很明显,如果研究者不在概率方法下一些功夫,不太能真正理解其原理,更不能做深度模型的优化。我们尽管承认了深度模型有不能解释的因素,但是我们依然需要想尽办法让这种【不可解释性】的程度最小。
这篇短文将探索几个统计学概念。目的是探索什么是Fisher information,Hessain 矩阵,似然估计。它们在 “统计学”这一被充分验证充分接受的理论体系下有什么联系? 如何被应用在深度模型的优化中?
一, 似然估计
在统计学中,似然估计又称作概率估计,是用来估计概率模型参数的一个方法。最大似然估计 会寻找关于参数的最可能的值。从数学上来讲,可以在参数的所有可能取值中寻找一个使得似然函数取到最大值。这个使可能性最大的参数值即称作参数的最大似然估计。
最大似然估计是,利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
最大化一个似然函数 和 最大化它的自然对数是等价的。因为自然对数log是一个连续且在似然函数的值域内严格递增的凸函数,而求对数可以一定程度上简化运算。求样本所有观测的联合概率最大化,是个联乘积,只要取对数,就变成了线性加总。 此时,通过对参数求导数,并令一阶导数为零,就可以通过解方程(组),得到最大似然估计值。
似然函数是一种可能性函数,它的自然对数跟信息熵以及Fisher信息紧密相连。
二. 信息熵
信息熵,应该理解为不确定性的度量,而不是确定性的度量,因为信源(信息,指来自分布或数据流中的事件、样本或特征)的随机性越大,其熵越大。
信息熵定义为概率分布的对数的相反数。 也就是,事件的概率分布和每个事件的信息量构成了一个随机变量,这个随机变量的均值(即期望)就是这个分布产生的信息量的平均值(即熵)。
信息熵越高,可传达的信息越多(同理于,1个 八进制 比 二进制 字符传递的信息多)。 例如,英文文本的熵比较低,因为英语容易被预测,qu的组合总是比q与其它任何字母的组合多。英文文本的熵大概只有4.7比特。
(1948年,克劳德.艾尔伍德.香农,将物理中热力学的熵,引入到信息论,因此它又称作香农熵)
三. Hessian矩阵
Jacobian矩阵类似于一阶导数,Hessian矩阵相当于二阶导数。一阶导数的零点是函数的极值点,二阶导数的零点就是一阶导数的极值点。一阶导数的零点不用多说,二阶导数的零点也很重要。比如,在信号处理中,信号的一阶导数的极值点反映信号变化的最剧烈程度。极值点寻求在编程时不方便,不如找二阶导数的零点。
四. Fisher 信息
Fisher 信息被应用在机器学习的目标优化,深度学习的梯度下降优化(泛化),深度模型剪枝中。
Fisher信息阵,得名于英国著名统计学家 Ronald Fisher。Fisher矩阵是一个统计学中极其重要且核心的概念,从统计学的观点方面探讨很多。本节主要Focus在帮助理解Fisher信息在深度学习中应用的一些相关的内容。
Fisher信息量(阵)是统计学的一个重要结果。在经典统计中,它被用来表示无偏估计类方差的下界与最大似然估计的渐进方差。在贝叶斯统计中它被用来表示无信息先验分布。
似然估计的一阶导数,叫做score function,如下所示:
那么Fisher信息,就是这个score function的二阶矩阵 E[S(X; \theta)]。它也定义了score的方差。
因此,Fisher Information的第一条数学意义:就是用来估计方差。它的直观表述就是,随着收集的数据越来越多,这个方差由于是一个Independent sum的形式,也就变的越来越大,也就象征着得到的信息越来越多。
如果log likelihood二阶可导,在一般情况下(under specific regularity conditions)满足:
于是得到了Fisher Information的第二条数学意义:log likelihood在参数真实值处的负二阶导数的期望。在真实参数上,log likelihood的梯度的协方差矩阵和log likelihood的Hessian相等。
对于一个log likelihood function,它越平而宽,就代表我们对于参数估计的能力越差,它高而窄,就代表我们对于参数估计的能力越好,也就是信息量越大。而这个log likelihood在参数真实值处的负二阶导数,就反应了这个log likelihood在顶点处的弯曲程度,弯曲程度越大,整个log likelihood的形状就越偏向于高而窄,也就代表掌握的信息越多。一个直观解释就是,Fisher Information反映了我们对参数估计的准确度,它越大,对参数估计的准确度越高,即代表了越多的信息。
以下文字参考Zhangxing Zhu知乎: https://zhuanlan.zhihu.com/p/34394897
Fisher信息在机器学习(ml)目标函数优化中的理解
Ml 中要解决的优化问题多数是最小化某个 negative log likelihood,往往通过梯度下降或者 SGD 进行迭代求解一般较慢,因为没有考虑到参数的不同维度的尺度不一样对目标函数影响不一样,经典优化的牛顿法就解决这个问题来加速优化算法的收敛,
但是,在某些问题中(代码)求解evaluate 二阶导是不可行的,根据 Fisher 和 Hessian 的相等关系【对某些机器学习模型尤其是深度模型,计算全Hessian矩阵比Fisher信息所需要的计算量大,求解困难】。因此,一个取代的方法,就是将 Fisher替换为 H,这个方法叫 Fisher scoring,
在 ml 中大家称这种方法为 natural gradient,amari那本《information geometry》 里介绍很详细:沿着 Remannian manifold做优化。当然 natural gradient 也可以从trust-region 方法下优化 KL距离得出,最终的结果殊途同归。
Natural gradient 的科研很多,比如如何高效的计算高维矩阵的逆,根据问题做某些近似(用在 CNN 中的优化里,K-FAC方法),去年 nips又将 k-fac 用到强化学习中,效果也不错。 还有一个早几年的工作是,将 natural gradient 用到 stochastic variational inference中,David Blei的工作。
直观地,大家会想到这个 gradient的 covariance matrix 可以乘在梯度前面做 preconditioning来加速优化,很少想到它还有其他的作用。有研究者(https://zhuanlan.zhihu.com/p/34394897)发现这个神奇 gradient covariance的结构特点是 SGD 在深度学习中有良好泛化能力的重要原因之一。
具体地,
容易想到:这个 covariance 和目标函数的 curvature 存在某种联系,在真实参数上是相等的。但在SGD 迭代过程中是否相等呢?答案是,二者是近似相等的。 具体可以参考文章《The regularization Effects of Anisotropic Noise in Stochastic Gradient Descent: Its Behavior of Escaping from Minima and Regularization Effects》
那么,在近似相等的情况下,可以发现:SGD 的 noise diffusion 是遵循目标函数的曲率信息的,也就是在大的特征值方向,幅度要大,带来的直接效果是SGD 会很容易的逃离那些 sharp minima 跑到比较稳定的 flat minima, 而最近的研究表明 flat minima 往往泛化能力更好。也就是 SGD 的天然梯度噪声的结构帮助算法找到泛化好的解,这样的噪声结构要优于Langevin dynamics, 即直接在完整梯度上加各向同性的噪声。.