哈希表的原理和使用(C++代码)
文章目录
- 一、概念
- 二、散列表的构造方法
- 2.1 直接定址法
- 2.2 除留取余法
- 2.3 数字分析法
- 2.4 折叠法
- 2.5 平方取中法
- 三、冲突解决方法
- 3.1 开放地址法
- 3.1.1 线性探测法
- 3.1.2 平方探测法
- 3.2 链地址法
一、概念
散列技术是在记录的存储位置和他的关键字之间建立一个确定的对应关系f,是的每个关键字key对应一个存储位置f(key)。查找时,根据这个对应的关系找到给定值key的映射f(key),若查找集合中存在这个记录,则必定在f(key)的位置上。我们把这种对应关系f成为散列函数,又称为哈希(Hash)函数。采用散列技术将记录存储在一块连续的存储空间中,这块连续空间称为散列表或哈希表(Hash-Table)。
二、散列表的构造方法
2.1 直接定址法
直接定址法使用下面的公式
f ( k e y ) = a × k e y + b , b 为 常 数 f(key) = a×key+b,b为常数 f(key)=a×key+b,b为常数
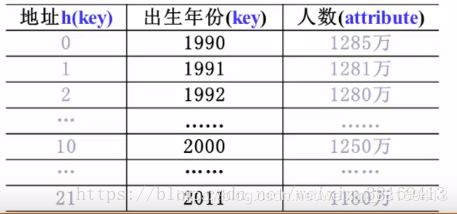
比如统计出生年份,那么就可以使用 f ( k e y ) = k e y − 1990 f(key) = key-1990 f(key)=key−1990来计算散列地址。
2.2 除留取余法
这种方法是最常用的散列函数构造方法,对于表长为m的散列公式为
f ( k e y ) = k e y m o d p ( p ≤ m ) f(key)=key \mod p (p \leq m) f(key)=keymodp(p≤m)
2.3 数字分析法
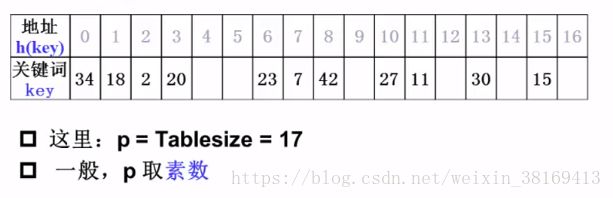
分析数字关键字在各位上的变化情况,取比较随机的位作为散列地址这里使用一个手机号码作为例子,手机号码是一个字符串,一般的说,后面4位是真正的用户号。

2.4 折叠法
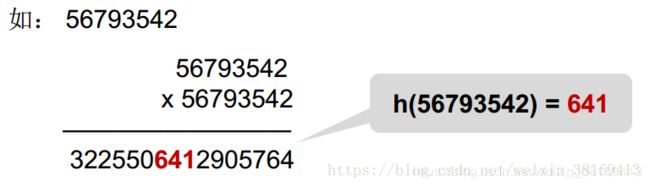
2.5 平方取中法
三、冲突解决方法
常用处理冲突的思路:
- 换个位置:
开放地址法 - 同一位置的冲突对象组织在一起:
链地址法
3.1 开放地址法
一旦产生了冲突(该地址已有其它元素),就按某种规则去寻找另一空地址.若发生了第 i 次冲突,试探的下一个地址将增加 d i d_i di, 基本公式是:
h i ( k e y ) = ( h ( k e y ) + d i ) m o d T a b l e S i z e ( 1 ≤ i < T a b l e S i z e ) h_i(key) = (h(key)+d_i) \mod TableSize ( 1≤ i < TableSize ) hi(key)=(h(key)+di)modTableSize(1≤i<TableSize)
这里面 d i d_i di 决定了不同的解决冲突方案: **线性探测、平方探测、双散列。**下面依次介绍各中方法。
3.1.1 线性探测法
线性探测法以增量序列 1 , 2 , … … , ( T a b l e S i z e − 1 ) 1, 2, ……,(TableSize -1) 1,2,……,(TableSize−1)循环试探下一个存储地址。
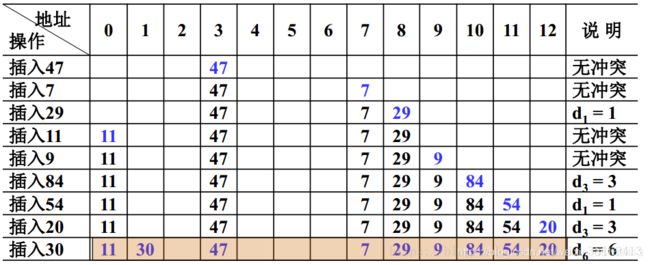
【例1】 设关键词序列为 47 , 7 , 29 , 11 , 9 , 84 , 54 , 20 , 30 {47, 7, 29, 11, 9, 84, 54, 20, 30} 47,7,29,11,9,84,54,20,30,散列表表长 T a b l e S i z e = 11 TableSize =11 TableSize=11 (装填因子 α = 9 / 13 ≈ 0.69 α= 9/13 ≈ 0.69 α=9/13≈0.69),散列函数为: h ( k e y ) = k e y m o d 11 h(key) = key \mod 11 h(key)=keymod11。 用线性探测法处理冲突,列出依次插入后的散列表,并估算查找性能。
【解】 初步的散列地址如下表所示。
| 关键词 ( k e y ) (key) (key) | 47 | 7 | 29 | 11 | 9 | 84 | 54 | 20 | 30 |
|---|---|---|---|---|---|---|---|---|---|
| 散列地址 h ( k e y ) h(key) h(key) | 3 | 7 | 7 | 0 | 9 | 7 | 10 | 9 | 8 |
可以看出,有多个关键词的散列地址发生了冲突,具体见下表。
| 关键词 ( k e y ) (key) (key) | 47 | 7 | 29 | 11 | 9 | 84 | 54 | 20 | 30 |
|---|---|---|---|---|---|---|---|---|---|
| 散列地址 h ( k e y ) h(key) h(key) | 3 | 7 | 7 | 0 | 9 | 7 | 10 | 9 | 8 |
| 冲突次数 | 0 | 0 | 1 | 0 | 0 | 3 | 1 | 3 | 6 |
这里引出一下散列表的的查找性能分析,散列表的查找性能,一般有两种方法
成功平均查找长度(ASLs)不成功平均查找长度 (ASLu)
对于上面一题的散列地址冲突次数为
| 散列地址 h ( k e y ) h(key) h(key) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 关键词 ( k e y ) (key) (key) | 11 | 30 | 47 | 7 | 29 | 9 | 84 | 54 | 20 | ||||
| 冲突次数 | 0 | 6 | 0 | 0 | 1 | 0 | 3 | 1 | 3 |
ASLs: 查找表中关键词的平均查找比较次数(其冲突次数加1)
A S L s = ( 1 + 7 + 1 + 1 + 2 + 1 + 4 + 2 + 4 ) / 9 = 23 / 9 ≈ 2.56 ASLs = (1+7+1+1+2+1+4+2+4) / 9 = 23/9 ≈ 2.56 ASLs=(1+7+1+1+2+1+4+2+4)/9=23/9≈2.56
ASLu:不在散列表中的关键词的平均查找次数(不成功)
一般方法:将不在散列表中的关键词分若干类。
如:根据H(key)值分类
A S L u = ( 3 + 2 + 1 + 2 + 1 + 1 + 1 + 9 + 8 + 7 + 6 ) / 11 = 41 / 11 ≈ 3.73 ASL u= (3+2+1+2+1+1+1+9+8+7+6) / 11 = 41/11 ≈ 3.73 ASLu=(3+2+1+2+1+1+1+9+8+7+6)/11=41/11≈3.73
- 参考代码
#include3.1.2 平方探测法
平方探测法以增量序列 1 2 , − 1 2 , 2 2 , − 2 2 , . . . , q 2 1^2 ,-1^2 ,2^2 ,-2^2 ,...,q^2 12,−12,22,−22,...,q2,且 q ≤ ⌊ T a b l e S i z e / 2 ⌋ q ≤ \lfloor TableSize/2 \rfloor q≤⌊TableSize/2⌋ 循环试探下一个存储地址。还是使用[例1],得到的冲突如下表
| 关键词 key | 47 | 7 | 29 | 11 | 9 | 84 | 54 | 20 | 30 |
|---|---|---|---|---|---|---|---|---|---|
| 散列地址h(key) | 3 | 7 | 7 | 0 | 9 | 7 | 10 | 9 | 8 |
| 冲突次数 | 0 | 0 | 1 | 0 | 0 | 2 | 0 | 3 | 3 |
A S L s = ( 1 + 1 + 2 + 1 + 1 + 3 + 1 + 4 + 4 ) / 9 = 18 / 9 = 2 ASLs =(1+1+2+1+1+3+1+4+4)/ 9 = 18/9 = 2 ASLs=(1+1+2+1+1+3+1+4+4)/9=18/9=2

- 参考代码
/*******************************************************************************
功 能:哈希表——平方探测法(+/- 1^2,2^2,3^2...)
创建时间: 2018-07-24
作 者:Elvan
修改时间:
作 者:
********************************************************************************/
#include 3.2 链地址法
链地址法就是将相应位置上冲突的所有关键词存储在同一个单链表中
【例2】 设关键字序列为 47 , 7 , 29 , 11 , 16 , 92 , 22 , 8 , 3 , 50 , 37 , 89 , 94 , 21 47, 7, 29, 11, 16, 92, 22, 8, 3, 50, 37, 89, 94, 21 47,7,29,11,16,92,22,8,3,50,37,89,94,21,散列函数取为 h ( k e y ) = k e y m o d 11 h(key) = key \mod 11 h(key)=keymod11,用分离链接法处理冲突。
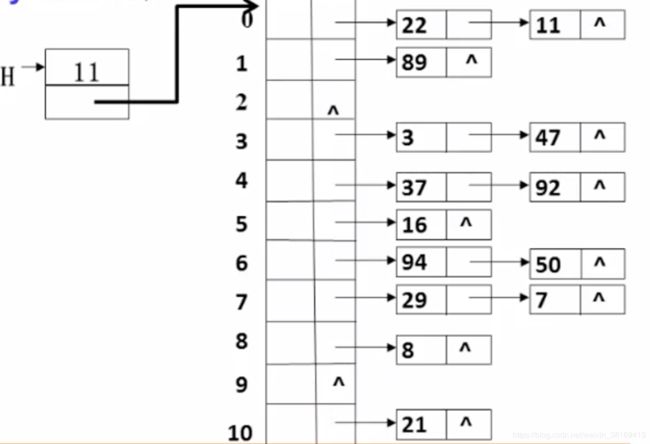
【解】表中有9个结点只需1次查找,5个结点需要2次查找,所以查找成功的平均查找次数为
A S L s = ( 9 + 5 ∗ 2 ) / 14 ≈ 1.36 ASLs=(9+5*2)/ 14 ≈ 1.36 ASLs=(9+5∗2)/14≈1.36
- 参考代码
/*******************************************************************************
功 能:哈希表——链表法(+/- 1^2,2^2,3^2...)
创建时间: 2018-07-24
作 者:Elvan
修改时间:
作 者:
********************************************************************************/
#include