java实现数据结构之二分搜索树BST总结

1.二分搜索树特点

1. 是一棵二叉树。
2. 对于任意节点，如果节点的左子树不空，则左子树上所有结点的值均小于等于它的根结点的值； 如果节点的右子树不空，则右子树上所有结点的值均大于等于它的根结点的值

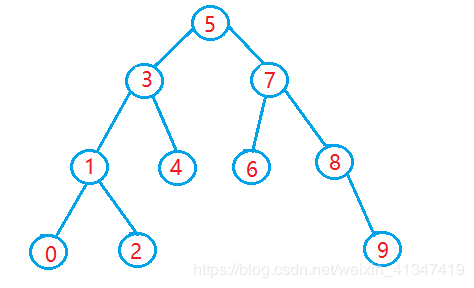
2.二叉搜索树的图例

例如：发现是不是符合我们上面说的两个特点，这就是二分搜索树，也叫二叉排序树。

3.二分搜索树优点

• 查找效率非常快 平均是O(lg n)级别

4. 二分搜索树缺点

在极端情况下会退化成线性结构，查找效率退化为O(n)级别

为什么？因为二分搜索树还可能长这样

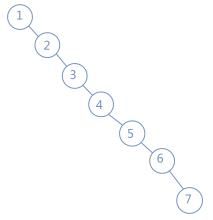
发现是不是也符合我们上面说的两个特点，不过这里左子树都为空而已。

5.二叉搜索树动态演示网站推荐

https://www.cs.usfca.edu/~galles/visualization/BST.html

6.如何构建二分搜索树？

构建二分搜索树无非就两个操作，添加元素和删除元素

6.1 添加元素

添加元素无非就是找到元素合适插入位置即可。怎么找？一棵二分搜索树本质上就“三个节点”，因为左子树，右子树也是一棵二分搜索树，即使为NULL。
如：

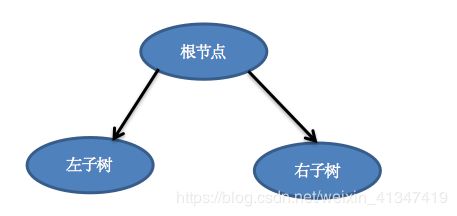
所有只有三个节点找到插入位置还不容易吗?
假如来了一个新节点，它比上图的右子树大，你觉得应该插在哪才符合二叉搜索树特点？
直接插到右子树的右孩子节点不就完事了么。 为什么？ 因为新节点先与根节点比较，发现新节点先比根节点大，如果根节点的右子树不为NULL于是新节点又和根节点的右子树比较（反之，新节点先比根节点小就和根节点的左子树比较），发现新节点先比根节点的右子树大，然后直接插到右子树的右孩子位置就行了。

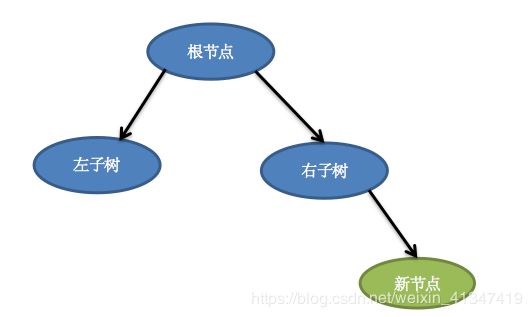
要是新节点小于右子树呢？插右子树的左孩子位置不就完事了么
因为新节点先与根节点比较，发现新节点先比根节点大，于是新节点又和根节点的右子树比较，发现新节点先比根节点的右子树小，然后直接插到右子树的左孩子位置就行了。

图片会插，那代码怎么实现？

/**
	
    递归语意： 向根节点为node的二叉搜索树添加元素e,并返回此二叉搜索树
 */
    private Node addNode(Node node,E e){
		
        if (node == null){
            this.size++;
            return new Node(e);
        }
  		//新节点比’根节点‘小，递归去左子树寻找插入位置
        if (e.compareTo(node.e) <0)
            node.left = addNode(node.left,e);
        //新节点比’根节点‘大，递归去右子树寻找插入位置
        else if (e.compareTo(node.e) > 0)
            node.right = addNode(node.right,e);

        //插入完成后返回此新的二叉树
        return node;

    }

6.2 删除操作

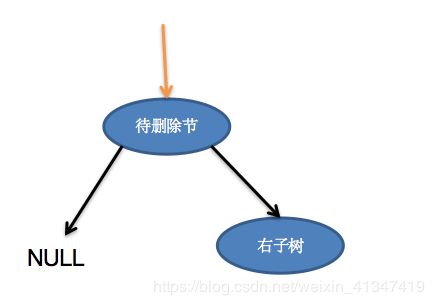
删除节点，首先得找到待删除节点，我们找到的待删除节点一定是下面这样子，黄色指针指向待删除节点的树。我们说了一棵树本质上就“三个节点”，即使左右子树都为NULL

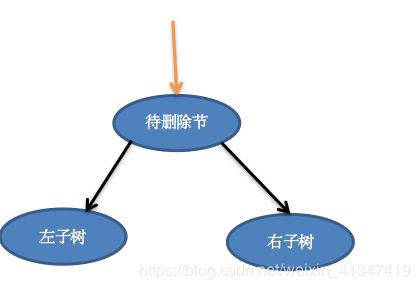
这时候待删除节点的删除实际上无非有三种情况：

1. 待删除节点的左子树为NULL

所以怎么删除？

• 直接让黄色指针指向右子树即可。
  
  这样就删除了？是的，因为上面的节点是靠黄色指针连接下面的树的。
  这段操作对应完整代码中的部分：

			 // 待删除节点左子树为空的情况
            if (node.left == null){
                Node right = node.right;
                node.right = null;
                this.size--;
                return  right;
            }

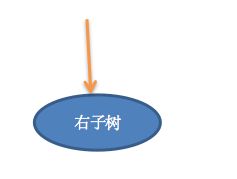
2. 待删除节点的右子树为NULL

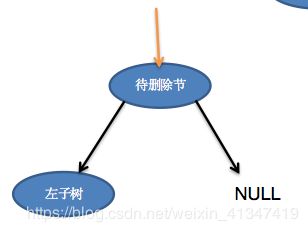
同1一样，直接让黄色指针指向左子树即可。

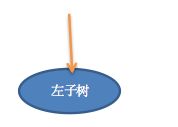
这段操作对应完整代码中的部分：

			 // 待删除节点右子树为空的情况
            if (node.right == null){
                Node  left = node.left;
                node.left = null;
                this.size--;
                return left;
            }

3. 待删除节点的左，右子树均存在

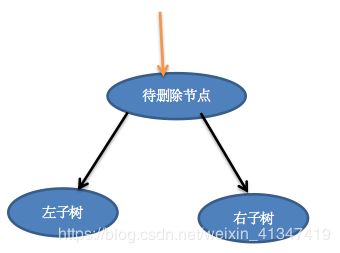
所以怎么删除？
找到待删除节点的右子树中最小的节点minNode，然后把待删除节点的值替换成minNode的值，再删除minNode节点。

来个图例吧：
我们放大视野来看一下右子树的内部，假设右子树只有三个节点，这时right为刚才右子树的根节点，T1为right的左孩子，T2为right的右孩子。

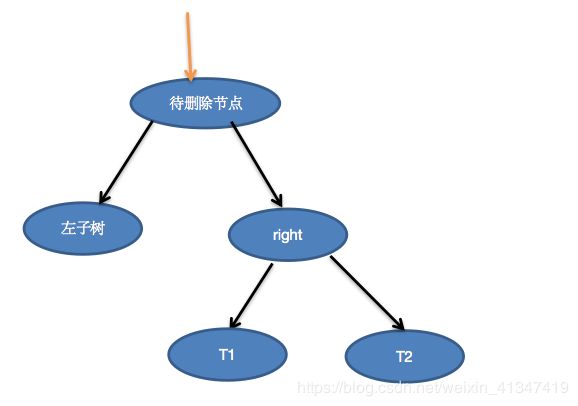
这时右子树的最小节点就是T1，我们让T1节点的值设置给待删除节点的值，然后再把right节点的左指针指向为NULL即可实现删除。

这段操作对应完整代码中的部分：

		// 待删除节点右子树为空的情况
        Node minNode = findMinimum(node.right); //找到待删除节点的右子树中最小的节点
        node.e = minNode.e;  //把minNode的值复制给待删除节点的值
        node.right = removeMinNode(node.right); //删除minNode
        return node;   //返回删除成功后的新的树的根节点

7. 二叉搜索树的遍历

我们说了本质上从最顶层视野来看 树只有三个节点，如下。所以我们遍历它的顺序会有四种，所以下面直接给出各种遍历输出的结果是怎样的

7.1 前序遍历（根左右）

遍历顺序为：根节点的值->左子树的值->右子树的值
⚠️：左子树的值再递归执行前序遍历即可。右子树同理，下面也同理

7.2 中序遍历（左根右）

遍历顺序为：左子树的值->根节点的值->右子树的值

7.3 后序遍历 （左右根）

遍历顺序为：左子树的值->右子树的值->根节点的值

7.1 层序遍历

遍历顺序为：第一层的值->第二层的值->第三层的值。。。以此类推
层序遍历就是一层一层遍历：
比如：

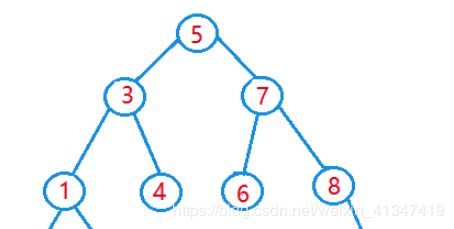
遍历顺序为：5->3->7->1->4->6->8

8.完整实现代码

public class BSTree<E extends Comparable<E>> {

    /**
     *   节点
     */
    private class Node {
        public E e;
        public Node left, right; //指向左右孩子

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;  //根节点
    private int size;  //树节点个数


    public BSTree() {
        this.root = null;
        this.size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }


    /**
     *      添加元素
     */
    public void add(E e){
        root = addNode(root, e);
    }
    //添加元素内部实现     递归语意： 向根节点为node的二叉搜索树添加元素e,并返回此二叉搜索树
    private Node addNode(Node node,E e){

        if (node == null){
            this.size++;
            return new Node(e);
        }

        if (e.compareTo(node.e) <0)
            node.left = addNode(node.left,e);
        else if (e.compareTo(node.e) > 0)
            node.right = addNode(node.right,e);

        //插入完成后返回此二叉树
        return node;

    }



    //判断二分搜索树中是否包含元素e对外接口
    public boolean contains(E e){
        return containsNode(root, e);
    }
    //递归语意：  判断以根节点为node的二叉搜索树是否包含元素e,并返回结果.
    private boolean containsNode(Node node,E e){
        //判断根节点
        if(node == null)
            return false;

        //判断根
        if(e.compareTo(node.e) == 0)
           return true;
        else if(e.compareTo(node.e) < 0)
            return containsNode(node.left,e);
        //判断右子树
        else //(e.compareTo(node.e) > 0)
            return containsNode(node.right,e);
    }


    /**
     *     遍历
     */
    //前序遍历
    public void preOrder(){
        preTraversing(root);
    }
    private void preTraversing(Node node){
        if(node == null)
            return;

        //遍历根节点
        System.out.println(node.e);
        //遍历左子树
        preTraversing(node.left);
        //遍历右子树
        preTraversing(node.right);
    }

    //中序遍历
    public void inOrder(){
        inTraversing(root);
    }
    private void inTraversing(Node node){
        if(node == null)
            return;
        //遍历左子树
        inTraversing(node.left);
        //遍历根节点
        System.out.println(node.e);
        //遍历右子树
        inTraversing(node.right);
    }

    //后序遍历
    public void postOrder(){
        postTraversing(root);
    }
    private void postTraversing(Node node){
        if(node == null)
            return;
        //遍历左子树
        postTraversing(node.left);
        //遍历右子树
        postTraversing(node.right);
        //遍历根节点
        System.out.println(node.e);
    }

    //层序遍历(广度优先遍历)
    public void levelOrder(){
        if (root == null)
            return;

        Queue<Node> queue = new ArrayDeque<>();
        queue.add(root);

        //出队一个节点后把与它连接的节点按顺序入队即可实现广度优先遍历
        while(!queue.isEmpty()){
            Node cur = queue.remove();

            System.out.println(cur.e);

            if (cur.left != null)
                queue.add(cur.left);

            if (cur.right != null)
                queue.add(cur.right);
        }
    }


    /**
     *   查找元素
     */
    // 寻找二分搜索树的最小元素
    public E minimum() {
        if(size == 0)
            throw new IllegalArgumentException("BST is empty");

        return findMinimum(root).e;
    }
    private Node findMinimum(Node node){
        //查找根节点为node的二叉搜索树的最小节点
        if( node.left == null )
            return node;
        return findMinimum(node.left);
    }

    // 寻找二分搜索树的最大元素
    public E maximum() {
        if(size == 0)
            throw new IllegalArgumentException("BST is empty");

        return findMaximum(root).e;

    }
    private Node findMaximum(Node node){
        //查找根节点为node的二叉搜索树的最大节点
        if(node.right == null)
            return node;

        return findMaximum(node.right);
    }


    /**
     *   删除节点
     */
    //删除最小的节点
    public E removeMin() {
        E res = minimum();
        root = removeMinNode(root);
        return res;
    }
    //删除以node为根节点的二叉搜索树的最小节点，并返回新的二叉树
    private Node removeMinNode(Node node) {
        //无左子树
        if (node.left == null){
            Node right  = node.right;
            node.right = null;
            this.size--;
            return right;
        }

        //有左子树
        node.left = removeMinNode(node.left);
        return node;
    }



    //删除最大所在节点
    public E removeMax(){
        E ret = maximum();
        root = removeMaxNode(root);
        return ret;
    }
    //删除以node为根节点的二叉搜索树的最大节点，并返回新的二叉树
    private Node removeMaxNode(Node node) {
        //无右子树
        if (node.right == null){
            Node left = node.left;
            node.left = null;
            this.size--;
            return left;
        }

        //有右子树
        node.right = removeMaxNode(node.right);
        return node;
    }



    //删除值为e的节点
    public void remove(E e){
        root = removeNode(root, e);
    }
    // 删除掉以node为根的二分搜索树中值为e的节点,返回删除节点后新的二分搜索树的根
    private Node removeNode(Node node, E e) {
        if( node == null )
            return null;

        // 找到待删除节点位置再删除
        if( e.compareTo(node.e) < 0 ){
            node.left = removeNode(node.left , e);
            return node;
        }
        else if(e.compareTo(node.e) > 0 ){
            node.right = removeNode(node.right, e);
            return node;
        }else {
            // 待删除节点左子树为空的情况
            if (node.left == null){
                Node right = node.right;
                node.right = null;
                this.size--;
                return  right;
            }

            // 待删除节点右子树为空的情况
            if (node.right == null){
                Node  left = node.left;
                node.left = null;
                this.size--;
                return left;
            }

            /** 核心：
             *       找到待删除节点delNode的右子树中最小的节点minNode
             *       然后把minNode的值和delNode的值替换，再删除minNode节点 用;
             * */
            Node minNode = findMinimum(node.right);
            node.e = minNode.e;
            node.right = removeMinNode(node.right);
            return node;
        }
    }
}

赞赏

如果觉得文章有用,你可鼓励下作者 如果浪费你时间了,在这里先跟你抱歉

---