蚁群算法总结

蚁群算法简介

蚁群算法（Ant Clony Optimization， ACO）是一种群智能算法，它是由一群无智能或有轻微智能的个体（Agent）通过相互协作而表现出智能行为，从而为求解复杂问题提供了一个新的方法。
蚁群算法是一种模拟进化算法，初步的研究表明该算法具有许多优良的性质。

蚁群算法最早用来求解TSP问题，并且表现出了很大的优越性，因为它分布式特性，鲁棒性强并且容易与其它算法结合，但是同时也存在这收敛速度慢，容易陷入局部最优（local optimal）等缺点。

蚂蚁寻找食物

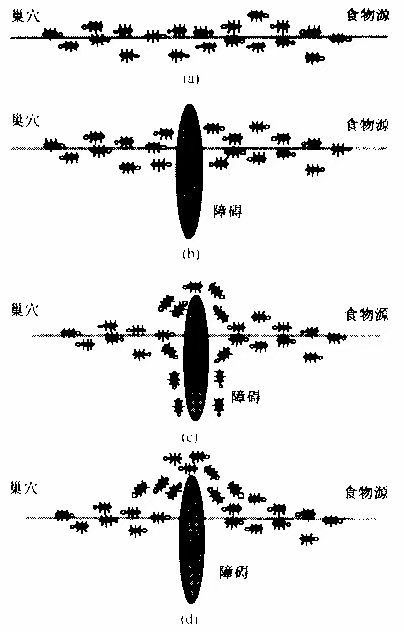
蚂蚁在行走过程中会释放一种称为“信息素”的物质，用来标识自己的行走路径。在寻找食物的过程中，根据信息素的浓度选择行走的方向，并最终到达食物所在的地方。

而信息素会随着时间的推移而逐渐挥发，所以在一开始的时候，由于地面上没有信息素，因此蚂蚁们的行走路径是随机的。蚂蚁们在行走的过程中会不断释放信息素，标识自己的行走路径。随着时间的推移，有若干只蚂蚁找到了食物，此时便存在若干条从洞穴到食物的路径。由于蚂蚁的行为轨迹是随机分布的，因此在单位时间内，短路径上的蚂蚁数量比长路径上的蚂蚁数量要多，从而蚂蚁留下的信息素浓度也就越高。这为后面的蚂蚁们提供了强有力的方向指引，越来越多的蚂蚁聚集到最短的路径上去。

优化问题与蚂蚁寻找食物的关系

蚁群算法	自然界的蚂蚁
可行解	蚂蚁行走的路径
最优解	待寻找的最短路径
解空间	所有可能的路径
信息素矩阵	某条途径上的信息素浓度
轮盘赌选择路径	根据信息素浓度来选择路径

蚁群算法基本操作

初始化参数

蚁群算法所需要的参数：

• 蚁群规模（蚂蚁数量）$m$
• 信息素重要程度因子 $\alpha$
• 启发函数重要程度因子 $\beta$
• 信息素挥发因子 $\rho$
• 信息素释放总量 $Q$
• 最大迭代次数 $ite{r}_{max}$

另外，设节点i与节点j之间的距离（权）为$d_{ij}(i,j=1,2,...,n)$，$t$时刻节点i与节点j连接路径上的信息素浓度为${\tau }_{ij}(t)$，在初始时刻各路径上信息素浓度相同，即${\tau }_{ij}(0)={\tau }_0$。

构建解空间

• 随机将蚂蚁置于所有出发点
• 蚂蚁按规则访问所有节点
• 计算每个蚂蚁经过的路径和长度，求出最优路径

访问规则：蚂蚁$k(k=1,2,...,m)$根据各个节点连接路径上的信息素浓度和路径距离（权）决定其下一个要访问的节点。t时刻蚂蚁k从节点i访问节点j的概率（蚂蚁已经在节点i）为：

$$P_{ij}^k=\frac{[{\tau }_{ij}(t){]}^{\alpha }\ast [{\eta }_{ij}(t){]}^{\beta }}{{\sum }_{s\in allo{w}_k}[{\tau }_{ij}(t){]}^{\alpha }\ast [{\eta }_{ij}(t){]}^{\beta }}s\in allo{w}_k$$
其中${\eta }_{ij}$为启发函数，${\eta }_{ij}=\frac{1}{d_{ij}}$，表示蚂蚁从节点i转移到节点j的期望程度；$allo{w}_k$表示蚂蚁k剩余待访问的节点集合。

更新信息素

蚂蚁访问完所有城市之后，进行信息素的更新。信息素的更新包括挥发和蚂蚁的产生，由以下公式决定：

$${\tau }_{ij}(t+1)=(1-\rho ){\tau }_{ij}(t)+\Delta {\tau }_{ij}$$

前一部分是信息素的挥发，后一部分表示每只蚂蚁在这一段路上新差生的信息素。

$$\Delta {\tau }_{ij}=\sum _{k=1}^n\Delta {\tau }_{ij}^k$$
即对每只蚂蚁在该段路上释放信息素浓度之和。而对于蚂蚁k在i到j之间所释放的信息素$\Delta {\tau }_{ij}^k$的计算，有三种不同的模型：

• 蚁周模型：释放总量一定，利用路径整体信息计算：（$L_k$为第k只蚂蚁经过路径的总长）
  $$\Delta {\tau }_{ij}^k=\frac{Q}{L_k}$$
• 蚁量模型：释放总量一定，利用路径局部信息计算：
  $$\Delta {\tau }_{ij}^k=\frac{Q}{d_{ij}}$$
• 蚁密模型：每段路释放量一定：
  $$\Delta {\tau }_{ij}^k=Q$$

判断终止与迭代

递增迭代次数计数器，如果达到了最大代数则输出，否则清空路径记录表继续迭代。

代码实现

代码使用蚁群算法计算中国TSP问题的最优解。

% 使用蚁群算法解决旅行商（TSP）问题的优化
% 中国31个省会城市的坐标数据保存在文件city_data.mat中

%导入数据
load city_data.mat

%计算城市之间的相互距离矩阵
n = size(city_data,1); %城市数目为n
D = zeros(n,n); %距离矩阵为D
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt((city_data(i,1)-city_data(j,1))^2+(city_data(i,2)-city_data(j,2))^2);
        else
            D(i,j) = 1e-4; %为了不使启发函数变成inf
        end
    end
end

%初始化蚁群算法各个参数
eta = 1./D; %启发函数
m = 31; %蚂蚁个数31
alpha = 1; %信息素重要程度因子
beta = 5; %启发函数重要程度因子
rho = 0.5; %信息素挥发因子
Q = 1; %信息素释放总量
iter_max = 400; %最大迭代次数
iter = 0; %代数初值
Table = zeros(m,n); %每只蚂蚁的路径记录表
tau = ones(n,n); %各节点间路径上的信息素含量记录表（tau0 = 1)

%开始迭代
while 1
    
    %结束迭代的条件
    iter = iter + 1;
    if iter >= iter_max
        break
    end
    
    %清空路径记录表
    Table = zeros(m,n);
    
    %构建解空间
    city = 1:n;
    
    %随机将蚂蚁置于所有出发点
    start = floor(n*rand(m,1))+1;
    Table(:,1) = start;
    
    %逐个蚂蚁进行路径选择
    for i = 1:m
        %对于每个蚂蚁，逐个节点进行访问
        for j = 2:n
            %初始化以访问的节点（禁忌表）
            tabu = Table(i,1:(j-1));
            allow = city(~ismember(city,tabu));
            %计算节点间转移概率
            P = zeros(size(allow));
            for k = 1:length(allow)
                P(k) = tau(tabu(end),allow(k))^alpha * eta(tabu(end),allow(k))^beta;
            end
            P = P/sum(P);
            %轮盘赌法选择下一个访问的城市
            P_sum = cumsum(P);
            target = allow(find(P_sum >= rand,1));
            Table(i,j) = target;
        end
    end
    
    %计算每个蚂蚁经过的路径
    Length = zeros(m,1);
    for i = 1:m
        Route = Table(i,:);
        for j = 1:(n-1)
            Length(i) = Length(i) + D(Route(j),Route(j+1));
        end
        Length(i) = Length(i) + D(Route(n),Route(1));
    end
    
    %更新信息素
    Delta_tau = zeros(n,n);
    for i = 1:m
        for j = 1:(n-1)
            Delta_tau(Table(i,j),Table(i,j+1)) = Delta_tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
        end
        Delta_tau(Table(i,n),Table(i,1)) = Delta_tau(Table(i,n),Table(i,1)) + Q/Length(i);
    end
    tau = (1-rho)*tau + Delta_tau;
    
end

min(Length)

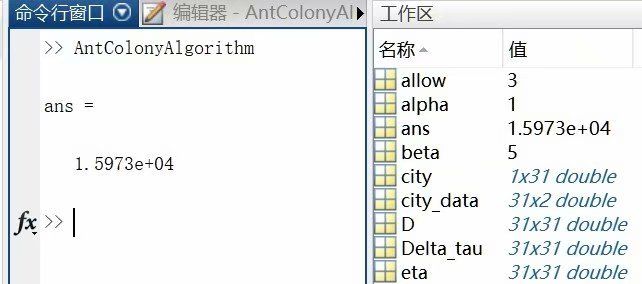
代码输出结果为：

而中国TSP问题的最新研究结果为15377km，因此该算法寻求到的是一个局部最优解。