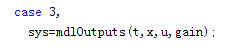Matlab S-function 使用总结
近期在学习电机的智能控制,里面用到了Matlab中的S函数,在此先对S-function做一个小结。
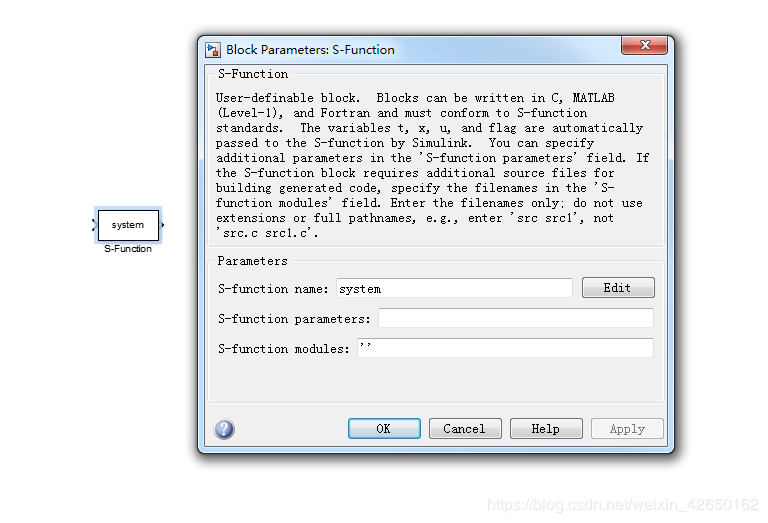
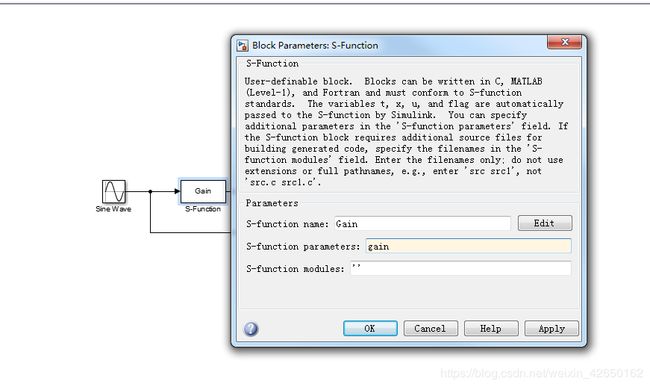
S-function模块,位于Simulink/User-Defined Functions模块库中,S-function模块及其对话框如下图所示:
S-function name:填入S-function的函数名称,这样就建立了S-function模块与M文件形式的S-function之间的对应关系,单机后面的Edit可以打开S-function的M文件的编辑窗口。
S-function parameters:填入S-function需要输入的外部参数的名称,如果有多个变量的话,中间用逗号隔开,如a,b,c.
S-function modules:只有S-function是用C语言编写并用MEX工具编译的C MEX文件时,才需要填写该参数。
设置完这些参数后,S-function模块就成为了一个具有指定功能的模块,它的功能取决于S-function的内容,也可对内容修改进而改变模块功能。
编写M文件S-function
在目录toolbol\simulink\blocks中给出了M文件S-function的模板sfuntmpl.m,我电脑上的路径如下图所示:
该模板由一个主函数和六个子函数组成,每个子函数对应一个特定的flag值。主函数通过flag的值分别调用不同的子函数。在仿真期间,这些子函数被S-function以回调程序的方式调用,执行S-function所需的任务。
学习S-function最直接有效的方法就是学习S-function范例,下面是我详细分析的sfuntmpl.m模板代码内容:
function [sys,x0,str,ts,simStateCompliance] = sfuntmpl(t,x,u,flag)
%主函数
%主函数包含四个输出:
% sys数组包含某个子函数返回的值
% x0为所有状态的初始化向量
% str是保留参数,总是一个空矩阵
% Ts返回系统采样时间
%函数的四个输入分别为采样时间t、状态x、输入u和仿真流程控制标志变量flag
%输入参数后面还可以接续一系列的附带参数simStateCompliance
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
%主函数结束
%下面是各个子函数,即各个回调过程
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
%初始化回调子函数
%提供状态、输入、输出、采样时间数目和初始状态的值
%初始化阶段,标志变量flag首先被置为0,S-function首次被调用时
%该子函数首先被调用,且为S-function模块提供下面信息
%该子函数必须存在
sizes = simsizes;
%生成sizes数据结构,信息被包含在其中
sizes.NumContStates = 0;
%连续状态数,缺省为0
sizes.NumDiscStates = 0;
%离散状态数,缺省为0
sizes.NumOutputs = 0;
%输出个数,缺省为0
sizes.NumInputs = 0;
%输入个数,缺省为0
sizes.DirFeedthrough = 1;
%是否存在直馈通道,1存在,0不存在
sizes.NumSampleTimes = 1;
%采样时间个数,至少是一个
sys = simsizes(sizes);
%返回size数据结构所包含的信息
x0 = [];
%设置初始状态
str = [];
%保留变量置空
ts = [0 0];
%设置采样时间
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
%计算导数回调子函数
%给定t,x,u计算连续状态的导数,可以在此给出系统的连续状态方程
%该子函数可以不存在
sys = [];
%sys表示状态导数,即dx
function sys=mdlUpdate(t,x,u)
%状态更新回调子函数
%给定t、x、u计算离散状态的更新
%每个仿真步内必然调用该子函数,不论是否有意义
%除了在此描述系统的离散状态方程外,还可以在此添加其他每个仿真步内都必须执行的代码
sys = [];
%sys表示下一个离散状态,即x(k+1)
function sys=mdlOutputs(t,x,u)
%计算输出回调函数
%给定t,x,u计算输出,可以在此描述系统的输出方程
%该子函数必须存在
sys = [];
%sys表示输出,即y
function sys=mdlGetTimeOfNextVarHit(t,x,u)
%计算下一个采样时间
%仅在系统是变采样时间系统时调用
sampleTime = 1;
%设置下一次采样时间是在1s以后
sys = t + sampleTime;
%sys表示下一个采样时间点
function sys=mdlTerminate(t,x,u)
%仿真结束时要调用的回调函数
%在仿真结束时,可以在此完成仿真结束所需的必要工作
sys = [];S-function应用实例
用S-function实现Gain增益模块,即对输入信号进行放大。
(1)首先将模板文件sfuntmpl.m另存为Gain.m,修改主函数,增加新的参数gain,修改函数名为Gain:
(2)增益参数是用来计算输出值的,所以需要对mdlOutput的调用进行修改:
(3)修改mdlInitializeSizes初始化回调子函数:
(4)修改mdlOutput输出子函数:
(5)保存Gain.m,并建立如下图所示的系统模型,对余弦信号的幅值放大gain倍。在S-function模块的参数对话框中设置S-function parameter 为3(该设置即为外部输入gain的大小)
完整代码如下所示:
function [sys,x0,str,ts,simStateCompliance] = Gain(t,x,u,flag,gain)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,gain);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [0 0];
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
sys = [];
function sys=mdlUpdate(t,x,u)
sys = [];
function sys=mdlOutputs(t,x,u,gain)
sys =gain*u;
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1;
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
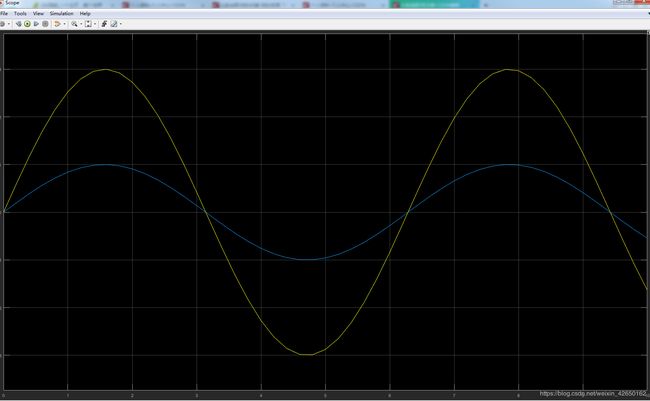
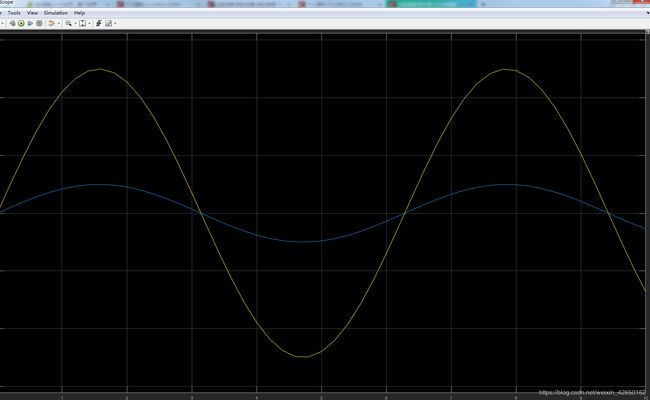
sys = [];(6)运行仿真,仿真结果如下图所示蓝线为输入,黄线为输出,输出放大了3(gain)倍。
注:在参数gain的设置时,为了更直观的表达可以对S-function模块进行封装
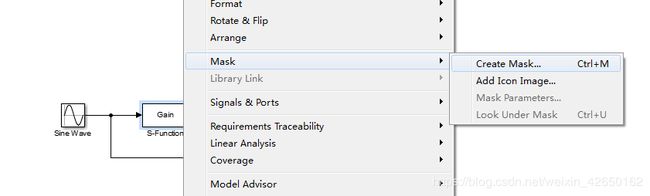
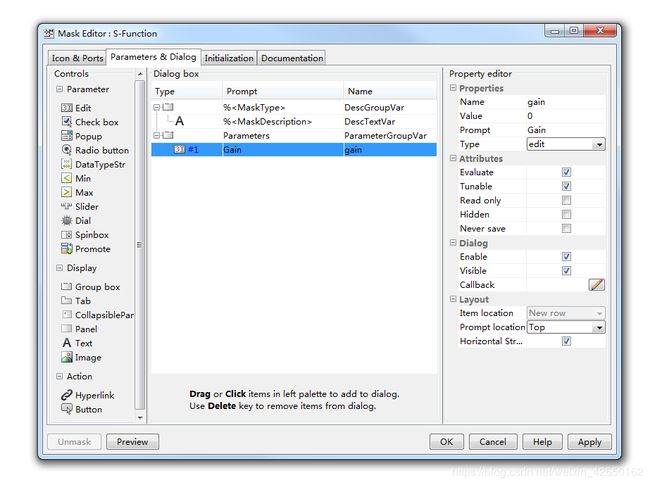
右击S-function模块,选择Mask,Creat Mask...对模块进行封装,如下图所示:
进行参数设置,如下图所示:
对S-function的S-function parameter 选项重新设置,如下图所示:
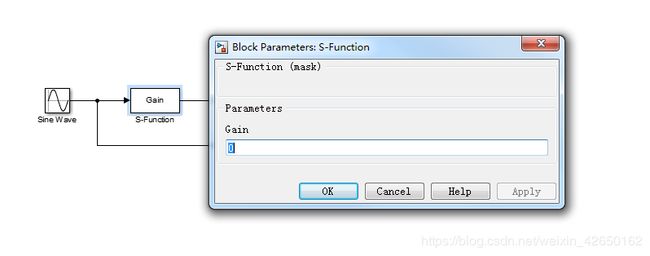
S-function parameter 的名称要和封装模块中的参数名称一样,此例中都为gain。都设置完成后再次点击S-function函数Gain会弹出如下参数设置框:
把增益gain设置为5,仿真结果如下:
这样可以更方便的对增益参数gain进行设置。
以上就是Matlab S-function 函数的使用心得,要用好S-function还是要多编几个程序,孰能生巧。S-function是Simulink最具魅力的地方,结合了Simulink框图简洁的特点和编程灵活的有点,增强和扩展了Sinulink的强大机制。