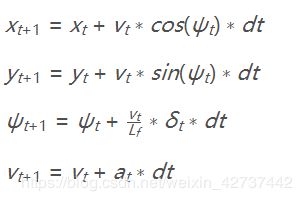自动驾驶中的模型预测控制(Model Predictive Control)
一、什么是模型预测控制(MPC)
MPC主要用于车道线的追踪,保持车辆轨迹相对平稳。
MPC将车道追踪任务重构成一个寻找最优解的问题,优化问题的最优解就是最优的轨迹。我们每走一步都会按照目前的状态求解一个最优化的轨迹,然后按照轨迹走一步,紧接着继续按照传感器获得的新值继续求解最优轨迹,保证轨迹跟 我们要追踪的车道线的最大拟合。这个过程中,因为我们每动一步,就是一个时间片段,因为各种误差的存在,导致我们的车辆并不能完全符合预测出来的轨迹,所以每一次都得重新计算调整。
二、车辆的模型
想要对车辆进行模型预测控制,首先我们得对车辆进行建模。这里我们对车辆的动力学模型进行一个简化,当然越复杂的模型预测起来就会更加准确,但是简单的模型更加方便计算和理解。
运动学模型
运动学模型忽略了轮胎力,重力以及质量,这种模型可以说是经过了极大的的简化,所以精确度低,但是因为经过简化,所以很好计算,而且在低中速的运动中还有这相当不错的精度
动力学模型
动力学模型是尽可能的体现出实际上车辆的动态。它计算到了轮胎的摩擦力,横向和纵向的加速度,惯性,中立,空气阻力,质量以及车辆的物理形状,所以不同的车的动力学模型很可能是不一样的,而且考虑的因素越多也就相对越精确。有的复杂的动力学模型甚至会考虑到底盘悬挂如何响应。
2.1 静态模型
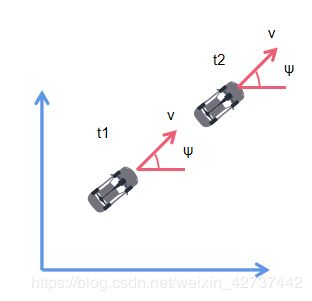
首先我们来描述一辆车的静态的状态,那么就有坐标x,y,然后车头会有一个跟参考方向的夹角ψ。

2.2 动态模型
如果汽车动起来,那么就会增加一个参数v,即速度:

所以我们汽车的状态向量就是
X = [x,y,ψ,v]
2.3 状态控制向量
我们想要控制汽车的动作,需要通过方向盘和油门踏板来实现,这里我们简化一下,把这两个都看作是单独的执行器。
δ代表方向的转动角度(注意不是方向盘的转角,而是车轮的偏向角);
a代表油门踏板的动作,正数为加速,负数为减速。
所以状态控制向量为:
[δ,a]
2.4 车道线的拟合
一般来说对于大多数道路,我们如果使用多项式拟合的话,那么三次多项式就足够在一定距离内比较好的拟合车道了。
2.5 各种公式
假设我们计算的时间间隔为Δt。
首先,针对位置信息x和y:

然后,对于偏向角ψ:

我们用到了转角加速度δ,然后Lf表示汽车的半轴长,与转弯半径相关,这个值越大,转弯半径越大。然后呢,当去读越快的时候,转弯速度也是最快的,所以速度也包含在内。
接下来就是速度:
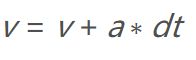
其中a为油门踏板了,取值为-1——1。
VectorXd globalKinematic(const VectorXd &state,
const VectorXd &actuators, double dt) {
// Create a new vector for the next state.
VectorXd next_state(state.size());
// state is [x, y, psi, v] and actuators is [delta, a]
double x_t = state(0);
double y_t = state(1);
double psi_t = state(2);
double v_t = state(3);
double delta_t = actuators(0);
double a_t = actuators(1);
double x = x_t + v_t * cos(psi_t) * dt;
double y = y_t + v_t * sin(psi_t) * dt;
double psi = psi_t + v_t / Lf * delta_t * dt;
double v = v_t + a_t * dt;
next_state << x,y,psi,v;
return next_state;
}
拟合三次曲线
#include 2.6 误差计算
我们通过将误差最小化作为调优的目标。
我们新的状态向量是 [x,y,ψ,v,cte,eψ].
2.6.1 航向偏差
航向偏差表示汽车的行进路线与道路中心线的偏差,
ctet+1=ctet+vt∗sin(eψt)∗dt
ctet可以表示为车辆当前位置与yt(道路中心线)之间的差值,所以有:
ctet=f(xt)−yt
然后带入上式可得:
ctet+1=f(xt)−yt+vt∗sin(eψt)∗dt
其中的误差可以分为两部分:
- f(xt)−yt为当前的航迹偏差
- vt∗sin(eψt)∗dt为车辆运动引起的偏差
2.6.2 方向偏差
接下来就是方向偏差:
![]()
计算方法跟ψ类似。
eψt的计算方法是使用eψt减去目标角度。
eψt = ψt - ψdest
ψt是已知的,但是ψdest是未知的,我们只知道路径的多项式,我们可以使用当前点的正切角来计算这个值,arctan(f′ (xt)),f′是轨迹的导数。
![]()
- eψt是当前的方向偏差
- 后部分是速度造成的偏差
三、MPC的实现
3.1 工具
这里我们用到两个工具,辅助我们的计算
3.1.1 Ipopt
ipopt是一个解决非线性规划最优化问题的工具集,当然,它也能够用于解决线性规划问题的求解。
ipopt可以根据我们的约束条件来求解局部最优,所以很适用与非线性问题。但是这个工具要求我们提供约束条件的Jacobian矩阵和目标函数的Hessian矩阵,这个其实还是比较费劲的,所以我们有了以下的工具:CppAD
3.1.2 CppAD
CppAD是一个自动计算导数的工具,
为了使用其计算导数,我们所有的计算函数以及数据类型都需要使用这个包里自带的。例如:
CppAD::pow(x, 2);
// instead of
pow(x, 2);
3.2 初始化
首先设置各种初始化的值
/**
* 设置时间间隔和预测的步数
*/
size_t N = 10;
double dt = 0.1;
//设置半轴长
const double Lf = 2.67;
//设置目标车速
double ref_v = 40.0;
// 定义每一个state的起始点,因为函数的需要,只能传入一个数组,所以将误差以及各种状态的点都放在一个数组中展开
size_t x_start = 0;
size_t y_start = x_start + N;
size_t psi_start = y_start + N;
size_t v_start = psi_start + N;
size_t cte_start = v_start + N;
size_t epsi_start = cte_start + N;
size_t delta_start = epsi_start + N;
size_t a_start = delta_start + N - 1;
3.3 设置约束
class FG_eval {
public:
// Fitted polynomial coefficients
VectorXd coeffs;
FG_eval(VectorXd coeffs) { this->coeffs = coeffs; }
typedef CPPAD_TESTVECTOR(AD<double>) ADvector;
void operator()(ADvector& fg, const ADvector& vars) {
// The cost is stored is the first element of `fg`.
// Any additions to the cost should be added to `fg[0]`.
fg[0] = 0;
// Reference State Cost
// 损失函数,目的是将损失函数降到最小,求最优化解
//基于参考状态的损失,求状态的最优化,最小的距离,最小的夹角,最小的速度
for (unsigned int i = 0; i < N; i++)
{
fg[0] += 500 * CppAD::pow(vars[cte_start + i], 2);
fg[0] += 500 * CppAD::pow(vars[epsi_start + i],2);
fg[0] += CppAD::pow(vars[v_start + i] - ref_v,2);
}
//执行器的损失,求执行器的最优化值
for (unsigned int i = 0; i < N - 1; i++)
{
fg[0] += 50 * CppAD::pow(vars[delta_start + i], 2);
fg[0] += 50 * CppAD::pow(vars[a_start + i],2);
// try adding penalty for speed + steer
// fg[0] += 700*CppAD::pow(vars[delta_start + i] * vars[v_start+i], 2);
}
// 求两次动作的最优化值
for (int i = 0; i < N - 2; i++) {
fg[0] += 200*CppAD::pow(vars[delta_start + i + 1] - vars[delta_start + i], 2);
fg[0] += 10*CppAD::pow(vars[a_start + i + 1] - vars[a_start + i], 2);
}
//
// Setup Constraints
// 设置约束,在这里设置约束条件
//
// Initial constraints
//
// We add 1 to each of the starting indices due to cost being located at
// index 0 of `fg`.
// This bumps up the position of all the other values.
//因为fg【0】是损失,其余的状态从fg【1】开始
fg[1 + x_start] = vars[x_start];
fg[1 + y_start] = vars[y_start];
fg[1 + psi_start] = vars[psi_start];
fg[1 + v_start] = vars[v_start];
fg[1 + cte_start] = vars[cte_start];
fg[1 + epsi_start] = vars[epsi_start];
// The rest of the constraints
for (int t = 1; t < N; ++t) {
//t时刻的状态值
AD<double> x1 = vars[x_start + t];
AD<double> y1 = vars[y_start + t];
AD<double> psi1 = vars[psi_start + t];
AD<double> v1 = vars[v_start + t];
AD<double> cte1 = vars[cte_start + t];
AD<double> epsi1 = vars[epsi_start + t];
//t-1时刻的状态
AD<double> x0 = vars[x_start + t - 1];
AD<double> y0 = vars[y_start + t - 1];
AD<double> psi0 = vars[psi_start + t - 1];
AD<double> v0 = vars[v_start + t - 1];
AD<double> cte0 = vars[cte_start + t - 1];
AD<double> epsi0 = vars[epsi_start + t - 1];
//只计算t-1时刻
AD<double> delta0 = vars[delta_start + t - 1];
AD<double> a0 = vars[a_start + t - 1];
if (t > 1) { // use previous actuations (to account for latency)
a0 = vars[a_start + t - 2];
delta0 = vars[delta_start + t - 2];
}
AD<double> f0 = coeffs[0] + coeffs[1] * x0 + coeffs[2] * CppAD::pow(x0, 2) + coeffs[3] * CppAD::pow(x0, 3);
AD<double> psides0 = CppAD::atan(coeffs[1] + 2 * coeffs[2] * x0 + 3 * coeffs[3] * CppAD::pow(x0, 2));
// The idea here is to constraint this value to be 0.
//
// NOTE: The use of `AD` and use of `CppAD`!
// CppAD can compute derivatives and pass these to the solver.
//约束条件,目的是让该值等于0 ,所以前一时刻的状态经过变换应该等于下一时刻的状态
// x_[t+1] = x[t] + v[t] * cos(psi[t]) * dt
// y_[t+1] = y[t] + v[t] * sin(psi[t]) * dt
// psi_[t+1] = psi[t] + v[t] / Lf * delta[t] * dt
// v_[t+1] = v[t] + a[t] * dt
// cte[t+1] = f(x[t]) - y[t] + v[t] * sin(epsi[t]) * dt
// epsi[t+1] = psi[t] - psides[t] + v[t] * delta[t] / Lf * dt
fg[1 + x_start + t] = x1 - (x0 + v0 * CppAD::cos(psi0) * dt);
fg[1 + y_start + t] = y1 - (y0 + v0 * CppAD::sin(psi0) * dt);
fg[1 + psi_start + t] = psi1 - (psi0 - v0 * delta0 / Lf * dt);
fg[1 + v_start + t] = v1 - (v0 + a0 * dt);
fg[1 + cte_start + t] = cte1 - ((f0 - y0) + (v0 * CppAD::sin(epsi0) * dt));
fg[1 + epsi_start + t] = epsi1 - ((psi0 - psides0) + v0 * delta0 / Lf * dt);
}
}
};
3.4 根据约束求解最优解
std::vector<double> MPC::Solve(const VectorXd &state, const VectorXd &coeffs) {
bool ok = true;
typedef CPPAD_TESTVECTOR(double) Dvector;
double x = state[0];
double y = state[1];
double psi = state[2];
double v = state[3];
double cte = state[4];
double epsi = state[5];
/**
* Set the number of model variables (includes both states and inputs).
* For example: If the state is a 4 element vector, the actuators is a 2
* element vector and there are 10 timesteps. The number of variables is:
* 4 * 10 + 2 * 9
*/
// 独立变量的个数
// N timesteps == N - 1 actuations
size_t n_vars = state.size() * 10 + (N - 1) * 2;
/**
* 设置变量个数
*/
size_t n_constraints = N * 6;
// 初始化所有独立变量的值
// SHOULD BE 0 besides initial state.
Dvector vars(n_vars);
for (int i = 0; i < n_vars; ++i) {
vars[i] = 0.0;
}
// Set the initial variable values
//设置初始状态
vars[x_start] = x;
vars[y_start] = y;
vars[psi_start] = psi;
vars[v_start] = v;
vars[cte_start] = cte;
vars[epsi_start] = epsi;
/**
* TODO: Set lower and upper limits for variables.
*/
// Lower and upper limits for x
//所有x的极限值
Dvector vars_lowerbound(n_vars);
Dvector vars_upperbound(n_vars);
// Set all non-actuators upper and lowerlimits
// to the max negative and positive values.
//将所有非执行器的状态量的最大最小值分别都拉到最大
for (int i = 0; i < delta_start; ++i) {
vars_lowerbound[i] = -1.0e19;
vars_upperbound[i] = 1.0e19;
}
// The upper and lower limits of delta are set to -25 and 25
// degrees (values in radians).
//将所有的delta的限制设置为±25°
for (int i = delta_start; i < a_start; ++i) {
vars_lowerbound[i] = -0.436332;
vars_upperbound[i] = 0.436332;
}
// Acceleration/decceleration upper and lower limits.
// 加速/减速上限和下限。
for (int i = a_start; i < n_vars; ++i) {
vars_lowerbound[i] = -1.0;
vars_upperbound[i] = 1.0;
}
// Lower and upper limits for the constraints
// 约束的下限和上限
Dvector constraints_lowerbound(n_constraints);
Dvector constraints_upperbound(n_constraints);
for (int i = 0; i < n_constraints; ++i) {
constraints_lowerbound[i] = 0;
constraints_upperbound[i] = 0;
}
constraints_lowerbound[x_start] = x;
constraints_lowerbound[y_start] = y;
constraints_lowerbound[psi_start] = psi;
constraints_lowerbound[v_start] = v;
constraints_lowerbound[cte_start] = cte;
constraints_lowerbound[epsi_start] = epsi;
constraints_upperbound[x_start] = x;
constraints_upperbound[y_start] = y;
constraints_upperbound[psi_start] = psi;
constraints_upperbound[v_start] = v;
constraints_upperbound[cte_start] = cte;
constraints_upperbound[epsi_start] = epsi;
// object that computes objective and constraints
FG_eval fg_eval(coeffs);
// NOTE: You don't have to worry about these options
// options for IPOPT solver
std::string options;
// Uncomment this if you'd like more print information
options += "Integer print_level 0\n";
// NOTE: Setting sparse to true allows the solver to take advantage
// of sparse routines, this makes the computation MUCH FASTER. If you can
// uncomment 1 of these and see if it makes a difference or not but if you
// uncomment both the computation time should go up in orders of magnitude.
options += "Sparse true forward\n";
options += "Sparse true reverse\n";
// NOTE: Currently the solver has a maximum time limit of 0.5 seconds.
// Change this as you see fit.
options += "Numeric max_cpu_time 0.5\n";
// place to return solution
CppAD::ipopt::solve_result<Dvector> solution;
// solve the problem
CppAD::ipopt::solve<Dvector, FG_eval>(
options, vars, vars_lowerbound, vars_upperbound, constraints_lowerbound,
constraints_upperbound, fg_eval, solution);
// Check some of the solution values
ok &= solution.status == CppAD::ipopt::solve_result<Dvector>::success;
// Cost
auto cost = solution.obj_value;
std::cout << "Cost " << cost << std::endl;
/**
* TODO: Return the first actuator values. The variables can be accessed with
* `solution.x[i]`.
*
* {...} is shorthand for creating a vector, so auto x1 = {1.0,2.0}
* creates a 2 element double vector.
*/
std::vector<double> res;
res.push_back(solution.x[delta_start]);
res.push_back(solution.x[a_start]);
for (size_t i = 0; i < N - 2; i++)
{
res.push_back(solution.x[x_start + i + 1 ]);
res.push_back(solution.x[y_start + i + 1 ]);
}
return res;
}
3.5 转换坐标系
将世界坐标系转换为车辆坐标系
vector<double> ptsx = j[1]["ptsx"];
vector<double> ptsy = j[1]["ptsy"];
double px = j[1]["x"];
double py = j[1]["y"];
double psi = j[1]["psi"];
double v = j[1]["speed"];
assert(ptsx.size() == ptsy.size());
// 转化世界坐标系航点为车辆坐标系航点
vector<double> waypoints_x;
vector<double> waypoints_y;
for (int i = 0; i < ptsx.size(); i++)
{
double dx = ptsx[i] - px;
double dy = ptsy[i] - py;
waypoints_x.push_back(dx * cos(-psi) - dy * sin(-psi));
waypoints_y.push_back(dx * sin(-psi) + dy * cos(-psi));
}
//将指针赋值地址
double* ptrx = &waypoints_x[0];
double* ptry = &waypoints_y[0];
//使用指针来构建矩阵或向量,map是一个引用
Eigen::Map<Eigen::VectorXd> waypoints_mx(ptrx, 6);
Eigen::Map<Eigen::VectorXd> waypoints_my(ptry, 6);
四、PID和MPC
在真是的汽车中,我们的控制动作不会立即作用于系统中,往往有个迟滞,这个对于PID来说是个挑战,但是对于MPC,我们可以把这个迟滞添加到模型中。
4.1 PID
PID控制是计算目前状态的偏差,无法对未来进行预测,所以未来的状态对于汽车来说完全是未知的,汽车无法预测自己的动作对于未来的影响。
如果PID计算通过预测未来的偏差来计算控制量,系统也因为没有模型而无法准确控制。
MPC
MPC是动态的,考虑到了影响到了汽车动作的各种因素,所以可以很容易的将类似于迟滞这样的因素加入到模型中,更有利于我们精细的控制汽车。
五、完整代码
完整代码见我的github