深度学习基础1:神经网络反向传播(BackPropagation, BP)算法
目录
- 链式求导法则
- 神经网络结构
- 神经网络前向传播
- 反向传播的网络结构
- 神经网络反向传播推导
- 偏置
链式求导法则
方程1. f ( x , y ) = 0 f(x,y)=0 f(x,y)=0
方程2. g ( x , y ) = 0 g(x,y)=0 g(x,y)=0
方程3. z ( f , g ) = 0 z(f,g)=0 z(f,g)=0
计算 z z z对 x , y x,y x,y的偏导:
∂ z ∂ x = ∂ z ∂ f ∗ ∂ f ∂ x + ∂ z ∂ g ∗ ∂ g ∂ x \frac{\partial z}{\partial x}=\frac{\partial z}{\partial f}*\frac{\partial f}{\partial x}+\frac{\partial z}{\partial g}*\frac{\partial g}{\partial x} ∂x∂z=∂f∂z∗∂x∂f+∂g∂z∗∂x∂g
∂ z ∂ y = ∂ z ∂ f ∗ ∂ f ∂ y + ∂ z ∂ g ∗ ∂ g ∂ y \frac{\partial z}{\partial y}=\frac{\partial z}{\partial f}*\frac{\partial f}{\partial y}+\frac{\partial z}{\partial g}*\frac{\partial g}{\partial y} ∂y∂z=∂f∂z∗∂y∂f+∂g∂z∗∂y∂g
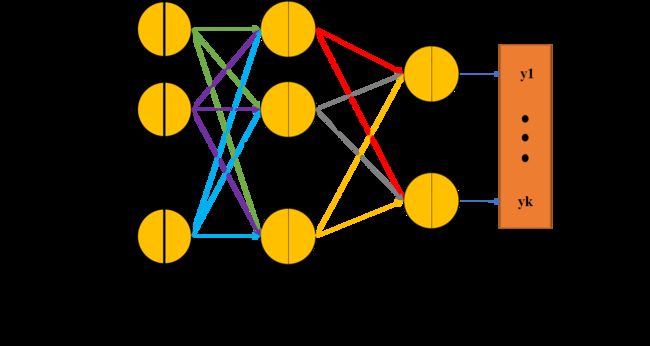
神经网络结构
| 符号 | 意义 |
|---|---|
| X | 训练数据 |
| Y | 训练标签(目标值) |
| 1…M;1…N | 隐藏层 j, k 的神经元序号 |
| 1…T | 输出层神经元序号 |
| N e t m j Net_m^j Netmj | 网络层j的第 m m m个神经元的输入(节点输入) |
| H m j H_m^j Hmj | 网络层 j j j的第 m m m个神经元的输出 (节点输出) |
| f ( . ) f(.) f(.) | 激活函数 |
| W n , m j W_{n,m}^j Wn,mj | 网络层 j j j第 m m m个神经元输入到网络层 j + 1 j+1 j+1第 n n n个神经元的权重 |
| δ m j \delta_m^j δmj | 网络层 j j j第 m m m个神经元的输出偏差(残差) |
| η \eta η | 梯度下降的步长 |
神经网络前向传播
- 输出层第t个神经元的输出 H t 4 H_t^4 Ht4:
H t 4 = f ( N e t t 4 ) H_t^4=f(Net_t^4) Ht4=f(Nett4)---------------------------------------------- 第四层输出-----------(1)
N e t t 4 = ∑ n = 1 N ( W t , n 3 ∗ H n 3 ) Net_t^4=\sum_{n=1}^N(W_{t,n}^3*H_n^3) Nett4=∑n=1N(Wt,n3∗Hn3)---------------------------- 第四层输入------------(2)
H n 3 = f ( N e t n 3 ) H_n^3=f(Net_n^3) Hn3=f(Netn3), for n = 1 , . . . , N n = 1,...,N n=1,...,N--------------------- 第三层输出------------(3)
N e t n 3 = ∑ m = 1 M W n , m 2 ∗ H m 2 Net_n^3=\sum_{m=1}^MW^2_{n,m}*H^2_m Netn3=∑m=1MWn,m2∗Hm2, for n = 1 , . . . , N n = 1,...,N n=1,...,N---- 第三层输入------------(4)
H m 2 = f ( N e t m 2 ) H^2_m=f(Net^2_m) Hm2=f(Netm2), for m = 1 , . . . , M m = 1,...,M m=1,...,M------------------ 第二层输出------------(5)
N e t m 2 = W m , 1 1 ∗ X 1 + W m , 2 1 ∗ X 2 Net^2_m=W^1_{m,1}*X1+W^1_{m,2}*X2 Netm2=Wm,11∗X1+Wm,21∗X2------------------- 第二层输入-----------(6)
第一层输入输出均为: [ X 1 , X 2 ] T [X1,X2]^T [X1,X2]T------------------------ 第一层:输入层------(7)
以上即为输出层第一个神经元 H 1 4 H_1^4 H14的传播过程
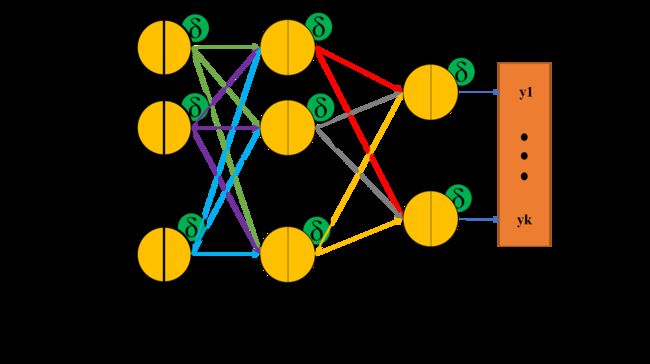
反向传播的网络结构
神经网络反向传播推导
- 首先我们看一下网络的代价函数,其实就是:
%% 计算(目标值减去最后一层网络的输出值)的模的平方
(8) L o s s = 1 2 ∗ ∣ ∣ Y − H 4 ∣ ∣ 2 2 = 1 2 ∗ ∑ t = 1 T ( y t − H t 4 ) 2 \begin{aligned} Loss &= \frac{1}{2}*||Y-H^4||_2^2\\ &=\frac{1}{2}*\sum^T_{t=1}(y_t-H^4_t)^2\tag{8} \end{aligned} Loss=21∗∣∣Y−H4∣∣22=21∗t=1∑T(yt−Ht4)2(8) - 将公式(1)(2)代入(8)
(9) L o s s = 1 2 ∗ ∑ t = 1 T ( y t − f ( N e t t 4 ) ) 2 = 1 2 ∗ ∑ t = 1 T ( y t − f ( ∑ n = 1 N W t , n 3 ∗ H n 3 ) ) 2 = 1 2 ∗ ∑ t = 1 T ( y t − f ( ∑ n = 1 N W t , n 3 ∗ f ( N e t n 3 ) ) ) 2 = . . . . . . \begin{aligned} Loss &= \frac{1}{2}*\sum^T_{t=1}(y_t-f(Net^4_t))^2\\ &=\frac{1}{2}*\sum^T_{t=1}(y_t-f(\sum_{n=1}^NW_{t,n}^3*H_n^3))^2\\ &=\frac{1}{2}*\sum^T_{t=1}(y_t-f(\sum_{n=1}^NW_{t,n}^3*f(Net_n^3)))^2\\ &=......\tag{9} \end{aligned} Loss=21∗t=1∑T(yt−f(Nett4))2=21∗t=1∑T(yt−f(n=1∑NWt,n3∗Hn3))2=21∗t=1∑T(yt−f(n=1∑NWt,n3∗f(Netn3)))2=......(9) - 计算导数 L o s s Loss Loss对第三层网络权重的倒数:
(10) ∂ L o s s ∂ W t , n 3 = ∂ L o s s ∂ N e t t 4 ∗ ∂ N e t t 4 ∂ W t , n 3 \begin{aligned} \frac{\partial{Loss}}{\partial{W^3_{t,n}}}=\frac{\partial{Loss}}{\partial{Net^4_t}}*\frac{\partial{Net^4_t}}{\partial{W^3_{t,n}}}\tag{10} \end{aligned} ∂Wt,n3∂Loss=∂Nett4∂Loss∗∂Wt,n3∂Nett4(10)
(11) ∂ L o s s ∂ W n , m 2 = ∂ L o s s ∂ N e t n 3 ∗ ∂ N e t n 3 ∂ W n , m 2 \begin{aligned} \frac{\partial{Loss}}{\partial{W^2_{n,m}}}=\frac{\partial{Loss}}{\partial{Net_n^3}}*\frac{\partial{Net_n^3}}{\partial{W^2_{n,m}}}\tag{11} \end{aligned} ∂Wn,m2∂Loss=∂Netn3∂Loss∗∂Wn,m2∂Netn3(11)
(12) ∂ L o s s ∂ W m , i 1 = ∂ L o s s ∂ N e t n 2 ∗ ∂ N e t n 2 ∂ W m , i 1 \begin{aligned} \frac{\partial{Loss}}{\partial{W^1_{m,i}}}=\frac{\partial{Loss}}{\partial{Net_n^2}}*\frac{\partial{Net_n^2}}{\partial{W^1_{m,i}}}\tag{12} \end{aligned} ∂Wm,i1∂Loss=∂Netn2∂Loss∗∂Wm,i1∂Netn2(12)
令 δ t 4 = − ∂ L o s s ∂ N e t t 4 \delta^4_t=-\frac{\partial{Loss}}{\partial{Net^4_t}} δt4=−∂Nett4∂Loss, δ n 3 = − ∂ L o s s ∂ N e t n 3 \delta^3_n=-\frac{\partial{Loss}}{\partial{Net^3_n}} δn3=−∂Netn3∂Loss, δ m 2 = − ∂ L o s s ∂ N e t m 2 \delta^2_m=-\frac{\partial{Loss}}{\partial{Net^2_m}} δm2=−∂Netm2∂Loss
3.1. 下面计算权重增量:
(13) Δ W t , n 3 = − η ∗ ∂ L o s s ∂ W t , n 3 = − η ∗ ∂ L o s s ∂ N e t t 4 ∗ ∂ N e t t 4 ∂ W t , n 3 = η ∗ δ t 4 ∗ ∂ N e t t 4 ∂ W t , n 3 \begin{aligned} \Delta{W^3_{t,n}}=-\eta*\frac{\partial{Loss}}{\partial{W^3_{t,n}}}=-\eta*\frac{\partial{Loss}}{\partial{Net^4_t}}*\frac{\partial{Net^4_t}}{\partial{W^3_{t,n}}}=\eta*\delta^4_t*\frac{\partial{Net^4_t}}{\partial{W^3_{t,n}}}\tag{13} \end{aligned} ΔWt,n3=−η∗∂Wt,n3∂Loss=−η∗∂Nett4∂Loss∗∂Wt,n3∂Nett4=η∗δt4∗∂Wt,n3∂Nett4(13)
(14) Δ W n , m 2 = − η ∗ ∂ L o s s ∂ W n , m 2 = − η ∗ ∂ L o s s ∂ N e t n 3 ∗ ∂ N e t n 3 ∂ W n , m 2 = η ∗ δ n 3 ∗ ∂ N e t n 3 ∂ W n , m 2 \begin{aligned} \Delta{W^2_{n,m}}=-\eta*\frac{\partial{Loss}}{\partial{W^2_{n,m}}}=-\eta*\frac{\partial{Loss}}{\partial{Net^3_n}}*\frac{\partial{Net^3_n}}{\partial{W^2_{n,m}}}=\eta*\delta^3_n*\frac{\partial{Net^3_n}}{\partial{W^2_{n,m}}}\tag{14} \end{aligned} ΔWn,m2=−η∗∂Wn,m2∂Loss=−η∗∂Netn3∂Loss∗∂Wn,m2∂Netn3=η∗δn3∗∂Wn,m2∂Netn3(14)
(15) Δ W m , i 1 = − η ∗ ∂ L o s s ∂ W m , i 1 = − η ∗ ∂ L o s s ∂ N e t m 2 ∗ ∂ N e t m 2 ∂ W m , i 1 = η ∗ δ m 2 ∗ ∂ N e t m 2 ∂ W m , i 1 \begin{aligned} \Delta{W^1_{m,i}}=-\eta*\frac{\partial{Loss}}{\partial{W^1_{m,i}}}=-\eta*\frac{\partial{Loss}}{\partial{Net^2_m}}*\frac{\partial{Net^2_m}}{\partial{W^1_{m,i}}}=\eta*\delta^2_m*\frac{\partial{Net^2_m}}{\partial{W^1_{m,i}}}\tag{15} \end{aligned} ΔWm,i1=−η∗∂Wm,i1∂Loss=−η∗∂Netm2∂Loss∗∂Wm,i1∂Netm2=η∗δm2∗∂Wm,i1∂Netm2(15)
3.2. 下面分别计算 δ t 4 , δ n 3 , δ m 2 \delta^4_t,\delta^3_n,\delta^2_m δt4,δn3,δm2
(16) δ t 4 = − ∂ L o s s ∂ N e t t 4 = ( y t − H t 4 ) ∗ f ′ ( N e t t 4 ) \begin{aligned} \delta^4_t=-\frac{\partial{Loss}}{\partial{Net^4_t}}=(y_t-H^4_t)*f'(Net^4_t)\tag{16} \end{aligned} δt4=−∂Nett4∂Loss=(yt−Ht4)∗f′(Nett4)(16)
(17) δ n 3 = − ∂ L o s s ∂ N e t n 3 = ∑ t = 1 T ( y t − H t 4 ) ∗ f ′ ( N e t t 4 ) ∗ W t , n 3 ∗ f ′ ( N e t n 3 ) = ∑ t = 1 T δ t 4 ∗ W t , n 3 ∗ f ′ ( N e t n 3 ) \begin{aligned} \delta^3_n=-\frac{\partial{Loss}}{\partial{Net^3_n}}\\ &=\sum^{T}_{t=1}(y_t-H^4_t)*f'(Net^4_t)*W^3_{t,n}*f'(Net^3_n)\\ &=\sum^{T}_{t=1}\delta^4_t*W^3_{t,n}*f'(Net^3_n)\tag{17} \end{aligned} δn3=−∂Netn3∂Loss=t=1∑T(yt−Ht4)∗f′(Nett4)∗Wt,n3∗f′(Netn3)=t=1∑Tδt4∗Wt,n3∗f′(Netn3)(17)
(18) δ m 2 = − ∂ L o s s ∂ N e t m 2 = ∑ t = 1 T ( y t − H t 4 ) ∗ f ′ ( N e t t 4 ) ∗ ∑ n = 1 N W t , n 3 ∗ f ′ ( N e t n 3 ) ∗ W n , m 2 ∗ f ′ ( N e t m 2 ) = ∑ t = 1 T δ t 4 ∗ ∑ n = 1 N W t , n 3 ∗ f ′ ( N e t n 3 ) ∗ W n , m 2 ∗ f ′ ( N e t m 2 ) = ∑ n = 1 N ( ∑ t = 1 T δ t 4 ∗ W t , n 3 ∗ f ′ ( N e t n 3 ) ∗ W n , m 2 ∗ f ′ ( N e t m 2 ) ) = ∑ n = 1 N δ n 3 ∗ W n , m 2 ∗ f ′ ( N e t m 2 ) \begin{aligned} \delta^2_m=-\frac{\partial{Loss}}{\partial{Net^2_m}}\\ &=\sum^{T}_{t=1}(y_t-H^4_t)*f'(Net^4_t)*\sum^{N}_{n=1}W^3_{t,n}*f'(Net^3_n)*W^2_{n,m}*f'(Net^2_m)\\ &=\sum^{T}_{t=1}\delta^4_t*\sum^{N}_{n=1}W^3_{t,n}*f'(Net^3_n)*W^2_{n,m}*f'(Net^2_m)\\ &=\sum^{N}_{n=1}(\sum^{T}_{t=1}\delta^4_t*W^3_{t,n}*f'(Net^3_n)*W^2_{n,m}*f'(Net^2_m))\\ &=\sum^{N}_{n=1}\delta^3_n*W^2_{n,m}*f'(Net^2_m)\tag{18} \end{aligned} δm2=−∂Netm2∂Loss=t=1∑T(yt−Ht4)∗f′(Nett4)∗n=1∑NWt,n3∗f′(Netn3)∗Wn,m2∗f′(Netm2)=t=1∑Tδt4∗n=1∑NWt,n3∗f′(Netn3)∗Wn,m2∗f′(Netm2)=n=1∑N(t=1∑Tδt4∗Wt,n3∗f′(Netn3)∗Wn,m2∗f′(Netm2))=n=1∑Nδn3∗Wn,m2∗f′(Netm2)(18)
3.3. 计算 ∂ N e t t 4 ∂ W t , n 3 \frac{\partial{Net^4_t}}{\partial{W^3_{t,n}}} ∂Wt,n3∂Nett4, ∂ N e t n 3 ∂ W n , m 2 \frac{\partial{Net^3_n}}{\partial{W^2_{n,m}}} ∂Wn,m2∂Netn3, ∂ N e t m 2 ∂ W m , i 1 \frac{\partial{Net^2_m}}{\partial{W^1_{m,i}}} ∂Wm,i1∂Netm2:
(19) ∂ N e t t 4 ∂ W t , n 3 = ∂ ∑ n = 1 N ( W t , n 3 ∗ H n 3 ) ∂ W t , n 3 = H n 3 \begin{aligned} \frac{\partial{Net^4_t}}{\partial{W^3_{t,n}}}=\frac{\partial{\sum_{n=1}^N(W_{t,n}^3*H_n^3)}}{\partial{W^3_{t,n}}}=H^3_n\tag{19} \end{aligned} ∂Wt,n3∂Nett4=∂Wt,n3∂∑n=1N(Wt,n3∗Hn3)=Hn3(19)
(20) ∂ N e t n 3 ∂ W n , m 2 = ∂ ∑ m = 1 M ( W n , m 2 ∗ H m 2 ) ∂ W n , m 2 = H m 2 \begin{aligned} \frac{\partial{Net^3_n}}{\partial{W^2_{n,m}}}=\frac{\partial{\sum_{m=1}^M(W_{n,m}^2*H_m^2)}}{\partial{W^2_{n,m}}}=H^2_m\tag{20} \end{aligned} ∂Wn,m2∂Netn3=∂Wn,m2∂∑m=1M(Wn,m2∗Hm2)=Hm2(20)
(21) ∂ N e t m 2 ∂ W m , i 1 = ∂ ∑ i = 1 I ( W m , i 1 ∗ H i 1 ) ∂ W m , i 1 = H i 1 \begin{aligned} \frac{\partial{Net^2_m}}{\partial{W^1_{m,i}}}=\frac{\partial{\sum_{i=1}^I(W_{m,i}^1*H_i^1)}}{\partial{W^1_{m,i}}}=H^1_i\tag{21} \end{aligned} ∂Wm,i1∂Netm2=∂Wm,i1∂∑i=1I(Wm,i1∗Hi1)=Hi1(21)
3.4. 总结
将公式(19-21)带入(13-15),得到
(22) Δ W t , n 3 = η ∗ δ t 4 ∗ ∂ N e t t 4 ∂ W t , n 3 = η ∗ δ t 4 ∗ H n 3 \begin{aligned} \Delta{W^3_{t,n}}=\eta*\delta^4_t*\frac{\partial{Net^4_t}}{\partial{W^3_{t,n}}}=\eta*\delta^4_t*H^3_n\tag{22} \end{aligned} ΔWt,n3=η∗δt4∗∂Wt,n3∂Nett4=η∗δt4∗Hn3(22)
(23) Δ W n , m 2 = η ∗ δ n 3 ∗ ∂ N e t n 3 ∂ W n , m 2 = η ∗ δ n 3 ∗ H m 2 \begin{aligned} \Delta{W^2_{n,m}}=\eta*\delta^3_n*\frac{\partial{Net^3_n}}{\partial{W^2_{n,m}}}=\eta*\delta^3_n*H^2_m\tag{23} \end{aligned} ΔWn,m2=η∗δn3∗∂Wn,m2∂Netn3=η∗δn3∗Hm2(23)
(24) Δ W m , i 1 = η ∗ δ m 2 ∗ ∂ N e t m 2 ∂ W m , i 1 = η ∗ δ m 2 ∗ H i 1 \begin{aligned} \Delta{W^1_{m,i}}=\eta*\delta^2_m*\frac{\partial{Net^2_m}}{\partial{W^1_{m,i}}}=\eta*\delta^2_m*H^1_i\tag{24} \end{aligned} ΔWm,i1=η∗δm2∗∂Wm,i1∂Netm2=η∗δm2∗Hi1(24)
3.5. 权值更新:
(25) W t , n 3 = W t , n 3 + Δ W t , n 3 \begin{aligned} W^3_{t,n}=W^3_{t,n}+\Delta{W^3_{t,n}}\tag{25} \end{aligned} Wt,n3=Wt,n3+ΔWt,n3(25)
(26) W n , m 2 = W n , m 2 + Δ W n , m 2 \begin{aligned} W^2_{n,m} = W^2_{n,m}+\Delta{W^2_{n,m}}\tag{26} \end{aligned} Wn,m2=Wn,m2+ΔWn,m2(26)
(27) W m , i 1 = W m , i 1 + Δ W m , i 1 \begin{aligned} W^1_{m,i}=W^1_{m,i}+\Delta{W^1_{m,i}}\tag{27} \end{aligned} Wm,i1=Wm,i1+ΔWm,i1(27)
偏置
对于偏置项,推倒方法与上述一样。