（一）Matlab工具箱标定单目相机（超详细）

0 前言

1、为什么要进行相机标定？

  在图像测量及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。
  在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定。相机参数的标定是非常关键的环节，其标定结果的精度将直接影响相机工作产生结果的准确性。

2、相机标定常见术语

名称	英文
内参矩阵	Intrinsic Matrix
焦距	Focal Length
主点	Principal Point
径向畸变	Radial Distortion
切向畸变	Tangential Distortion
旋转矩阵	Rotation Matrices
平移向量	Translation Vectors
平均重投影误差	Mean Reprojection Error
重投影误差	Reprojection Errors

1 安装相机标定工具箱

  相机标定的方式方法有很多，matlab标定是其中比较简单的一种。TOOLBOX_calib工具箱和其他工具箱的安装工程一样，将文件夹复制到toolbox下，添加路径即可。TOOLBOX_calib工具箱下载链接：http://www.vision.caltech.edu/bouguetj/calib_doc/

  在这个网站上还有一些相机标定的demo，感兴趣的可以自己复现一下。

2 相机标定

2.1、图像准备

  在相机标定之前，需要进行图像采集。简单讲就是拍摄带有棋盘格的图像，棋盘格网上有很多，自己拿A4纸打印一个即可。我采用的棋盘格规格是7x9,正方形边长10mm。

  采集图像很简单，拿着相机咔咔拍就行了。

2.2、标定（Calibration）

  TOOLBOX_calib工具箱使用起来很简单，在安装目录里面找到toolbox文件夹，然后找到安装的TOOLBOX_calib文件夹。将准备好的图像数据拷贝到改文件夹下，然后开始标定。

  在命令窗口输入calib_gui，会弹出一个Gui窗口。

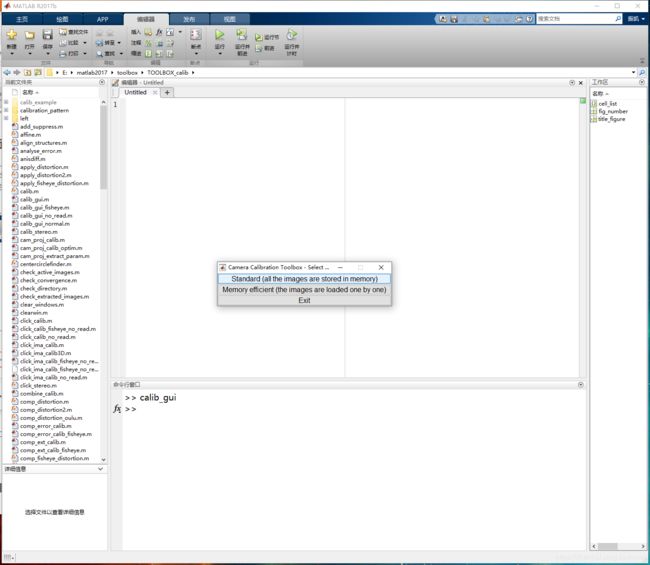
   选择Standard（all the images are stored in memory），进去后界面如下：

   进入存放图片的文件夹，点击Image name，我们可以看到文件夹下的内容。

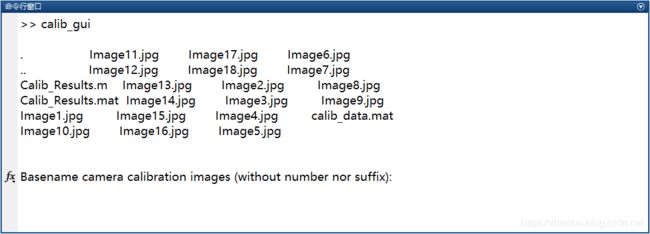
   然后此时提示你输入Basename，Basename就是你的所有图片的名字中相同的部分，例如我将图片统一命名为”Image_“的格式，所以只需在命令行输入Image，然后输入图片格式j。结果如下图所示：

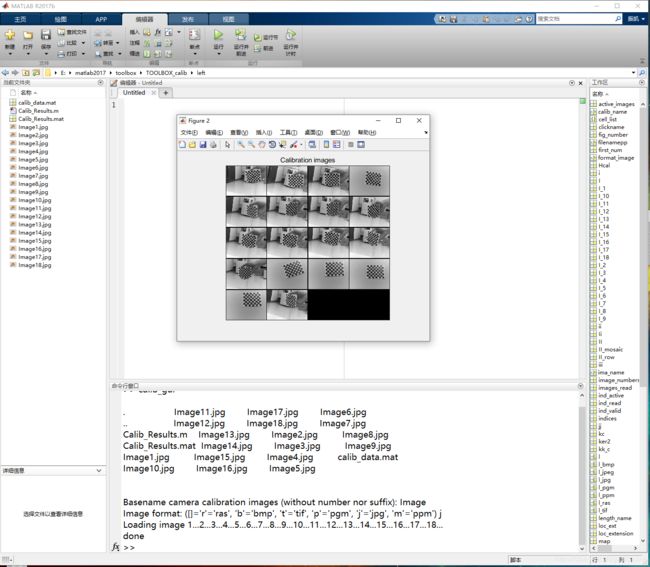
  点击Extract grid corners，提取每幅图的角点。在命令窗口中，直接按回车键（”Enter“）自动计算棋盘格数目。标定时，依次选取棋盘格的四个角点。

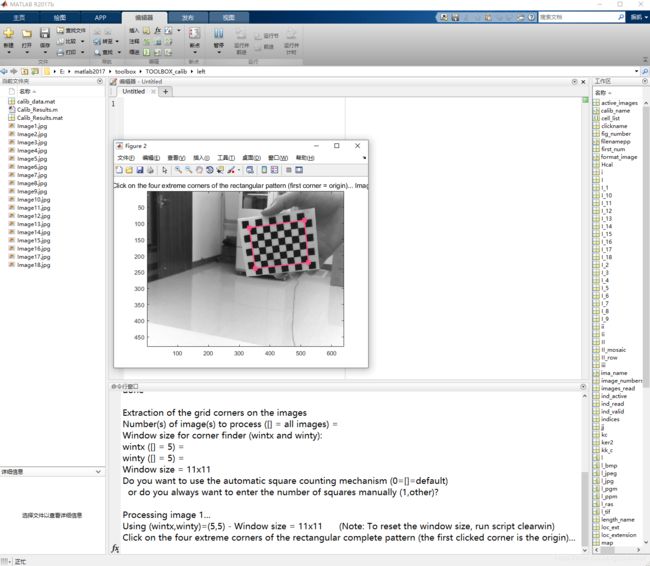
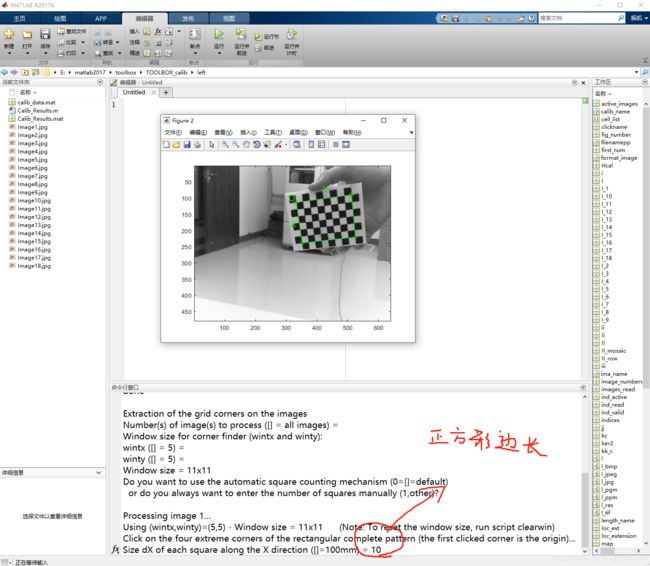
  然后，在命令行里面输入棋盘格正方形边长，即两个角点之间的距离。（我用的棋盘格是1x1cm的，所以设置为10mm）标定结果如下图所示：

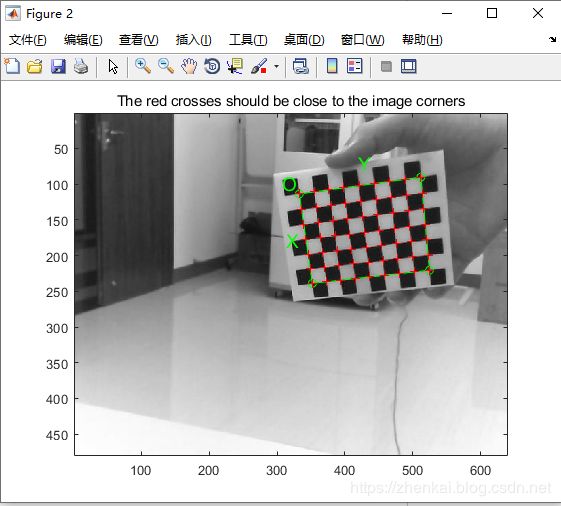
If the guessed grid corners (red crosses on the image) are not close to the actual corners,
it is necessary to enter an initial guess for the radial distortion factor kc (useful for subpixel detection)
Need of an initial guess for distortion? ([]=no, other=yes) 

如果预测的角落接近实际图像角落，则可以跳过以下步骤（如果没有太多的图像失真）。这是当前图像的情况：预测的角落足够接近真实图像角落。因此，没有必要通过输入径向失真系数的猜测来“帮助”软件检测图像角落。按“输入”，使用这些位置作为初始猜测自动提取角。

Corner extraction...

然后自动提取图像角点，并在图3中显示（角点周围的蓝色方块显示角落取景窗口的极限）：

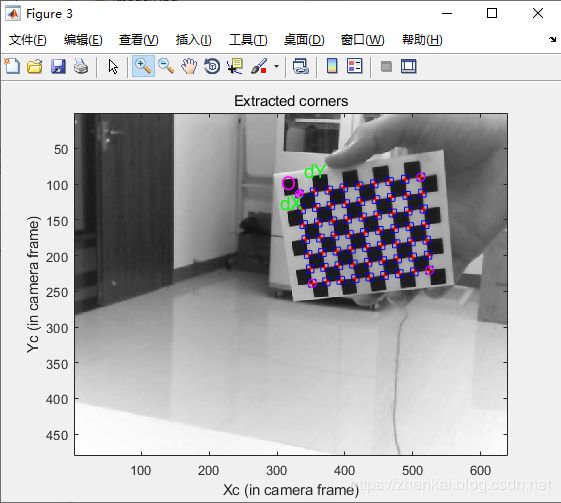
  至此，已经标注完成一张图片，继续重复此步骤完成下面的标定。

2.3、校准

  点击Gui窗口上的Calibration，如图所示：

校准分两步完成：首先进行初始化，然后进行非线性优化。 初始化步骤基于不包括任何镜头失真（程序名称：
init_calib_param.m）计算校准参数的闭合形式解决方案 。 非线性优化步骤使所有校准参数（对于内在的9
DOF：焦点，主点，失真系数和6 * 20 DOF外部=> 129参数）的总重投影误差（在最小二乘意义上）最小化。

Calibration parameters after initialization:

Focal Length:          fc = [ 913.62232   913.62232 ]
Principal point:       cc = [ 319.50000   239.50000 ]
Skew:             alpha_c = [ 0.00000 ]   => angle of pixel = 90.00000 degrees
Distortion:            kc = [ 0.00000   0.00000   0.00000   0.00000   0.00000 ]

Calibration results after optimization (with uncertainties):

Focal Length:          fc = [ 921.52622   916.96292 ] +/- [ 5.81534   5.82907 ]
Principal point:       cc = [ 351.02906   228.92072 ] +/- [ 7.19873   5.76131 ]
Skew:             alpha_c = [ 0.00000 ] +/- [ 0.00000  ]   => angle of pixel axes = 90.00000 +/- 0.00000 degrees
Distortion:            kc = [ 0.05435   -0.29665   0.00090   0.01548  0.00000 ] +/- [ 0.03468   0.50857   0.00299   0.00324  0.00000 ]
Pixel error:          err = [ 0.10736   0.10316 ]

Note: The numerical errors are approximately three times the standard deviations (for reference).

  观察到只需要25次梯度下降迭代才能达到最小值。这意味着只有25次重投影函数+雅可比计算和反演的评估。如图：

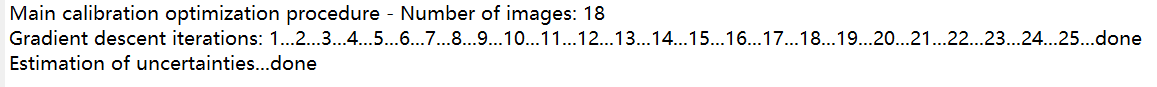
2.4、结果分析

  单击面板上的“Reproject on images”来将网格角点映射到原始图像中。这些映射是基于当前的内参和外参计算出来的。输入一个空字符（直接按"Enter"）作为“Number(s) of image(s) to show([]=all images)”来表示你想查看所有图像，下面的图像显示了最初的四张检测到的角点的图像（叉）以及映射的网格角点（圆）。
  重投影错误以颜色编码十字形的形式显示：

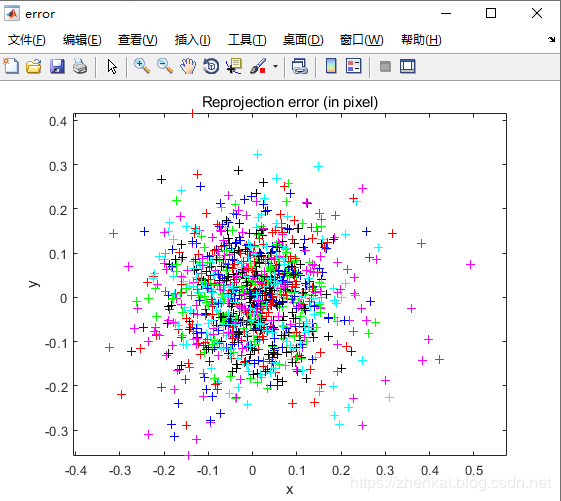
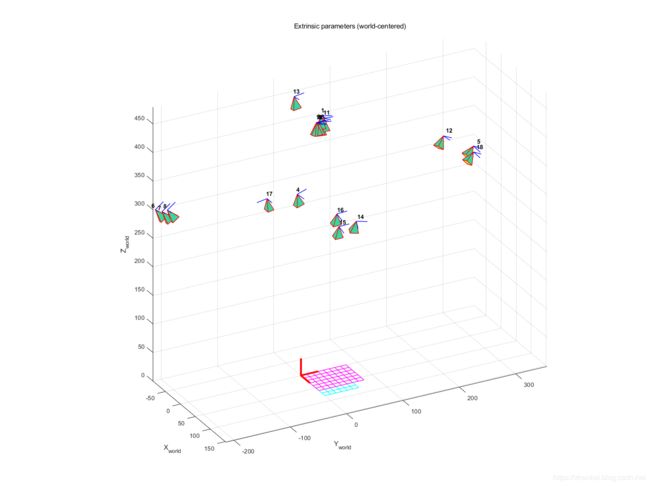
  在面板中单击“ShowExtrinsic”，外参（棋盘格相对于相机的相对位置）就以3D的形式显示出来了：

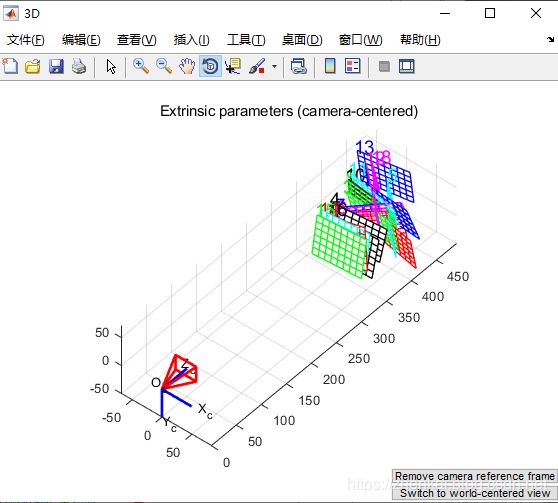
  在该图中，帧 （O c，X c，Y c，Z c）是相机参考帧。红色金字塔对应于由图像平面定义的相机的有效视野。要从“以摄像机为中心”视图切换到“以世界为中心”视图，只需单击位于图左下角的切换到以世界为中心的视图按钮即可。

  单击“Save”保存标定结果（内参和外参）到matlab文件“Calib_Results.mat”

3 小结

  以上就是利用matlab工具箱标定相机的主要步骤，后面会介绍一下双目相机的标定和相机标定参数的应用，利用双目相机拍摄的图片上的任意一点求取其空间坐标。需要相机标定板或者其他资料的可以给我留言，有时不能及时回复消息，见谅！