正在学习的比较详细的机器学习教程（不断更新）

使用MINIST数据集
https://blog.csdn.net/zhaohaibo_/article/d

// 获取 minist 数据集
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("E:/python/data/minist", one_hot=True)   

机器学习实战（一）——机器学习主要任务

https://blog.csdn.net/jiaoyangwm/article/details/79478066

• 分类是机器学习的一项主要任务，主要是将实例数据划分到合适的分类中。
• 机器学习的另外一项任务是回归，主要是预测数值型的数据，比如通过数据值拟合曲线等。

分类和回归属于监督学习：
通过已有的训练样本（即已知数据及其对应的输出）去训练得到一个最优模型（这个模型属于某个函数的集合，最优表示某个评价准则下是最佳的），再利用这个模型将所有的输入映射为相应的输出，对输出进行简单的判断从而实现分类的目的。也就具有了对未知数据分类的能力。监督学习的目标往往是让计算机去学习我们已经创建好的分类系统（模型）。

与监督学习相对应的是无监督学习：
输入数据没有被标记，也没有确定的结果。样本数据类别未知，需要根据样本间的相似性对样本集进行分类（聚类，clustering）试图使类内差距最小化，类间差距最大化。此时数据没有类别信息，也不会给定目标值。寻找描述数据统计值的过程称之为密度估计。此外，无监督学习可以减少数据特征的维度，以便我们可以使用二维或三维图形更加直观的展示数据信息。

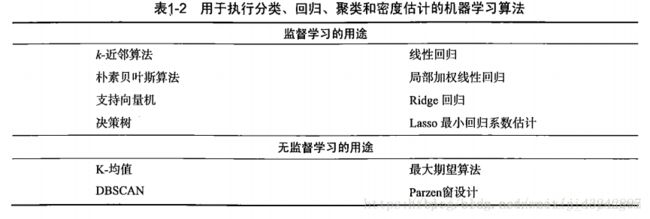
表1-2列出了机器学习的主要任务，以及解决相应问题的算法。

机器学习实战（二）——k-近邻算法

https://blog.csdn.net/jiaoyangwm/article/details/79480275

k近邻法(k-nearest neighbor, k-NN)是1967年由Cover T和Hart P提出的一种基本分类与回归方法。它的工作原理是：存在一个样本数据集合，也称作为训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后，将新的数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本最相似数据(最近邻)的分类标签。一般来说，我们只选择样本数据集中前k个最相似的数据，这就是k-近邻算法中k的出处，通常k是不大于20的整数。最后，选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

k-近邻算法没有进行数据的训练，直接使用未知的数据与已知的数据进行比较，得到结果。因此，可以说k-邻近算法不具有显式的学习过程。

距离度量：


归一化数值处理：

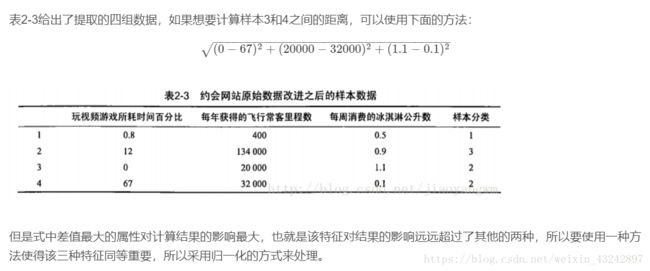
我的理解是：已知若干个一维矩阵向量及其所属分类，给定一未知分类的矩阵向量，计算距离并按照从小到大的顺序排列，取前k个分类结果，统计出现次数最多的结果，即为最终分类结果。
例如：做手写字体识别，先将二进制图像矩阵转化为一维向量，进行计算（python中可以直接调相应的库函数完成距离计算并进行统计）

机器学习实战（四）——基于概率论的分类方法：朴素贝叶斯

https://blog.csdn.net/jiaoyangwm/article/details/79552267
朴素贝叶斯(naive Bayes)算法是有监督的学习算法，解决的是分类问题，如客户是否流失、是否值得投资、信用等级评定等多分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。但由于该算法以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提，就会导致算法精度在某种程度上受影响。
在统计资料的基础上，依据某些特征，计算各个类别的概率，从而实现分类。
“朴素”的解释：
假设各个特征之间相互独立（在贝叶斯分类器上做了简化）
朴素贝叶斯的基础假设：

①每个特征相互独立；
②每个特征的权重（或重要性）都相等，即对结果的影响程度都相同。

朴素贝叶斯具体实现步骤：

机器学习实战（五）——Logistic 回归

https://blog.csdn.net/jiaoyangwm/article/details/79570864
https://blog.csdn.net/xlinsist/article/details/51236454
https://blog.csdn.net/xlinsist/article/details/51264829

机器学习实战（六）——支持向量机

https://blog.csdn.net/jiaoyangwm/article/details/79579784

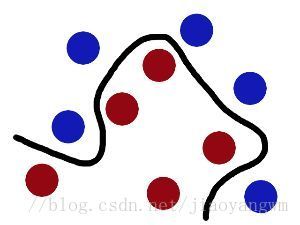
这些球叫做 「data」，把棍子 叫做 「classifier」分类器, 最大间隙trick 叫做「optimization」最优化， 拍桌子叫做「kernelling」, 那张纸叫做「hyperplane」超平面。
当数据为线性可分的时候，也就是可以用一根棍子将两种小球分开的时候，只要将棍子放在让小球距离棍子的距离最大化的位置即可，寻找该最大间隔的过程就叫做最优化。

但是一般的数据是线性不可分的，所以要将其转化到高维空间去，用一张纸将其进行分类，空间转化就是需要核函数，用于切分小球的纸就是超平面。
达到在统计样本量较少的情况下，亦能获得良好统计规律的目的。

SVM
通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。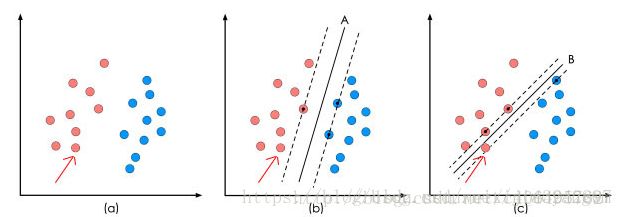
在保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位置就会产生错分现象），如虚线所示。
虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。
两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。显然每一个可能把数据集正确分开的方向都有一个最优决策面（有些方向无论如何移动决策面的位置也不可能将两类样本完全分开），而不同方向的最优决策面的分类间隔通常是不同的，那个具有“最大间隔”的决策面就是SVM要寻找的最优解。
而这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为”支持向量”。
学习的目标是在特征空间中找到一个分离超平面，能将实例分到不同的类中。
分离超平面的方程：w⋅x+b=0
方程由法向量w和截距b决定，可以用(w,b)来表示。

分离超平面将特征空间划分为两部分，一部分为正类，一部分为负类，法向量指向的一侧为正类，另一侧为负类。
二次规划： https://blog.csdn.net/lilong117194/article/details/78204994
SVM（1）：理清分离超平面方程和法向量 https://blog.csdn.net/Jiajing_Guo/article/details/65628378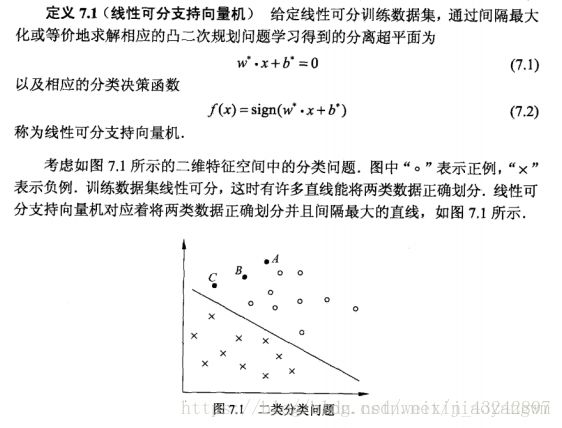

机器学习系列(14)_SVM碎碎念part2：SVM中的向量与空间距离
https://blog.csdn.net/han_xiaoyang/article/details/52679559

信息熵到底是什么

https://blog.csdn.net/saltriver/article/details/53056816

一、线性回归和逻辑回归

https://blog.csdn.net/jiaoyangwm/article/details/81139362

二、SVM

https://blog.csdn.net/jiaoyangwm/article/details/81117958

机器学习实战（九）树回归

https://blog.csdn.net/jiaoyangwm/article/details/79631480

分类与回归区别？
logistic回归不是回归是分类

机器学习实战（三）——决策树

https://blog.csdn.net/jiaoyangwm/article/details/79525237#312-编写代码计算经验熵

[Machine Learning & Algorithm] 随机森林（Random Forest）

http://www.cnblogs.com/maybe2030/p/4585705.html#_label6

TensorFlow入门深度学习–01.基础知识

https://blog.csdn.net/drilistbox/article/details/79721099#111-安装gpu版本。