伏格尔法、位势法寻找闭回路

汇报题目：

如何通过伏格尔法找到初始运输方案、并寻找矩阵里的闭回路？

背景：

在线性规划里，我们解决运输问题时可以使用表上作业法；表上作业法的基本步骤是确定初始运输方案、判断是否为最优运输方案、非最优运输方案时调整运输方案；其中，确定初始运输方案时可以用最小元素法、西北角法、伏格尔法等；而在调整运输方案时，我们需要找到一个闭回路；今天，我就和大家一起学习一下如何用Matlab通过伏格尔法求得初始运输方案，以及在进行运输方案的调整时如何找到那个闭回路。

方法与原理

伏格尔法：
在讨论伏格尔法之前，我们先看一下最小元素法；最小元素法就是在每次确定运量的时候都最优考虑运价中最小的，这在一定程度上可以得到一个满意的结果，但是可能出现一种情况，就是当我们节省了某一处的费用的时候，可能在另一处就会花费数倍的费用，得不偿失。

鉴于此，伏格尔法考虑到，当某地的产品不能以最小运价就近供应时，就考虑次小运费；最小运费与次小运费之间就有一个差额，差额越大，就说明当不能按最小运费运输时，运费增加越多；所以伏格尔法每次会选择差额最大处，并采用此处的最小运费运输。

寻找闭回路：

从每一空格出发一定存在和可以找到唯一的闭回路。因为（m+n-1)个数字格对应的系数向量是一个基。

下面给出一个伏格尔法计算的实例：

下面给出一个求回路的例子：

实现过程：
首先我们看一下如何求行差额与列差额：

function B = Difference(A)
%设矩阵时m行n列的，返回的矩阵B位1行m+n列的矩阵，记录多的是矩阵的行差额与列差额。

计算行差额：

%计算最下值
for  i=1:m
    temp1 = inf;
    temp2 = inf;
    for j=1:n
      if temp1>A(i,j)&&A(i,j)~=-inf    %这里的-inf与之前对划掉的行或列的赋值有关
          temp1 = A(i,j);
          v = i;h = j;
      end
    end

%计算次小值
 flage = 0;
    for j=1:n
     %    h;
         
        if temp2>A(i,j)&&((j~=h))&&A(i,j)~=-inf
            temp2 = A(i,j);
            flage = 1;%标识存在次小元素，即至少有两个元素
        end

求行差额

 if flage==1   %判断该行是否存在两个或两个未被使用的量
    B(i)=temp2-temp1;
     else B(i)=-inf;
        end

同理求列差额：

for i=1:n
    temp1 = inf;
    temp2 =inf;
    for j=1:m
      if temp1>A(j,i)&&A(j,i)~=-inf
          temp1 = A(j,i);
          u = j;
          d = i;
      end
    end
    flage =0;
    for j = 1:m
    if temp2>A(j,i)&&(j~=u)&&A(j,i)~=-inf
        temp2 = A(j,i);
        flage = 1;
    end
    end
    if flage ==1
    B(m+i)=temp2-temp1;
    else B(m+i)=-inf;
    end
end
end
end

通过求差额，我们可以得到一个矩阵的差额向量

下面就开始用伏格尔法确定初始运输方案了：

function B = Vogel1(A,X)
%其中矩阵B是给出的初始运输方案，如果有运量，则为具体数值，否则为0

首先找到最大差额处：

C = Difference(A);
[m,n]=size(A);
temp1 = -inf;
H=ones(1,m+n);%H判断该行或该列是否被划掉，先行后列的一维数组

for i =1:m+n
    if temp1 

这样v就记录了最大差额处的下标

下面将v分为两种情况来讨论，即当最大差额为行差额或列差额时：

if v<=m
    [mm,index]=min1(A(v,:));  %找到该行的最小运价
    B(v,index)=min(X(v),X(m+index));  %在最小运价处应填入的数字
    X(v) = X(v)-B(v,index); %对产量进行更新
    X(m+index)=X(m+index)-B(v,index);  %对销量进行更新

接下来我们应该看是否可以划掉某一行或某一列：

 %判断是否划掉行或列
    if (X(v)==0)    %划掉一行
       H(v)=0; 
       A(v,:)=[-inf];%赋值为负无穷大而不是将其删掉
    end
    if(X(m+index)==0)
        H(m+index) = 0;
        A(:,index)=[-inf];
    end
end

注意：当我们要划掉一行或是一列的时候并不是真正的把它删掉，而是将整行或整列都赋为负无穷；因为如果删掉的话会导致矩阵的维数改变

同理当最大差额为列差额时：

if v>m

    
   [mm,index]=min1(A(:,v-m)');   %注：这里应该将矩阵转置
    B(index,v-m)=min(X(index),X(v));
    X(index) = X(index)-B(index,v-m);
    X(v) = X(v)-B(index,v-m);
    %判断是否划掉行或列
   if X(index)==0
       H(index)=0;
       A(index,:)=[-inf];
   end
       if X(v)==0
           H(v)=0;
           A(:,v-m)=[-inf];
           
       end
end

这里还有一个问题就是当一行或一列剩下最后一个元素时，根据表上作业法是需要我们再添加一个运量的，这里我们又如何完成呢？

首先我们得在求差额的时候设置当只有一个元素时差额为-inf

之后我们再定义一个函数finding,用以找到矩阵中非负无穷元素，并返回下标

function [x,y]=finding(A)
[m,n] = size(A);
for i = 1:m
    for j = 1:n
        if A(i,j)~=-inf
            x = i;
            y=j;
            break
     end
    end
end

if Difference(A)==-inf    %当我们的矩阵同行或同列只有一个元素时
    [x,y]=finding(A);
    B(x,y) = min(X(x),X(m+y));
    H = zeros(m+n);   %H赋0是整个while循环的终止条件
end

注：上述操作为产销平衡条件下，因为产销不平衡时未必可以将差额矩阵化为全为-inf的情形；而产销不平衡问题我们是可以转化为产销平衡问题的

这样，通过伏格尔法确定初始运输方案就写完了

最后给大家讲一下如何找到矩阵里的闭回路：
比如说这个矩阵：

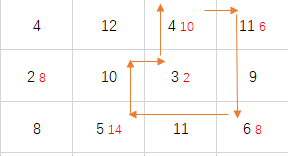
我们首先来分析一下，但我们从某一个空格出发时，在该空格处有4个方向可走，当我们走第二个格子的时候，当这个格子为空格时，只有一种方向；当这个格子为数字格时，有三种方向可走；依次循环下去，直到与始点重合。这里我们应该注意的是，当我们确定当下这个格子往哪走的时候，需要直知道前一个格子的位置，因为在数字格处我们只能直走，例如当当前一个点为（i,j)而前一个点为（i-1,j)时，下一个点为（i+1,j);这对于矩阵里很多个点来说，无疑是复杂的，这里我在写这个方法的初期页尝试过，写的点的行走函数如下：

%在知道现在点所在位置与前一个点所在位置的情况下，确定下一个点所在位置
function [x,y,p] = run(i,j,W,I,J)
[m,n] = size(W);
x(1) = i;
y(1) = j;
p = 1;
flage = 0 ;
flage1 = 0;
k=1;
if W(i,j)~=-inf
    if i>I&&i+1<=m
        x(1) = i+1;
   flage1 = 1;
        %else 
     %  flage = 1;
    end
    if i=1
        x(1) = i-1;
    flage1 = 1;
        %else
     %   flage =1;
    end
    if j>J&&j+1<=n
        y(1) = j+1;
    flage1 = 1;
        %else
     %   flage = 1;
    end
    if j=1
        y(1) = j-1;
    flage1 = 1;
        %else
     %   flage = 1;
    end
    if flage ==1
         p =0; 
    end
else
     if i>I
        if i+1<=m
            x(k) = i+1;
            y(k) = j;
            k = k+1;
            flage1 =1; 
        end
        if j+1<=n
        x(k) = i;
        y(k) = j+1;
        k = k+1;
        flage1 = 1;
        end
        if j-1>=1
            x(k) = i;
            y(k) = j-1;
            k = k+1;
            flage1 = 1;
        end
    end
     if i1
            x(k) = i-1;
            y(k) = j;
            k = k+1;
            flage1 = 1;
        end
        if j+1<=n
        x(k) = i;
        y(k) = j+1;
        k = k+1;
        flage1 = 1;
        end
        if j-1>=1
            x(k) = i;
            y(k) = j-1;
            k = k+1;
            flage1 = 1;
        end
    end
    if j>J
        if j+1<=n
            x(k) = i;
            y(k) = j+1;
            k = k+1;
            flage1 = 1;
        end
        if i+1<=m
            x(k) =i+1;
            y(k) = j;
            k = k+1;
            flage1 = 1;
        end
        if i-1>=1
            x(k)=i-1;
            y(k) = j;
            k = k+1;
            flage1 = 1;
        end
    end
     if j=1
            x(k) = i;
            y(k) = j-1;
            k = k+1;
            flage1 = 1;
        end
        if i+1<=m
            x(k) =i+1;
            y(k) = j;
            k = k+1;
            flage1 = 1;
        end
        if i-1>=1
            x(k)=i-1;
            y(k) = j;
            k = k+1;
            flage1 = 1;
        end
     end
end
       if flage1 ==1
           p=1;
       end

这个函数可以通过前一个点与当前点得到下一个点的所有可能，并将其储存在矩阵里

然而，有没有更好的方法来确定这一回路呢，我们再来观察一下这个矩阵：

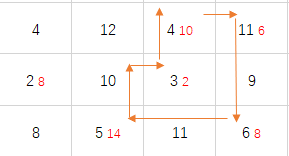
其中有一个规律：从某一个空格开始，它的回路有这样一个特征，即存在某一个矩形，该矩形的边上有初始空格，并且三个顶点上均为数字格（该矩形的某些边也可以隐性表达）这个规律我是通过对一个矩阵进行行遍历与列遍历来发挥它的做用的

所谓行遍历，就是遍历某一行，找到其中为-inf的格子；列遍历就是在一列中找到为-inf的格子 （这里我设置的数字格为-inf)

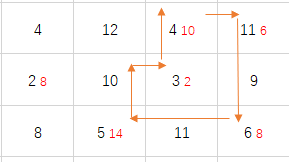
我们先大致介绍一下这个方法：
以10为例，先行遍历，找到为-inf的格子W（2，1）和W（2，3），之后列遍历，找到为-inf的格子W(1，3）；之后再从W（1，3）处行遍历，找到为-inf的格子W（1，4）；再从W（1，4）处列遍历，找到为-inf 的格子W（3，4）；再从W（3，4）处行遍历，找到为-inf的格子W(3,2);因为格子W（3，2）与初始格子W（2，2）有相同的列数，所以跳出循环，找到回路。

总结

对与今天所讲的内容，主要的难点在于采用何种方式去实现一个算法，有时候我们自然想到的很朴素的做法可能很难实现，需要我们揣摩其中的规律