智乃与无意义的题目（西工大校赛 线段树）

哇！一看就是智乃姐姐出的题

题目链接
2020年西北工业大学“编程之星”程序设计挑战赛（大学生程序设计创新实践基地队员春季选拔赛）

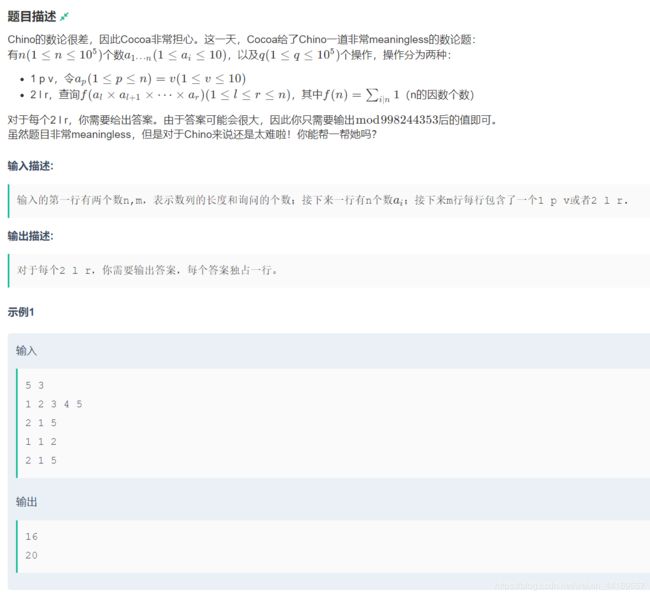
分析：
看到修改和查询想到的就是线段树，但是要用线段树维护什么东西还得继续分析。$f(n)={\sum }_{i|n}1$ 是 $n$ 的因子个数，求一个数的因子个数我们可以想到与唯一分解定理有关的一个公式：
$$n=p_1^{e_1}\times p_2^{e_2}\times p_3^{e_3}\times ...\times p_k^{e_k}$$ 那么 $n$ 的因子个数 $$f(n)=(e_1+1)\times (e_2+1)\times (e_3+1)\times ...\times (e_k+1)$$ 然后我们观察区间查询操作 $f(a_l\times a_{l+1}\times ...\times a_r)(1\le l\le r<n)$ ，对于 ${\prod }_{i=l}^r{a}_i$ 其实就是 $e_i$ 相加，而且 $1\le a_i\le 10$ ，10 以内的质数只有 2,3,5,7 ，所以我们只需要维护这4个数的指数的和。

Code：

#include 
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const int N = 1e5 + 5;
int n, m, a[N];
struct node
{
    int pc[5]; //2,3,5,7
} tree[N << 2];
int p[5] = {0, 2, 3, 5, 7};
int tl(int root) { return root << 1; }
int tr(int root) { return root << 1 | 1; }
void pushup(int root)
{
    int l = tl(root), r = tr(root);
    for (int i = 1; i <= 4; i++)
    {
        tree[root].pc[i] = tree[l].pc[i] + tree[r].pc[i];
    }
}
void buildtree(int l, int r, int root)
{
    if (l == r)
    {
        int t = a[l];
        for (int j = 1; j <= 4; j++)
        {
            tree[root].pc[j] = 0;
            while (t % p[j] == 0)
            {
                tree[root].pc[j]++;
                t /= p[j];
            }
        }
        return;
    }
    int mid = (l + r) >> 1;
    buildtree(l, mid, tl(root));
    buildtree(mid + 1, r, tr(root));
    pushup(root);
}
void update(int pos, int val, int l, int r, int root)
{
    if (l == pos && r == pos)
    {
        int t = val;
        for (int j = 1; j <= 4; j++)
        {
            tree[root].pc[j] = 0;
            while (t % p[j] == 0)
            {
                tree[root].pc[j]++;
                t /= p[j];
            }
        }
        return;
    }
    int mid = (l + r) >> 1;
    if (mid >= pos)
        update(pos, val, l, mid, tl(root));
    else
        update(pos, val, mid + 1, r, tr(root));
    pushup(root);
}
int query(int L, int R, int l, int r, int root, int i)
{
    if (L <= l && r <= R)
    {
        return tree[root].pc[i];
    }
    int mid = (l + r) >> 1;
    int ans = 0;
    if (L <= mid)
        ans += query(L, R, l, mid, tl(root), i);
    if (mid < R)
        ans += query(L, R, mid + 1, r, tr(root), i);
    return ans;
}
int main()
{
#ifdef LOCAL_LIUZHIHAN
    freopen("in.in", "r", stdin);
    // freopen("out.out", "w", stdout);
#endif
    ios::sync_with_stdio(false), cin.tie(nullptr);
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    buildtree(1, n, 1);
    while (m--)
    {
        int k, x, y;
        cin >> k >> x >> y;
        if (k == 1)
        {
            update(x, y, 1, n, 1);
        }
        else if (k == 2)
        {
            ll res = 1;
            for (int i = 1; i <= 4; i++)
            {
                res = (res % mod * (query(x, y, 1, n, 1, i) + 1) % mod) % mod;
            }
            cout << res << endl;
        }
    }
    return 0;
}