深度学习必会模型：VGG模型原理及PyTorch代码

---

1、为什么要引入卷积神经网络？

1.1 三个观察

• 一些特征占据的像素点远小于整张图片的像素点，某个神经元判断一张图片中有没有某一特征不需要看整张图片，所以每个神经元只用连接到一个小块的区域而不需要连接到一张完整的图（卷积层的作用）；
  
• 同样的特征有可能出现在图片的不同区域，但是它们代表同样的含义也有着同样的形状，所以可以用同样的神经元同样的参数就可以侦测出来，可以减少参数的数量（卷积层的作用）；
  
• 对图片的subsampling操作对于图像识别来说并不会有很大的影响，我们可以用这个概念把图片变小这样就可以减小参数（池化层的作用）；
  

1.2 卷积层和池化层

1.2.1 卷积层

• 每一个kernel是一个矩阵，矩阵中的每个参数就是卷积神经网络需要学习的参数，现在图中每一个kernel是 $3\times 3$ 的大小，就意味着在一个 $3\times 3$ 的小区域内寻找某一种特征（对应第一个观察）；
  
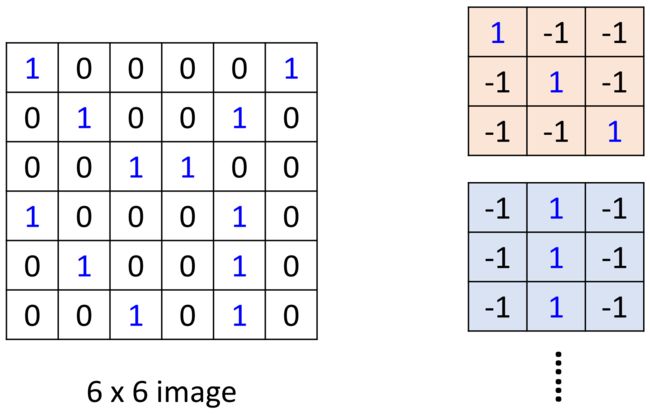
• 将每个kernel按照设定好的stride移动，就可以将一个 $6\times 6$ 的图片变成一个 $4\times 4$ 的图片。这个kernel的作用就是侦查这个图片里面有没有从左上到右下连续的1出现，然后他就会告诉我们要侦测的特征出现在这个图的左上和左下，所以左上和左下就出现了最大值（对应第二个观察）；
  
• 用多个kernel进行互相关运算之后得到的就叫做特征图，很容易得出特征图的通道数其实就是卷积核的个数，例如如果此处有100个卷积核，那么特征图的通道数就会变成100，所以通道的变化就由1变成了100，通道的变化是由于卷积核的数目造成的。
  
• 如果是彩色的图片，每一个像素其实是由三个通道组成（RGB），那么对应的卷积核就要变成一个长方体，卷积核的通道数要和输入的通道数匹配。卷积核的通道数由输入的通道数决定，特征图的通道数由卷积核的个数决定；
  
• 卷积层网络和全连接网络的关系：

还是用MLP的思想将图像展开成一个很长的向量，将互相关运算出的像素值当做这一层的一个输出值，那么就会发现和3这个输出值相连的并不是所有的输入值，而只是和我这个卷积核对应大小的一部分，这样就可以做到减小参数；

当卷积核移动后同样的操作，这一次的输出也只是跟下一个框框里的输入有关，而且这一次的权重和上一次的权重是一样的，因为他们用的同一个卷积核，所以这样就又做了一次参数的减少；

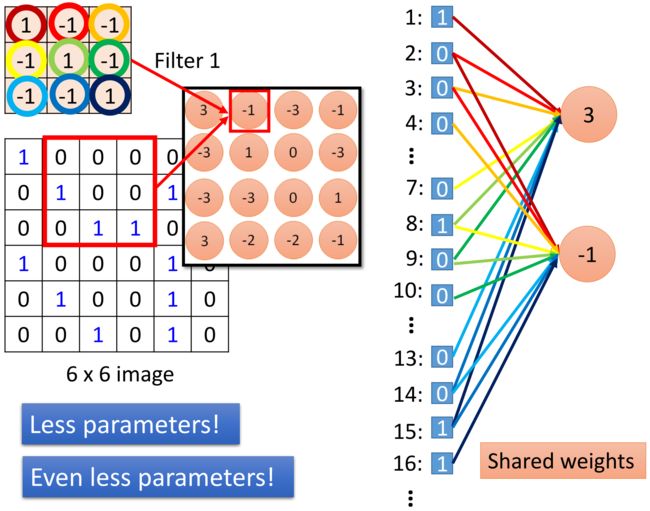
1.2.2 池化层

• 池化层相比于卷积层更简单，就是将卷积后的图片进行subsampling，分组后进行平均或者最大化处理，可以将图片进行缩小（第三个观察）；
  

---

2、VGG模型原理

2.1 提出VGG的动机

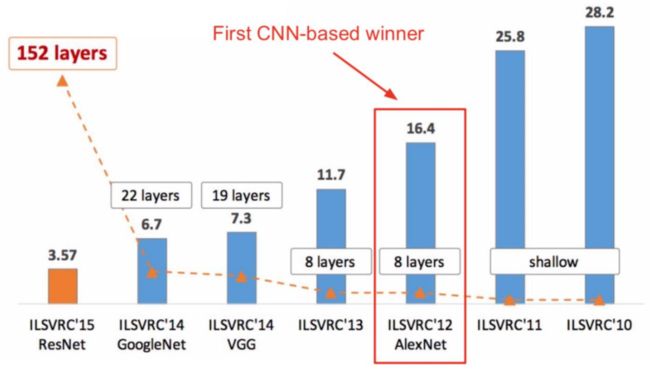
AlexNet是由Alex Krizhevsky提出的首个应用于图像分类的深层卷积神经网络，该网络在2012年ILSVRC (ImageNet Large Scale Visual Recognition Competition)图像分类竞赛中以16.4%的测试错误率赢得第一名。AlexNet使用GPU代替CPU进行运算，使得在可接受的时间范围内模型结构能够更加复杂，它的出现证明了深层卷积神经网络在复杂模型下的有效性，使CNN在计算机视觉中流行开来，直接或间接地引发了深度学习的热潮。Reference: ImageNet Classifification with Deep Convolutional Neural Networks

AlexNet一共包含8层，前5层由卷积层组成，而剩下的3层为全连接层。网络结构分为上下两层，分别对应两个GPU的操作过程。最后一层全连接层的输出作为$softmax$的输入，得到1000个图像分类标签对应的概率值。除去GPU并行结构的设计，AlexNet网络结构与LeNet十分相似。

后来就有人想AlexNet之所以比LeNet效果好有一部分原因是因为网络变深了，但是现在AlexNet里面的部分卷积核尺寸太大了，这样妨碍了网络变深，那么如何改进呢？首先要引入感受野的概念

感受野（Receptive Field），指的是神经网络中神经元“看到的”输入区域，在卷积神经网络中，feature map上某个元素的计算受输入图像上某个区域的影响，这个区域即该元素的感受野。那么如果在我感受野相同的条件下，我让中间层数更多，那么能提取到的特征就越丰富，效果就会更好。

从图中可以看出对于一个 $5\times 5$ 的图片，用两个 $3\times 3$ 的卷积核和用一个 $5\times 5$ 的卷积核最后得到的元素感受野是一样的，但是前者将神经网络加深了一层，并且参数量也少了， $11\times 11$ 的卷积核亦是如此，所以由这种思想便引入了后面的VGG块以及VGG网络。

2.2 VGG模型及其参数的数量

VGGNet是由牛津大学视觉几何小组（Visual Geometry Group, VGG）提出的一种深层卷积网络结构，网络名称VGGNet取自该小组名缩写。VGGNet是首批把图像分类的错误率降低到10%以内模型，同时该网络所采用的$3\times 3$卷积核的思想是后来许多模型的基础，该模型发表在2015年国际学习表征会议（International Conference On Learning Representations, ICLR）后至今被引用的次数已经超过1万4千余次。

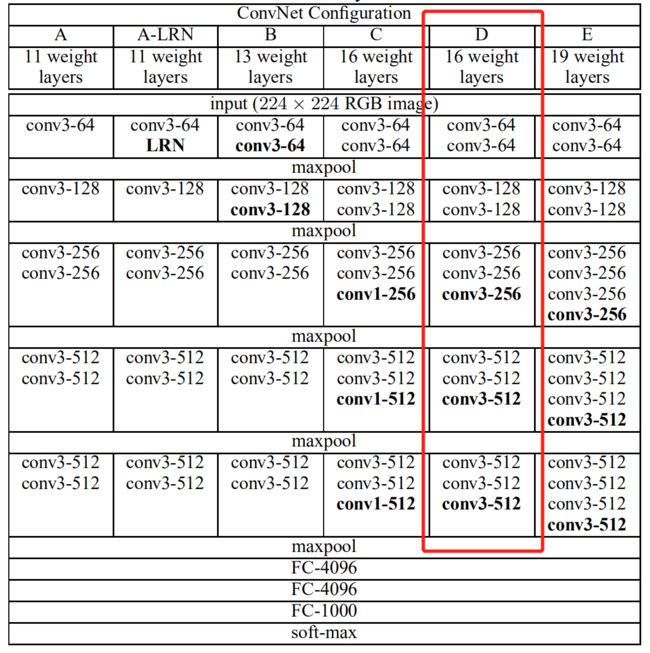
在原论文中的VGGNet包含了6个版本的演进，分别对应VGG11、VGG11-LRN、VGG13、VGG16-1、VGG16-3和VGG19，不同的后缀数值表示不同的网络层数（VGG11-LRN表示在第一层中采用了LRN的VGG11，VGG16-1表示后三组卷积块中最后一层卷积采用卷积核尺寸为 $1\times 1$ ，相应的VGG16-3表示卷积核尺寸为 $3\times 3$ ）。今天主要介绍的VGG16为VGG16-3。

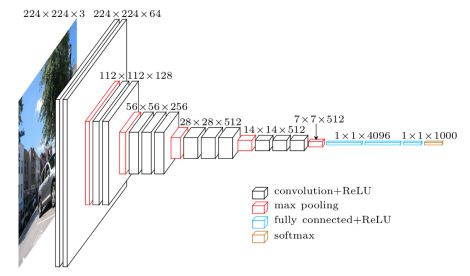
上图中的VGG16体现了VGGNet的核心思路，使用 $3\times 3$ 的卷积组合代替大尺寸的卷积（2个 $3\times 3$ 卷积即可与 $5\times 5$ 卷积拥有相同的感受视野）。

VGG块的组成规律是：连续使用数个相同的填充为1、窗口形状为 $3\times 3$ 的卷积层后接上一个步幅为2、窗口形状为 $2\times 2$ 的最大池化层。卷积层保持输入的高和宽不变，而池化层则对其减半。

网络参数设置如下表所示。

网络层	输入尺寸	核尺寸	输出尺寸	参数个数
卷积层$C_{11}$	$224\times 224\times 3$	$3\times 3\times 64/1$	$224\times 224\times 64$	$(3\times 3\times 3+1)\times 64$
卷积层$C_{12}$	$224\times 224\times 64$	$3\times 3\times 64/1$	$224\times 224\times 64$	$(3\times 3\times 64+1)\times 64$
最大池化层$S_{max1}$	$224\times 224\times 64$	$2\times 2/2$	$112\times 112\times 64$	$0$
卷积层$C_{21}$	$112\times 112\times 64$	$3\times 3\times 128/1$	$112\times 112\times 128$	$(3\times 3\times 64+1)\times 128$
卷积层$C_{22}$	$112\times 112\times 128$	$3\times 3\times 128/1$	$112\times 112\times 128$	$(3\times 3\times 128+1)\times 128$
最大池化层$S_{max2}$	$112\times 112\times 128$	$2\times 2/2$	$56\times 56\times 128$	$0$
卷积层$C_{31}$	$56\times 56\times 128$	$3\times 3\times 256/1$	$56\times 56\times 256$	$(3\times 3\times 128+1)\times 256$
卷积层$C_{32}$	$56\times 56\times 256$	$3\times 3\times 256/1$	$56\times 56\times 256$	$(3\times 3\times 256+1)\times 256$
卷积层$C_{33}$	$56\times 56\times 256$	$3\times 3\times 256/1$	$56\times 56\times 256$	$(3\times 3\times 256+1)\times 256$
最大池化层$S_{max3}$	$56\times 56\times 256$	$2\times 2/2$	$28\times 28\times 256$	$0$
卷积层$C_{41}$	$28\times 28\times 256$	$3\times 3\times 512/1$	$28\times 28\times 512$	$(3\times 3\times 256+1)\times 512$
卷积层$C_{42}$	$28\times 28\times 512$	$3\times 3\times 512/1$	$28\times 28\times 512$	$(3\times 3\times 512+1)\times 512$
卷积层$C_{43}$	$28\times 28\times 512$	$3\times 3\times 512/1$	$28\times 28\times 512$	$(3\times 3\times 512+1)\times 512$
最大池化层$S_{max4}$	$28\times 28\times 512$	$2\times 2/2$	$14\times 14\times 512$	$0$
卷积层$C_{51}$	$14\times 14\times 512$	$3\times 3\times 512/1$	$14\times 14\times 512$	$(3\times 3\times 512+1)\times 512$
卷积层$C_{52}$	$14\times 14\times 512$	$3\times 3\times 512/1$	$14\times 14\times 512$	$(3\times 3\times 512+1)\times 512$
卷积层$C_{53}$	$14\times 14\times 512$	$3\times 3\times 512/1$	$14\times 14\times 512$	$(3\times 3\times 512+1)\times 512$
最大池化层$S_{max5}$	$14\times 14\times 512$	$2\times 2/2$	$7\times 7\times 512$	$0$
全连接层$F{C}_1$	$7\times 7\times 512$	$(7\times 7\times 512)\times 4096$	$1\times 4096$	$(7\times 7\times 512+1)\times 4096$
全连接层$F{C}_2$	$1\times 4096$	$4096\times 4096$	$1\times 4096$	$(4096+1)\times 4096$
全连接层$F{C}_3$	$1\times 4096$	$4096\times 1000$	$1\times 1000$	$(4096+1)\times 1000$

---

3、核心代码

import torch
import torch.nn as nn

# 将一个卷积层、BN层和非线性层封装在一起
def conv_layer(channel_in, channel_out, kernel_size, padding_size):
  
    layer = nn.Sequential(
      nn.Conv2d(channel_in,channel_out,kernel_size=kernel_size,padding=padding_size),
      nn.BatchNorm2d(channel_out),
      nn.ReLU()
    )
    
    return layer

# 将上述封装的卷积层按照指定的参数组装在一起，最后再加一个最大池化层
def vgg_conv_block(channel_in_list, channel_out_list, kernel_size_list,                                  padding_size_list, pooling_kernel_size, pooling_stride):

    layers = [conv_layer(channel_in_list[i], channel_out_list[i], kernel_size_list[i], padding_size_list[i]) for i in range(len(channel_in_list))]
    
    layers += [nn.MaxPool2d(kernel_size = pooling_kernel_size,stride = pooling_stride)]
    
    return nn.Sequential(*layers)
  
# 将一个线性层、BN层和非线性层封装在一起
def vgg_fc_layer(size_in, size_out):
  
    layer = nn.Sequential(
        nn.Linear(size_in, size_out),
        nn.BatchNorm1d(size_out),
        nn.ReLU()
    )
    
    return layer

class VGG16(nn.Module):
    def __init__(self):
        super(VGG16, self).__init__()

        # 指定每一个VGG块的参数
        self.layer1 = vgg_conv_block([3,64], [64,64], [3,3], [1,1], 2, 2)
        self.layer2 = vgg_conv_block([64,128], [128,128], [3,3], [1,1], 2, 2)
        self.layer3 = vgg_conv_block([128,256,256], [256,256,256], [3,3,3], [1,1,1], 2, 2)
        self.layer4 = vgg_conv_block([256,512,512], [512,512,512], [3,3,3], [1,1,1], 2, 2)
        self.layer5 = vgg_conv_block([512,512,512], [512,512,512], [3,3,3], [1,1,1], 2, 2)

        # 过渡全连接层
        self.layer6 = vgg_fc_layer(7*7*512, 4096)
        self.layer7 = vgg_fc_layer(4096, 4096)

        # 最后的全连接层
        self.layer8 = nn.Linear(4096, 1000)

    def forward(self, x):
        out = self.layer1(x)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.layer4(out)
        out = self.layer5(out)
        out = out.view(out.size(0), -1)
        out = self.layer6(out)
        out = self.layer7(out)
        out = self.layer8(out)

        return out

def test():
    net = VGG16()
    x = torch.randn(2,3,224,224)
    y = net(x)
    print(y.size())

test()

torch.Size([2, 1000])

sum_ = 0
for name, param in net.named_parameters():
    mul = 1
    for size_ in param.shape:
        mul *= size_                          # 统计每层参数个数
    sum_ += mul                               # 累加每层参数个数
    #print('{} : {}' % (name, param.shape))  # 打印参数名和参数数量
print('参数个数：', sum_)

参数个数： 138382376