sklearn素线性回归及岭回归API介绍+模型的保存与加载
sklearn素线性回归及岭回归API介绍+模型的保存与加载
下面介绍一种线性回归训练模型的方法。线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
损失函数
总损失定义为: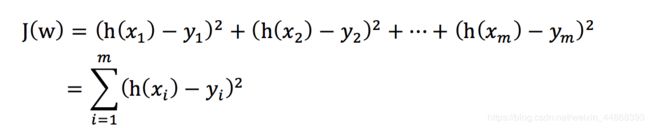
yi为第i个训练样本的真实值
h(xi)为第i个训练样本特征值组合预测函数
又称最小二乘法
优化算法:
1.正规方程
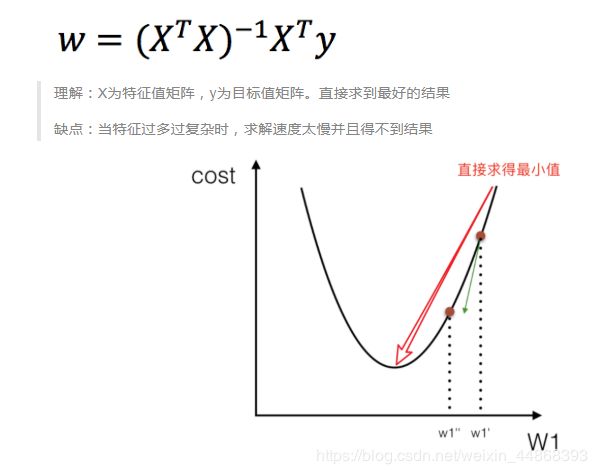
2.梯度下降法
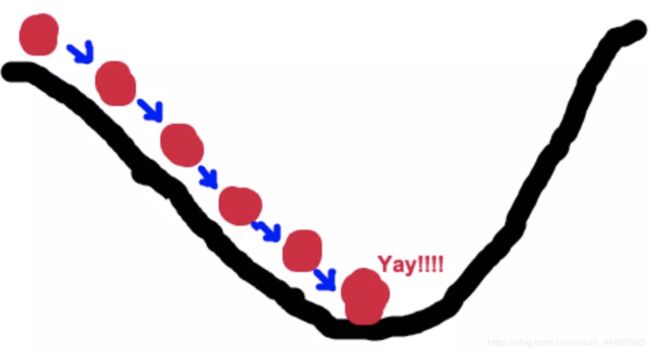
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。
我们的目标就是找到这个函数的最小值,也就是山底。
根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数值变化最快的方向。 所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。
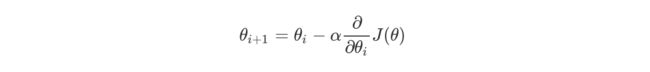
梯度下降和正规方程的对比:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高O(n3) |
全梯度下降算法(FG) 在进行计算的时候,计算所有样本的误差平均值,作为我的目标函数
随机梯度下降算法(SG) 每次只选择一个样本进行考核
小批量梯度下降算法(mini-batch) 选择一部分样本进行考核
随机平均梯度下降算法(SAG)会给每个样本都维持一个平均值,后期计算的时候,参考这个平均值
API代码:
sklearn.linear_model.LinearRegression(fit_intercept=True) 通过正规方程优化 参数
fit_intercept:是否计算偏置 属性 LinearRegression.coef_:回归系数
LinearRegression.intercept_:偏置
sklearn.linear_model.SGDRegressor(loss=“squared_loss”,
fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
SGDRegressor类实现了随机梯度下降学习,它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。 参数: loss:损失类型
loss=”squared_loss”: 普通最小二乘法 fit_intercept:是否计算偏置 learning_rate :
string, optional 学习率填充 ‘constant’: eta = eta0 ‘optimal’: eta = 1.0 /
(alpha * (t + t0)) [default] ‘invscaling’: eta = eta0 / pow(t,
power_t) power_t=0.25:存在父类当中
对于一个常数值的学习率来说,可以使用learning_rate=’constant’ ,并使用eta0来指定学习率。 属性:
SGDRegressor.coef_:回归系数 SGDRegressor.intercept_:偏置
实例:波士顿房价预测
from sklearn.datasets import load_boston #数据引入
from sklearn.model_selection import train_test_split #数据分割
from sklearn.preprocessing import StandardScaler #标准化
from sklearn.linear_model import LinearRegression #正规方程
from sklearn.linear_model import SGDRegressor #梯度下降法
from sklearn.metrics import mean_squared_error #均方误差
from sklearn.linear_model import Ridge #岭回归
from sklearn.externals import joblib #模型保存加载
import pandas as pd
import numpy as np
# 1.获取数据
data = load_boston()
# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)
# 3.特征工程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4.机器学习-线性回归(正规方程)
#estimator = LinearRegression() #正规方程
estimator = SGDRegressor(max_iter=1000) #梯度下降法
estimator.fit(x_train, y_train)
# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)
# 5.2 评价
# 均方误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)
new_dataframe = pd.DataFrame(columns = ['y_test','y_predict'])
new_dataframe['y_test'] = y_test
new_dataframe['y_predict'] = y_predict
线性回归的改进-岭回归
API
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver=“auto”, normalize=False)
具有l2正则化的线性回归
alpha:正则化力度,也叫 λ
λ取值:0~1 1~10
solver:会根据数据自动选择优化方法
sag:如果数据集、特征都比较大,选择该随机梯度下降优化
normalize:数据是否进行标准化
normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
Ridge.coef_:回归权重
Ridge.intercept_:回归偏置
Ridge方法相当于SGDRegressor(penalty=‘l2’, loss=“squared_loss”),只不过SGDRegressor实现了一个普通的随机梯度下降学习,推荐使用Ridge(实现了SAG)
sklearn.linear_model.RidgeCV(BaseRidgeCV, RegressorMixin)
具有l2正则化的线性回归,可以进行交叉验证
coef:回归系数
from sklearn.linear_model import Ridge #岭回归
def linear_model2():
"""
线性回归:岭回归
:return:
"""
# 1.获取数据
data = load_boston()
# 2.数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)
# 3.特征工程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4.机器学习-线性回归(岭回归)
estimator = Ridge(alpha=1)
# estimator = RidgeCV(alphas=(0.1, 1, 10)) #交叉验证
estimator.fit(x_train, y_train)
# 5.模型评估
# 5.1 获取系数等值
y_predict = estimator.predict(x_test)
print("预测值为:\n", y_predict)
print("模型中的系数为:\n", estimator.coef_)
print("模型中的偏置为:\n", estimator.intercept_)
# 5.2 评价
# 均方误差
error = mean_squared_error(y_test, y_predict)
print("误差为:\n", error)
linear_model2()
结果:
预测值为:
[28.13514381 31.28742806 20.54637256 31.45779505 19.05568933 18.26035004
20.59277879 18.46395399 18.49310689 32.89149735 20.38916336 27.19539571
14.82641534 19.22385973 36.98699955 18.29852297 7.78481347 17.58930015
30.19228148 23.61186682 18.14688039 33.81334203 28.44588593 16.97492092
34.72357533 26.19400705 34.77212916 26.62689656 18.63066492 13.34246426
30.35128911 14.59472585 37.18259957 8.93178571 15.10673508 16.1072542
7.22299512 19.14535184 39.53308652 28.26937936 24.62676357 16.76310494
37.85719041 5.71249289 21.17777272 24.60640023 18.90197753 19.95020929
15.1922374 26.27853095 7.55102357 27.10160025 29.17947182 16.275476
8.02888564 35.42165713 32.28262473 20.9525814 16.43494393 20.88177884
22.92764493 23.58271167 19.35870763 38.27704421 23.98459232 18.96691367
12.66552625 6.122414 41.44033214 21.09214394 16.23412117 21.51649375
40.72274345 20.53192898 36.78646575 27.01972904 19.91315009 19.66906691
24.59629369 21.2589005 30.93402996 19.33386041 22.3055747 31.07671682
26.39230161 20.24709071 28.79113538 20.85968277 26.04247756 19.25344252
24.9235031 22.29606909 18.94734935 18.83346051 14.09641763 17.43434945
24.16599713 15.86179766 20.05792005 26.51141362 20.11472351 17.03501767
23.83611956 22.82305362 20.88305157 36.10592864 14.72050619 20.67225818
32.43628539 33.17614341 19.8129561 26.45401305 20.97734485 16.47095097
20.76417338 20.58558754 26.85985053 24.18030055 23.22217136 13.7919355
15.38830634 2.78927979 28.87941047 19.80046894 21.50479706 27.53668749
28.48598562]
模型中的系数为:
[-0.63591916 1.12109181 -0.09319611 0.74628129 -1.91888749 2.71927719
-0.08590464 -3.25882705 2.41315949 -1.76930347 -1.74279405 0.87205004
-3.89758657]
模型中的偏置为:
22.62137203166228
误差为:
20.064724392806884
模型的保存和加载
API
from sklearn.externals import joblib
保存:joblib.dump(estimator,‘test.pkl’)
加载:estimator = joblib.load(‘test.pkl’)