牛顿法与梯度下降法求解实际问题对比

基于jupyter notebook的Python编程

– 牛顿法及梯度下降法原理和实际问题的解决

一、梯度下降法

1、梯度下降法基本原理

梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。梯度下降法的计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）。

二、利用梯度下降法求解多元函数及线性分析

1、利用梯度下降法求解多元函数极值

1).导入函数依赖库

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings

2).解决中文输出的问题

# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

3).写出二维原始函数和偏函数

# 二维原始图像
def f2(x, y):
    return x**2+2*(y)**2 - 4*(x)-2*(x)*(y)  
## 偏函数
def hx1(x, y):
    return 2*x-4-2*y
def hx2(x, y):
    return 4*y-2*x

X1 = np.arange(-4,4,0.2)
X2 = np.arange(-4,4,0.2)

X1, X2 = np.meshgrid(X1, X2) # 生成xv、yv，将X1、X2变成n*m的矩阵，方便后面绘图
Y = np.array(list(map(lambda t : f2(t[0],t[1]),zip(X1.flatten(),X2.flatten()))))
Y.shape = X1.shape # 1600的Y图还原成原来的（40,40）


x1 = 1
x2 = 1
alpha = 0.1
#保存梯度下降经过的点
GD_X1 = [x1]
GD_X2 = [x2]
GD_Y = [f2(x1,x2)]
# 定义y的变化量和迭代次数
y_change = f2(x1,x2)
iter_num = 0

4).通过循环，计算出最终的结果和迭代次数

while(y_change < 1e-10 and iter_num < 100) :
    tmp_x1 = x1 - alpha * hx1(x1,x2)
    tmp_x2 = x2 - alpha * hx2(x1,x2)
    tmp_y = f2(tmp_x1,tmp_x2)
 
    f_change = np.absolute(tmp_y - f2(x1,x2))
    x1 = tmp_x1
    x2 = tmp_x2
    GD_X1.append(x1)
    GD_X2.append(x2)
    GD_Y.append(tmp_y)
    iter_num += 1
print(u"最终结果为:(%.5f, %.5f, %.5f)" % (x1, x2, f2(x1,x2)))
print(u"迭代过程中X的取值，迭代次数:%d" % iter_num)
print(GD_X1)

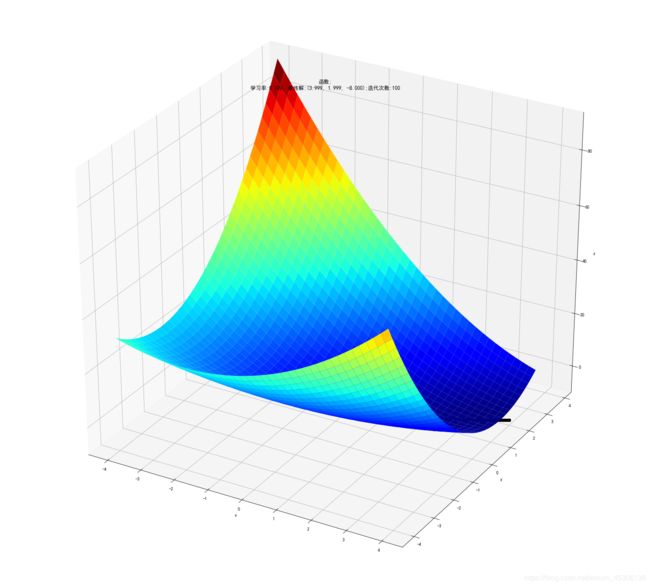
最终结果为:(3.99907, 1.99943, -8.00000)
迭代过程中X的取值，迭代次数:100
[1, 1.4, 1.68, 1.896, 2.0751999999999997, 2.2310399999999997, 2.3703679999999996, 2.4968576, 2.6126387199999996, 2.719076864, 2.8171465727999996, 2.90761138176, 2.9911114424319996, 3.0682070114303994, 3.1394007813324794, 3.2051500088360956, 3.2658736685842427, 3.321957132130058, 3.373755570805014, 3.421596660989794, 3.4657828742315058, 3.5065934930885985, 3.5442864256621753, 3.5790998589680623, 3.61125377526393, 3.6409513474235546, 3.6683802252768474, 3.693713722521222, 3.717111912407898, 3.7387226394617197, 3.7586824537869323, 3.7771174739385485, 3.7941441838477177, 3.8098701688538434, 3.824394795502385, 3.837809839407648, 3.8502000651496577, 3.861643761870156, 3.872213237952369, 3.8819752779104477, 3.8909915643755846, 3.899319067845221, 3.9070104066580527, 3.9141141794693763, 3.9206752723275837, 3.9267351422920918, 3.9323320793847913, 3.937501448530188, 3.9422759130129545, 3.9466856408648536, 3.950758495485095, 3.954520211698598, 3.957994558364595, 3.96120348856305, 3.964167278307848, 3.9669046546632454, 3.9694329140730904, 3.9717680316504986, 3.9739247621185383, 3.975916733039734, 3.977756530923471, 3.979455780755376, 3.9810252194511992, 3.9824747636993134, 3.983813572620511, 3.985050105641018, 3.9861921759444, 3.987246999840112, 3.9882212423606207, 3.9891210593752198, 3.9899521364866346, 3.990719724956192, 3.991428674884549, 3.9920834658576445, 3.9926882352515007, 3.9932468043747376, 3.993762702613972, 3.9942391897346763, 3.9946792764783994, 3.9950857435865013, 3.995461159370606, 3.9958078959407883, 3.996128144194037, 3.9964239276577045, 3.9966971152754103, 3.9969494332161846, 3.997182475781478, 3.9973977154789475, 3.9975965123266763, 3.99778012244661, 3.997949706001516, 3.9981063345256143, 3.9982509976951928, 3.9983846095819997, 3.9985080144289147, 3.998621991984401, 3.9987272624294388, 3.9988244909280777, 3.998914291830356, 3.998997232554144, 3.999073837170445]

5).作出二元函数的图像

# 作图
fig = plt.figure(facecolor='w',figsize=(20,18))
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(GD_X1,GD_X2,GD_Y,'ko-')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title(u'$ y = x1^2+2(x2)^2 - 4(x1)-2(x1) (x2) $')

ax.set_title(u'函数;\n学习率:%.3f; 最终解:(%.3f, %.3f, %.3f);迭代次数:%d' % (alpha, x1, x2, f2(x1,x2), iter_num))
plt.show()

2、利用梯度下降法求解二元线性回归方程

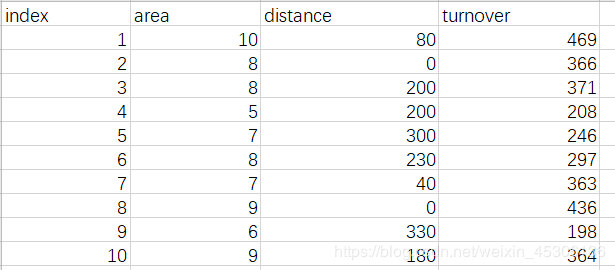
1).准备数据表

2).导入函数依赖库，读取数据，为变量赋值

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data=np.genfromtxt('F:/test.csv',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,2]

3).定义初始值，学习率和迭代次数

#定义a1，a2，b为方程y=a1x1+a2x2+b的系数，e为学习率
e=0.00001
a1=0
a2=0
b=0
#定义最大迭代次数
epochs=10000

4).代价函数

def compute_error(b,a1,a2,x_data,y_data):
    totalerror=0
    for i in range(0,len(x_data)):#定义一共有多少样本点
        totalerror=totalerror+(y_data[i]-(a1*x_data[i,0]+a2*x_data[i,1]+b))**2
    return totalerror/float(len(x_data))/2

5).利用梯度下降法求解回归系数

def gradient_descent_runner(x_data,y_data,b,a1,a2,e,epochs):
    m=len(x_data)
    for i in range(epochs):
        b_grad=0
        a1_grad=0
        a2_grad=0
        for j in range(0,m):
            b_grad-=(1/m)*(-(a1*x_data[j,0]+a2*x_data[j,1]+a2)+y_data[j])
            a1_grad-=(1/m)*x_data[j,0]*(-(a1*x_data[j,0]+a2*x_data[j,1]+b)+y_data[j])
            a2_grad-=(1/m)*x_data[j,1]*(-(a1*x_data[j,0]+a2*x_data[j,1]+b)+y_data[j])
        b=b-e*b_grad
        a1=a1-e*a1_grad
        a2=a2-e*a2_grad
    return b,a1,a2

6).输出各系数及回归方程

b,a1,a2=gradient_descent_runner(x_data,y_data,b,a1,a2,e,epochs)
print('结果：\n迭代次数：{0} 学习率：{1}  a0={2},a1={3},a2={4},代价函数:{5}'.format(epochs,e,b,a1,a2,compute_error(b,a1,a2,x_data,y_data)))
print("多元线性回归方程为:y=",a1,"X1+(",a2,")X2+",b)

结果：
迭代次数：10000 学习率：1e-05  a0=5.3774162274868,a1=45.0533119768975,a2=-0.19626929358281256,代价函数:366.7314528822914
多元线性回归方程为:y= 45.0533119768975 X1+( -0.19626929358281256 )X2+ 5.3774162274868

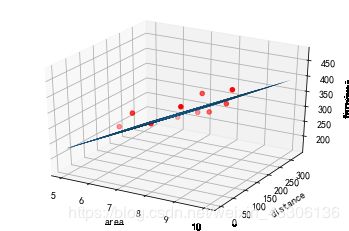
7).画出线性方程拟合图

ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o')
x0=x_data[:,0]
x1=x_data[:,1]
x0,x1=np.meshgrid(x0,x1)
z=b+a1*x0+a2*x1
ax.plot_surface(x0,x1,z)
ax.set_xlabel('area')
ax.set_ylabel('distance')
ax.set_zlabel("turnover")
plt.show()

二、牛顿法

1、牛顿法的基本原理

牛顿法是一种是用导数的算法，它每一步的迭代方向都是沿着当前点函数值下降的方向。

2、使用最小二乘法求解线性回归方程

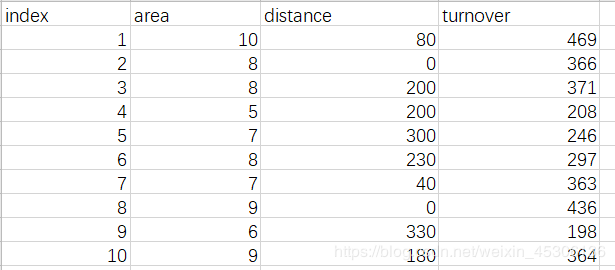
1).准备数据表

2).导入函数依赖库

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline

3).读取数据，并赋值

data=pd.read_excel("F:/test.xlsx")
X1=data['area'] #店铺面积
X2=data['distance'] #距车站的距离
Y=data['turnover'] #月营业额

4).矩阵转置

Y1=np.array([Y]).T #对矩阵y进行转置
X11=np.array([X1]).T
X22=np.array([X2]).T
A=np.array([[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]])
B=np.hstack((A,X11))
X=np.hstack((B,X22)) #矩阵化为一个矩阵
X_=X.T #矩阵x的转置
X_X=np.dot(X_,X) #矩阵x和X的转置矩阵的乘积
X_X_=np.linalg.inv(X_X) #将矩阵X和转置矩阵的乘积求逆矩阵

5).求解回归方程系数

W=np.dot(np.dot((X_X_),(X_)),Y1) #解依次为截距，a1和a2
b=W[0][0]
a1=W[1][0]
a2=W[2][0]
print("a1=",a1)
print("a2=",a2)
print("截距:",b)
print("多元线性回归方程: y=",a1,"*area+",a2,"*distance+",b)

a1= 41.51347825643848
a2= -0.34088268566362023
截距: 65.32391638894899
多元线性回归方程: y= 41.51347825643848 *area+ -0.34088268566362023 *distance+ 65.32391638894899

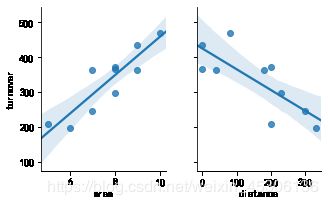
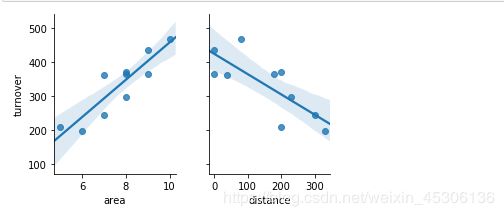
6).画出回归分析图

import seaborn as sns
data1=pd.read_excel('F:/test.xlsx')
sns.pairplot(data1,x_vars=['area','distance'],y_vars='turnover',height=3,aspect=0.8,kind='reg')
plt.show()

7).求解判定系数

sumturnover=0
y1=0
for i in range(0,len(Y)):
    sumturnover=sumturnover+Y[i] #求出月营业额的和
y1=sumturnover/len(Y) #月营业额的均值
#求营业额-营业额均值的和
y_y1=0
for i in range(0,len(Y)):
    y_y1=y_y1+(Y[i]-y1)
#求预测值
turnover=[]
for i in range(0,len(Y)):
    turnover.append(a1*X1[i]+a2*X2[i]+b)
y2=0
sumy2=0
for i in range(len(turnover)):
    sumy2=sumy2+turnover[i] #求出预测值的和
y2=sumy2/len(turnover) #求出预测值的均值
#求预测值-预测均值的和
y11_y2=0
for i in range(0,len(turnover)):
    y11_y2=y11_y2+(turnover[i]-y2)
#求营业额-营业额均值的平方和
Syy=0
for i in range(0,len(Y)):
    Syy=Syy+((Y[i]-y1)*(Y[i]-y1))
#预测营业额-预测额均值的平方和
Sy1y1=0
for i in range(0,len(turnover)):
    Sy1y1=Sy1y1+((turnover[i]-y2)*(turnover[i]-y2))
#求出Syy1
Syy1=0
for i in range(0,len(turnover)):
    Syy1=Syy1+((Y[i]-y1)*(turnover[i]-y2))
#根据R的求解公式，求解出R，进而求出R2
R=Syy1/((Syy*Sy1y1)**0.5)
R2=R*R
print("判定系数R2为:",R2)

判定系数R2为: 0.9452358526817115

三、牛顿法与梯度下降法的对比

对于同一线性回归方程分析求解系数及回归方程对比

最小二乘法求解结果

梯度下降法求解结果

原文参考地址1：https://blog.csdn.net/qq_42451251/article/details/105301522
原文参考地址2：https://blog.csdn.net/qq_42451251/article/details/105019128
原文参考地址3：https://blog.csdn.net/qq_35946969/article/details/84446000