魔法(【CCF】NOI Online能力测试 入门组第三题)
【题目描述】
C 国由 n 座城市与 m 条有向道路组成,城市与道路都从 1 开始编号,经过 i 号道路需要 ti 的费用。
现在你要从 1 号城市出发去 n 号城市,你可以施展最多 K 次魔法,使得通过下一条道路时,需要的费用变为原来的相反数,即费用从 ti 变为 -ti。请你算一算,你至少要花费多少费用才能完成这次旅程。注意:使用魔法只是改变一次的花费,而不改变一条道路自身的 ti;最终的费用可以为负,并且一个城市可以经过多次(包括 n 号城市)。
【输入格式】
从文件 magic.in 中读入数据。
第一行三个整数 n, m, K,表示城市数、道路数、魔法次数限制。
接下来 m 行每行三个整数 ui,vi,ti,第 i 行描述 i 号道路,表示一条从 ui 到 vi 的有向道路,经过它需要花费 ti。
【输出格式】
输出到文件 magic.out 中。
仅一行一个整数表示答案。
【样例1输入】
4 3 2
1 2 5
2 3 4
3 4 1
【样例1输出】
-8
【样例1解释】
依次经过 1 号道路、2 号道路、3 号道路,并在经过 1、2 号道路前使用魔法。
【样例2输入】
2 2 2
1 2 10
2 1 1
【样例2输出】
-19
【样例2解释】
依次经过 1 号道路、2 号道路、1 号道路,并在两次经过 1 号道路前都使用魔法。
【数据范围与提示】
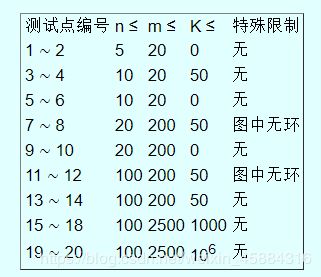
对于所有测试点和样例满足:
1 ≤ n ≤ 100,1 ≤ m ≤ 2500,0 ≤ K ≤ 106,1 ≤ ui,vi ≤ n,1 ≤ ti ≤ 109。
数据保证图中无自环,无重边,至少存在一条从 1 号城市到达 n 号城市的路径。
分析
k=0
直接跑Floyd 即可得出结果(传送门:Floyd算法)
k=1
设 f k,i,j 表示在使用不超过 k次魔法的情况下,从 i 到 j 的最短路。
现在我们知道了 f 0,i,j,如何得到 f 1,i,j呢?
边的规模只有 2500,我们可以直接枚举要用魔法的边,转移时强制走这条边,求最短路。
假如边 (u,v,w)用了魔法,转移方程如下:
f{1,i,j}=\min{f{0,i,j},\min f{0,i,u}+f{0,v,j}-w}
k=2
我们已经得到了 k=1k=1 的情况,如何推 k=2k=2 的情况呢?
类似于 Floyd,我们可以枚举一个中转点 k,i→k 最多用一次魔法,k→j 最多用一次魔法,合并起来就是最多两次魔法的答案了。
写成式子长这样:
f{2,i,j}=\min f{1,i,k}+f_{1,k,j}
这个可以用矩阵快速幂来优化转移,最多用 i 次魔法的结果和最多用 j次魔法的结果按照上面的转移方式合并的话,可以得到最多用 i+j 次魔法的结果