特征选择 ReliefF算法

一、算法

      Relief算法最早由Kira提出. 基本内容：从训练集D中随机选择一个样本R, 然后从和R同类的样本中寻找k最近邻样本H，从和R不同类的样本中寻找k最近邻样本M， 最后按照公式更新特征权重.

    算法:

        1.置0所有特征权重

        2.For i=1 to m do

            2.1 随机选择一个样本

            2.2 从同类中找到R的k最近邻样本H，从不同类中找到R的k最近邻样本M.

            2.3 for i=1 to N do

                

             2.4 对W进行排序

 

二、Matlab实现

    主函数Main.m

%主函数
function main
clear;clc;
load A:\Data\data.txt%加载数据
D=data(:,2:size(data,2));%排除编号的一列
m=80; %抽样次数
k=8; %k近邻
N=20; %运行次数
for i=1:N
    W(i,:)=RelifF(D,m,k);
end
for i=1:N %将每次计算的权重进行绘图
    plot(1:size(W,2),W(i,:));%size(A,1)获取A矩阵行数，size(A,2)获取A矩阵列数
    hold on
end
for i=1:size(W,2) %计算N次中，每个属性的平均值
    result(1,i)=sum(W(:,i))/size(W,1);
end
xlabel('属性编号');
ylabel('特征权重');
title('ReliefF算法计算特征权重')
axis([1 10 0 0.3])
%-----绘制每一种属性变化趋势-----------%
name=char('块厚度','细胞大小均匀性','细胞形态均匀性','边缘粘附力','单上皮细胞尺寸','裸核','Bland染色质','正常核仁','核分裂');
name=cellstr(name);%cellstr(name)将字符串转化为元胞数组
for i=1:size(W,2)
    figure
    plot(1:size(W,1),W(:,i))
    xlabel('计算次数');
    ylabel('特征权重');
    title([char(name(i)) '(属性' num2str(i) ')的特征权重变化'])%title中[]来连接字符串,num2str(i)将数字i转化为 
end

该程序进行N次调用Reliff函数来获取W的行矩阵，该行矩阵是所有特征的权重

接着对得到的N次结果进行绘图

然后把N次结果取平均值作为最终的特征权重结果保存在result中

最后对之前的的统一绘图，变成单一绘图

 

Reliff.m

%Relief函数实现
%D为输入的训练集合，输入集合去掉身份信息;k为最近邻样本个数
function W=RelifF(D,m,k)
Rows=size(D,1); %样本个数
Cols=size(D,2); %特征个数
%将数据分成两类，加快计算速度
D1=zeros(0,Cols);%第一类,0行 []
D2=zeros(0,Cols);%第二类
for i=1:Rows
    if D(i,Cols)==2 %良性
        D1(size(D1,1)+1,:)=D(i,:);%matlab变量弱类型可以动态修改
    elseif D(i,Cols)==4 %不是良性
        D2(size(D2,1)+1,:)=D(i,:);
    end
end %分好类填入D1和D2中
W=zeros(1,Cols-1);%初始化特征权重，置为0
for  i=1:m %选择循环操作
    %从D中随机选择一个样本R
    [R,Dh,Dm]=GetRandSamples(D,D1,D2,k);
    %更新特征权重
    for j=1:length(W)
        W(1,j)=W(1,j)-sum(Dh(:,j))/(k*m)+sum(Dm(:,j))/(k*m);%按照公式这里的sum就是上面公式中从1到k的求和，因为Dh和Dm是k行
                                            %sum不仅可以对矩阵求和，还能对矩阵元素满足条件的元素求和，比如sum(D(:,size(D,2)==2)
                                            %这样只对D的最后一列是2的累计加1
    end
end 

该程序首先分了两类D1和D2,然后将D中的对应类复制到D1和D2中

接着依据分好的类去得到样本和特征差Dh,Dm

按照公式进行更新W

 

GetRandSamples.m

%获取随机R 找出邻近样本
%D:训练集 D1:类别1数据集 D2:类别2数据集
%Dh 与R同类相邻样本距离; Dm:与R不同类的相邻样本距离
function [R,Dh,Dm]=GetRandSamples(D,D1,D2,k)
%先随机产生一个随机数，确定选定的样本R
r=ceil(1+(size(D,1)-1)*rand);
R=D(r,:);%将第r行选中赋值给R
d1=zeros(1,0);%置0,d1,d2是与R的距离,0列 []
d2=zeros(1,0);
%D1,D2已经分好类了
for i=1:size(D1,1) %计算R与D1的距离
    d1(1,i)=norm(R-D1(i,:)); %norm用来求两个向量之间的距离,即求R和D1中每行的距离放入对应d1行中
end
for j=1:size(D2,1) %计算R与D2的距离
    d2(1,j)=norm(R-D2(j,:));
end
[v1,L1]=sort(d1);%对d1,d2进行排序,这里v1是排行序的结果,L1是现在排好序的位置处的元素原本是在哪个位置上的，即建立了原来和现在元素索引的一种映射 
[v2,L2]=sort(d2);
if R(1,size(R,2))==2 %如果样本R=2是良性
    H=D1(L1(1,2:k+1),:); %L1中是与R最近距离的变化，赋给H,除去自身的，因为第一个是R，不能加入
    M=D2(L2(1,1:k),:);%
else
    %之前版本
    %H=D1(L1(1,1:k),:); 
    %M=D2(L2(1,2:k+1),:);%同上面的if中的H

    %更改版本, 依据公式，这里H和M分别表示和R的同类与不同类的样本集。由于R的变化，所以这里H和M相比较之前的需要互换下位置
    M=D1(L1(1,1:k),:); 
    H=D2(L2(1,2:k+1),:);%同上面的if中的H
end
%循环计算2个样本特征之间的特征距离
for i=1:size(H,1)
    for j=1:size(H,2)
        Dh(i,j)=abs(H(i,j)-R(1,j))/9; %公式进行求得diff值,因为A连续从1到10
        Dm(i,j)=abs(M(i,j)-R(1,j))/9;
    end
end%(R特征-Mk特征)/(max-min)
     

该程序首先初始化两个距离行向量，保存从R到D1和D2每行的距离.

接着对距离进行归一化(或者称按照公式)得到diff值,用于后面的W更新

 

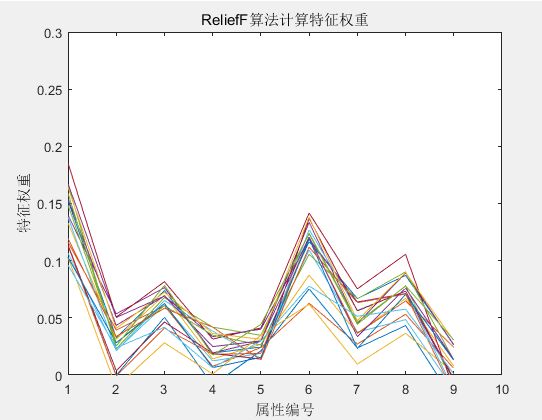
三、运行结果

    

可见第一个和第六个特征影响很大，第九个影响很小.

 

参考:

    https://blog.csdn.net/ferrarild/article/details/18792613

数据来源:

    http://archive.ics.uci.edu/ml/