基于SVD协同过滤算法实现的电影推荐系统

一、数据获取

将数据集下载并保存在本地
http://files.grouplens.org/datasets/movielens/ml-100k.zip 解压到项目文件下
其中u.data文件包含完整的数据集，README 是对整个数据文件的介绍，从中可以得知u.data中的列依次为:
user id|item id|rating|timestamp 这里的物品是指电影

二、基于item的协同过滤推荐

step1 导入模块 数据

from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'
%matplotlib inline
import numpy as np
import pandas as pd
header = ['user_id','item_id','rating','timestamp']
src_data = pd.read_csv('./datas/ml-100k/u.data',sep = '\t',names = header)
src_data.head() 

step2 数据清洗 拆分数据集

src_data.user_id.nunique                    #查看用户去重个数
src_data.item_id.nunique                    #查看物品去重个数
src_data.duplicated(subset = ['user_id','item_id']).sum()  #检查是否有重复的用户物品打分记录

item_id_userent = src_data\                 #每个物品对应的客户数
                  .groupby('item_id')\
                  .count()['user_id'] 

import matplotlib.pyplot as plt 
plt.rcParams["font.sans-serif"]=['SimHei']  # 用于正常显示中文标签
plt.rcParams['axes.unicode_minus']=False    # 用来正常显示负号

plt.hist(item_id_userent.values)            # 通过直方图观看
plt.xlabel("客户人数")
plt.ylabel("评论的电影个数")
plt.plot() 

#每个物品对应的客户数（10分位，20分位...100分位数）
item_id_userent.quantile(q = np.arange(0,1.1,0.1))  

#去重并赋值
n_users = src_data.user_id.nunique()
n_items = src_data.item_id.nunique()

# 训练集、测试集分离
from sklearn.model_selection import train_test_split
train_data, test_data = train_test_split(src_data, test_size=0.3)

user_item_matrix = np.zeros((n_users,n_items))                #构建用户物品矩阵
for line in src_data.itertuples():                            #以元组的方式赋值
    user_item_matrix[line[1]-1,line[2]-1] = line[3]

user_item_matrix.nonzero()[1]                                 #查看非零矩阵 
sparsity = round(len(user_item_matrix\
                     .nonzero()[1])/float(n_users*n_items),3) #检验矩阵稀疏性

step3 计算用户相似度矩阵—使用余弦距离

from sklearn.metrics.pairwise import pairwise_distances

item_similarity_m = pairwise_distances\
                    (user_item_matrix.T,metric = 'cosine')     #使用余弦距离
item_similarity_m.shape                                        #物品相似度矩阵=行列 
item_similarity_m[0:5,0:5].round(2)                            #相似度矩阵为对称矩阵(保留两位数字)

round(np.sum(item_similarity_m > 0)/float\
             (item_similarity_m.shape[0]*\
             tem_similarity_m.shape[1]),3)                     #非0值比例 

#分析上三角：得到等分位数(上三角函数 np.triu)
item_similarity_m_triu = np.triu(item_similarity_m,k = 1)      #对角线0右边的三角矩阵
item_sim_nonzero = np.round(item_similarity_m_triu\
                            [item_similarity_m_triu.nonzero()],3)
np.percentile(item_sim_nonzero,np.arange(0,101,10))            #得出相似度大，没有区分性  


#3.1得到预测矩阵
user_item_prediction = user_item_matrix\
                       .dot(item_similarity_m)/np\
                       .array([np.abs(item_similarity_m)\
                       .sum(axis=1)])  

step4 训练与预测

# 只取预测数据集中有评分的数据集，进行评估
from sklearn.metrics import mean_squared_error
from math import sqrt
prediction_flatten = user_item_prediction[user_item_matrix.nonzero()] 
user_item_matrix_flatten = user_item_matrix[user_item_matrix.nonzero()]

sqrt(mean_squared_error(prediction_flatten,       # 评估指标：RMSE 
                        user_item_matrix_flatten))  

test_data_matrix = np.zeros((n_users,n_items))    # 测试数据集构建
for line in test_data.itertuples():
    test_data_matrix[line[1]-1,line[2]-1 ]= line[3]  

item_prediction = user_item_matrix\               # 预测矩阵 
                  .dot(item_similarity_m) / np\
                  .array([np.abs(item_similarity_m).sum(axis=1)]) 

# 只取有评分的数据集预测
from sklearn.metrics import mean_squared_error
from math import sqrt
prediction_flatten = item_prediction[test_data_matrix.nonzero()] 
test_data_matrix_flatten = test_data_matrix[test_data_matrix.nonzero()]
sqrt(mean_squared_error(prediction_flatten, test_data_matrix_flatten))

#单模型结果提升思路-----改变相似度算法--余弦近距离->欧式距离
item_similarity_m = pairwise_distances(user_item_matrix.T,metric = 'euclidean')
#增加训练数据
train_data,test_data = train_test_split(src_data,test_size = 0.2)

三、基于SVD的协同过滤推荐

from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
import numpy as np
import pandas as pd
header = ['user_id', 'item_id', 'rating', 'timestamp']
src_data = pd.read_csv('ml-100k/u.data', sep='\t', names=header)
src_data.head()

用户-物品矩阵——数据集拆分

n_users = src_data.user_id.nunique()                   # 用户、物品数去重统计
n_items = src_data.item_id.nunique() 

from sklearn.model_selection import train_test_split  # 训练集、测试集拆分
train_data, test_data = train_test_split(src_data, test_size=0.3)

train_data_matrix = np.zeros((n_users, n_items))      # 训练集 用户-物品矩阵
for line in train_data.itertuples():
    train_data_matrix[line[1]-1, line[2]-1] = line[3] 

test_data_matrix = np.zeros((n_users, n_items))       # 测试集 用户-物品矩阵 
for line in test_data.itertuples():
    test_data_matrix[line[1]-1, line[2]-1] = line[3]

SVD分解，选择K

import scipy.sparse as sp
from scipy.sparse.linalg import svds

u, s, vt = svds(train_data_matrix, k = 20)     #获取奇异值分解因子。选择K.
s_diag_matrix=np.diag(s)
svd_prediction = np.dot(np.dot(u, s_diag_matrix), vt) 

u.shape                                        #数据感知
s.shape
vt.shape
s_diag_matrix.shape
svd_prediction.shape 

#np.cumsum([1,2,3,4,5,6])->array([ 1,  3,  6, 10, 15, 21], dtype=int32)
k=942                                          
u, s, vt = svds(train_data_matrix, k)
scumrate = pd.DataFrame({'cumsum':np.cumsum(s[::-1])/np.sum(s)}) 

# 查看预测矩阵值分布
pd.Series(np.percentile(svd_prediction, np\
                        .arange(0, 101, 10)))\
                        .map("{:.2f}".format)
# 查看训练数据矩阵值分布
pd.Series(np.percentile( train_data_matrix, np\
                        .arange(0, 101, 10)))\
                        .map("{:.2f}".format)
# 查看训练数据矩阵非0值分布
pd.Series(np.percentile( train_data_matrix[train_data_matrix.nonzero()], 
                        np.arange(0, 101, 10))).map("{:.2f}".format) 

svd_prediction[svd_prediction<0] = 0       # 将预测值中小于0的值，赋值为0
svd_prediction[svd_prediction>5] = 5       # 将预测值中大于5的值，赋值为5

训练 与 预测

# 训练集预测------只取预测数据集中有评分的数据集，进行评估
from sklearn.metrics import mean_squared_error
from math import sqrt
prediction_flatten = svd_prediction[train_data_matrix.nonzero()] 
train_data_matrix_flatten = train_data_matrix[train_data_matrix.nonzero()]
sqrt(mean_squared_error(prediction_flatten, train_data_matrix_flatten)) 

# 测试集预测------只取预测数据集中有评分的数据集
from sklearn.metrics import mean_squared_error
from math import sqrt
prediction_flatten = svd_prediction[test_data_matrix.nonzero()] 
test_data_matrix_flatten = test_data_matrix[test_data_matrix.nonzero()]
sqrt(mean_squared_error(prediction_flatten, test_data_matrix_flatten))

Top评分评估

有时间需要给客户推荐最喜欢的topk个物品，这时候需要按照得分从高到低选出topk个物品 这时候评估指标可以只准确率与召回率 预测集合中考察每个用户的TOPK物品 测试集中评分大于平均数的物品都认为是用户感兴趣的物品 准确率：P为预测集，T为测试集

ACC(P,T)=|P⋂T||P| A C C ( P , T ) = | P ⋂ T | | P |

召回率：P为预测集，T为测试集: ACC(P,T)=|P⋂T||P| A C C ( P , T ) = | P ⋂ T | | P |

集合相似度算法：Jaccard(杰卡德)相似性系数: J(A,B)=|A⋂B||A⋃B| J ( A , B ) = | A ⋂ B | | A ⋃ B |

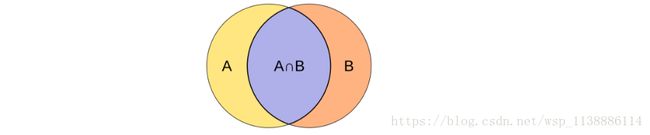
## 实际推荐过程中，需要在预测集中过滤掉已经评级过的物品
svd_p_df = pd.DataFrame(svd_prediction)
svd_p_df = svd_p_df[pd.DataFrame(train_data_matrix) == 0]  # 只选择在训练集没有被评过分的部分 

# 利用分位数函数获取每个用户的得分最高的topk个物品
topk = 10                                    # 看top10的相似
quantile = 1-topk/float(svd_p_df.shape[1])  # topk的分位数 

## 预测矩阵的topk 0,1矩阵
# 每行(每个用户)的topk分位数值
# 如果topk分位数值为0,则意味此行大于0的列数
topk_threshold = svd_p_df.quantile(q=quantile, axis=1).map(lambda x: max(x, 0.00000000000001))
# 对每行中前topk的数值标记为1，否则标记为0
svd_p_topk = svd_p_df.sub(topk_threshold, axis=0).applymap(lambda x:1 if x>=0 else 0) 

## 测试矩阵的topk 0,1矩阵
test_data_m_df = pd.DataFrame(test_data_matrix)
# 每行(每个用户)的topk分位数值
# 如果topk分位数值为0,则意味此行大于0的列数
topk_threshold = test_data_m_df.quantile(q=quantile, axis=1).map(lambda x: max(x, 0.000000001))
# 对每行中前topk的数值标记为1，否则标记为0
test_data_m_topk = test_data_m_df.sub(topk_threshold, axis=0).applymap(lambda x:1 if x>=0 else 0) 

# 并集矩阵
inter_m = test_data_m_topk*svd_p_topk

# Jaccard相似性
inter_m.sum().sum() / np.double(test_data_m_topk.sum().sum() + svd_p_topk.sum().sum() - inter_m.sum().sum())

# 准确率计算
inter_m.sum().sum() / np.double(svd_p_topk.sum().sum())

# 召唤率计算
inter_m.sum().sum() / np.double(test_data_m_topk.sum().sum())

基于user 的协同过滤推荐

from sklearn.metrics.pairwise import pairwise_distances
user_similarity_m = pairwise_distances(train_data_matrix, metric='cosine') 

#数据探索与感知 
user_similarity_m.shape                             # 物品相似矩阵 行列
round(np.sum(user_similarity_m>0)/float\            # 非0值比例
      (user_similarity_m.shape[0]*user_similarity_m.shape[1]),3) 
user_similarity_m[0:5, 0:5].round(2)                # 相似矩阵为对称矩阵 

# 现在我们只分析上三角，得到等分位数
user_similarity_m_triu = np.triu(user_similarity_m, k=1) 
item_sim_nonzero = np.round(user_similarity_m_triu[user_similarity_m_triu.nonzero()], 3)
np.percentile(item_sim_nonzero, np.arange(0,101,10)) 

# 得到预测矩阵P  添加新维度
mean_user_rating = train_data_matrix.mean(axis=1)
ratings_diff = (train_data_matrix - mean_user_rating[:, np.newaxis]) 
user_prediction = mean_user_rating[:, np.newaxis] + \
    user_similarity_m.dot(ratings_diff) / np.array([np.abs(user_similarity_m).sum(axis=1)]).T

训练 与 预测

# 只取预测数据集中有评分的数据集，进行评估
from sklearn.metrics import mean_squared_error
from math import sqrt
prediction_flatten = user_prediction[train_data_matrix.nonzero()] 
train_data_matrix_flatten = train_data_matrix[train_data_matrix.nonzero()]
sqrt(mean_squared_error(prediction_flatten, train_data_matrix_flatten)) 

# 测试数据集构建
test_data_matrix = np.zeros((n_users, n_items))
for line in test_data.itertuples():
    test_data_matrix[line[1]-1, line[2]-1] = line[3] 

# 只取预测数据集中有评分的数据集
from sklearn.metrics import mean_squared_error
from math import sqrt
prediction_flatten = user_prediction[test_data_matrix.nonzero()] 
test_data_matrix_flatten = test_data_matrix[test_data_matrix.nonzero()]
sqrt(mean_squared_error(prediction_flatten, test_data_matrix_flatten))