基于粒子滤波的定位算法 ——原理、理解与仿真

1 算法原理

1.1 机器人定位问题

关于机器人定位，有三大问题，它们分别是：

(1)“全局定位”：指初始位置未知，机器人靠自身运动确定自己在地图中的位姿。

(2)“位姿跟踪”：指已知自身位姿或者已经通过“全局定位”得到了一个较好的位姿估计，在后续运动时补偿精度较差的运动控制误差；

(3)“绑架劫持”：指机器人在已知自身位姿的情况下，得到了一个错误的位姿信息或者外界将其放到另外一个位姿，而里程计信息给出了错误的信息甚至没有给出控制信息。

1.2 粒子滤波步骤(可结合2中例题)

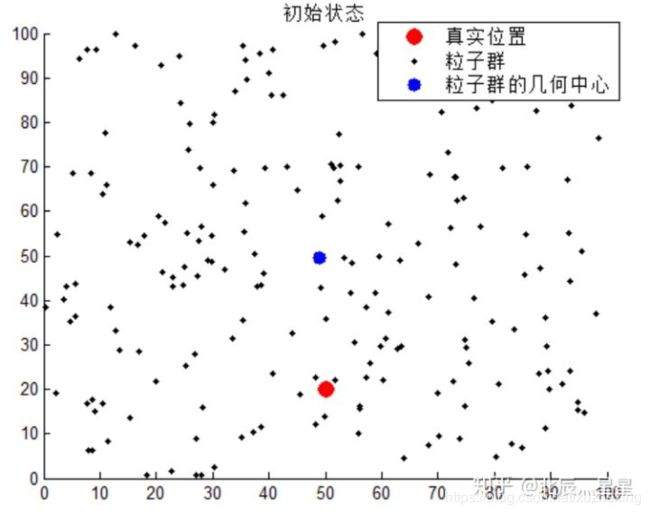
(1)初始状态：用大量粒子模拟运动状态，使粒子在空间内均匀分布；

(2)预测阶段：根据状态转移方程，将每一个粒子带入，得到一个预测粒子；

(3)校正阶段：对预测粒子进行评价（计算权重），越接近于真实状态的粒子，其权重越大；

(4)重采样：根据粒子权重对粒子进行筛选，筛选过程中，既要大量保留权重大的粒子，又要有一小部分权重小的粒子；

(5)滤波：将重采样后的粒子带入状态转移方程得到新的预测粒子，即步骤(2)。

2 一个二维定位的例子 (基于粒子滤波的定位算法)

2.1 问题

在二维空间，假设运动小车的初始位置、状态方程(运动预测方程)、传感器测量数据，用粒子滤波方法进行对其进行定位。

2.2 预设参数

(1)粒子总数N=200;

(2)运动时间T=10秒，且假设每秒进行一步动作;

(3)运动场地大小WorldSizeWorldSize=100100平方米;

(4)控制小车运动的方程，小车沿着某曲线运动(但实际的运动情况肯定和给的控制有些差别，这理解为叠加在理想运动方程上的控制误差，控制误差假设为5米)；

(5)传感器测量的小车位置数据同样也和实际情况不一致，这也可以理解为叠加在真实位置上的测量误差，测量误差假设为5米；

(6)小车初始位置已知，假设处在100*100场地中的（50,20)位置；

2.3 步骤与理解分析

(1)初始化粒子群

在整个场地内，将总粒子数N进行均匀分布，得到如图所示结果。

(2)小车开始运动(同时每运动一步进行一次测量)

小车按照控制给定的叠加了控制噪声的运动方程进行运动，运动达到下一位置后，传感器对当前位置进行测量，并得到一个测量的位置(不准确,含有测量噪声)

(3)粒子群更新(预测步骤)

把粒子群中的全部粒子逐个带入小车的运动方程中，得到粒子群的下一步位置。同时，计算此时每个粒子的位置和测量得到的小车位置 这两个位置之间的几何距离，按照距离的不同给每个粒子添加一个权重，用于重采样。显然，距离越近，权重越大（权重和距离关系的函数，这里采用高斯分布钟形曲线的右侧，即随距离增大，权重单调递减）。下一步，得到全部粒子的权重后，将它们进行归一化。

(4)重采样

对于全部M个粒子，它们的归一化权重集合为 \omega ，第 i 个粒子的权重为 \omega[i] 。则重采样过程可理解为旋转轮盘抽奖。如下图。

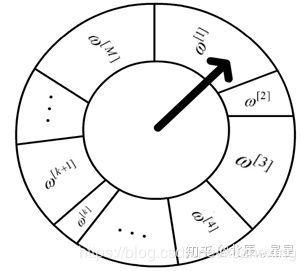
由于不同粒子的归一化权重不同，它们占轮盘的面积也不同，因此权重大的粒子更容易被抽中。

现在，我们需要重采样得到新的M个粒子组成的粒子群。因此，我们按照上述轮盘，抽M次，抽到某个权重 \omega[i] ，则把该权重对应的粒子放入新的M个粒子组成的粒子群中。这样，那些权重大的粒子可能被反复抽到，从而重复出现在新的粒子群中，而那些权重小的粒子可能会在新的粒子群中被丢弃。

某一次运动过程结束后，可画出小车实际位置、重采样后粒子群位置、以及粒子群的几何中心位置，如图所示。

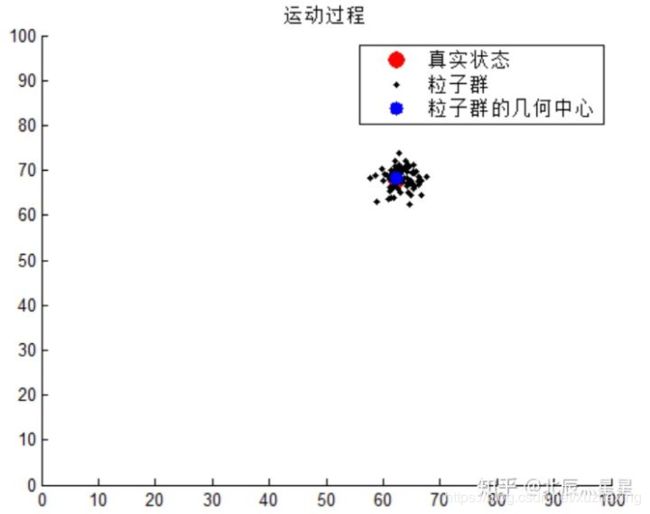
(5)重复步骤(2)~(4)，直到结束。

最后，我们可以得到整个运动过程中，小车实际路径、测量得到的路径、粒子群中心位置构成的路径，如图所示。

另外，还可以得到测量位置与真实位置间的误差，以及粒子群中心位置与真实位置间的误差，如图所示。

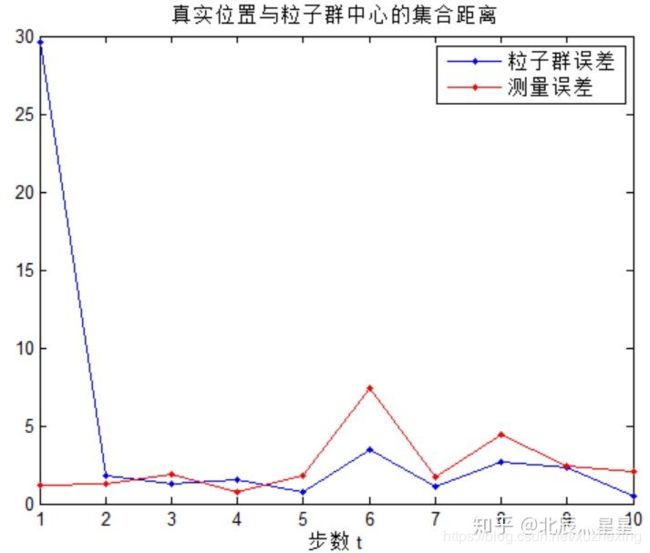
简单分析可知，综合控制和测量，利用粒子滤波进行定位，较单纯相信测量而言，更加精确。

2.4 本例的MATLAB源代码（附有详细注释）

%粒子滤波(定位运动轨迹)
%在二维空间,假设运动物体的一组(非线性)运动位置、速度、加速度数据,用粒子滤波方法进行处理
clc,clear,close all
%% 参数设置
N = 200; %粒子总数
Q = 5; %过程噪声(控制误差)  状态转移方程中使用
R = 5; %测量噪声  由真实位置叠加测量噪声得到测量位置
T = 10; %测量时间(总步数)
theta = pi/T; %旋转角度
distance = 80/T; %每次走的距离(步长)
WorldSize = 100; %世界大小
X = zeros(2, T); %存储系统状态(每列存储二维位置坐标(x,y),共T个位置)
Z = zeros(2, T); %存储系统的观测状态(每列存储二维位置坐标(x,y),共T次测量)
P = zeros(2, N); %建立粒子群(每列存储当前粒子的二维位置坐标,共N个粒子)
PCenter = zeros(2, T); %所有粒子的中心位置
w = zeros(N, 1); %每个粒子的权重
err = zeros(2,T); %误差(第一行为粒子与真实路径误差  第二行为测量与真实路径误差)
X(:, 1) = [50; 20]; %初始系统状态 即初始位置在坐标(50,20)
Z(:, 1) = X(:,1) + wgn(2,1,10*log10(R)); %初始系统的观测状态(为真实位姿叠加高斯噪声)
                                             %y = wgn(m,n,p) 产生一个m行n列的高斯白噪声的矩阵，p以dBW为单位指定输出噪声的强度
%% 初始化粒子群
for i = 1 : N
    P(:, i) = [WorldSize*rand; WorldSize*rand];%随机产生第i个粒子的坐标(rand为产生[0,1]之间均匀分布)
    dist = norm(P(:, i)-Z(:, 1)); %与测量位置相差的距离
    %求权重 (权重与距离的关系 为 均值是0,方差是sqrt(R)的高斯分布曲线)  因为均值为0且距离大于0 因此权重随着距离增加沿高斯曲线右侧递减
    w(i) = (1 / sqrt(R) / sqrt(2 * pi)) * exp(-(dist)^2 / 2 / R); 
end
PCenter(:, 1) = sum(P, 2) / N;%t=1时刻(初始时刻)所有粒子的几何中心位置
% 初始状态(t=1)画图
err(1,1) = norm(X(:, 1) - PCenter(:, 1));%粒子群几何中心与系统真实状态的误差
err(2,1) = wgn(1, 1, 10*log10(R));
figure(1);
hold on
set(0,'defaultfigurecolor','w')
plot(X(1, 1), X(2, 1), 'r.', 'markersize',30) %真实的初始状态位置(红点表示)
%grid on
axis([0 100 0 100]);
set(gca,'XTick',0:10:100) %改变x轴坐标间隔显示 这里间隔为10
set(gca,'YTick',0:10:100) %改变y轴坐标间隔显示 这里间隔为10
plot(P(1, :), P(2, :), 'k.', 'markersize',5); %各个粒子位置(N个黑点)
plot(PCenter(1, 1), PCenter(2, 1), 'b.', 'markersize',25); %所有粒子的中心位置(蓝点表示)
legend('真实位置', '粒子群', '粒子群的几何中心');
title('初始状态');
hold off
%% 开始运动
for k = 2 : T %从t=2到T
    %模拟一个弧线运动的状态
    X(:, k) = X(:, k-1) + distance * [(-cos(k * theta)); sin(k * theta)] + wgn(2, 1, 10*log10(Q)); %状态方程
    Z(:, k) = X(:, k) + wgn(2, 1, 10*log10(R)); %观测方程(状态上叠加测量的高斯噪声) 
    %粒子滤波
    %预测
    for i = 1 : N
        P(:, i) = P(:, i) + distance * [-cos(k * theta); sin(k * theta)] + wgn(2, 1, 10*log10(Q));%粒子群带入状态方程
        dist = norm(P(:, i)-Z(:, k)); %粒子群中各粒子 与 测量位置 的距离
        w(i) = (1 / sqrt(R) / sqrt(2 * pi)) * exp(-(dist)^2 / 2 / R); %求权重(距离近权重大)
    end
    %归一化权重
    wsum = sum(w);
    for i = 1 : N
        w(i) = w(i) / wsum;
    end
    %重采样（更新）
    for i = 1 : N
        wmax = 2 * max(w) * rand; %另一种重采样规则
        index = randi(N, 1);%生成一个在[1(默认值),N]之间均匀分布的伪随机整数
        while(wmax > w(index))
            wmax = wmax - w(index);
            index = index + 1;
            if index > N
                index = 1;
            end 
        end
        Pnext(:, i) = P(:, index); %得到新粒子放入临时集Pnext
    end
    P=Pnext;%用临时集Pnext更新粒子集P
    PCenter(:, k) = sum(P, 2) / N; %重采样后所有粒子的中心位置
    %计算误差
    err(1,k) = norm(X(:, k) - PCenter(:, k)); %粒子几何中心与系统真实状态的误差
    err(2,k) = norm(X(:, k) - Z(:, k));
    %画图
    figure(2);
    set(0,'defaultfigurecolor','w')
    clf;%清空figure(2)中的图像 以便循环重新画
    hold on
    plot(X(1, k), X(2, k), 'r.', 'markersize',30); %系统状态位置
    plot(P(1, :), P(2, :), 'k.', 'markersize',5); %各个粒子位置
    plot(PCenter(1, k), PCenter(2, k), 'b.', 'markersize',25); %所有粒子的中心位置
    axis([0 100 0 100]);
    title('运动过程');
    legend('真实状态', '粒子群', '粒子群的几何中心');
    hold off
    pause(0.1);%停0.1s开始下次迭代
end
%% 绘制轨迹
figure(3);
set(0,'defaultfigurecolor','w')
plot(X(1,:), X(2,:), 'r.-', Z(1,:), Z(2,:), 'g.-', PCenter(1,:), PCenter(2,:), 'b.-');
axis([0 100 0 100]);
set(gca,'XTick',0:10:100) %改变x轴坐标间隔显示 这里间隔为10
set(gca,'YTick',0:10:100) %改变y轴坐标间隔显示 这里间隔为10
legend('真实轨迹', '测量轨迹', '粒子群几何中心轨迹');
xlabel('横坐标 x'); ylabel('纵坐标 y');
%% 绘制误差
figure(4);
set(0,'defaultfigurecolor','w')
%set(gca,'FontSize',12);%设置图标字体大小
plot(err(1,:),'b.-');%err1为各时刻 真实位置与粒子群中心的几何距离
hold on
plot(err(2,:),'r.-');%err2为各时刻 真实位置与测量位置的几何距离
hold off
xlabel('步数 t');
legend('粒子群误差', '测量误差');
title('真实位置与粒子群中心的集合距离');

3 更多

3.1 失效恢复问题

蒙特卡罗定位以目前的形式能够解决全局定位问题，但是不能从机器人绑架中或全局定位失效中恢复。定位过程中，获取位置的同时，不在最可能位置处的粒子会逐渐消失，在某个时候，只有单一位置的粒子能够“幸存”，如果这个位姿碰巧是错误的，算法不能恢复。实际上，任何随机算法（如蒙特卡罗定位算法），在重采样步骤中可能意外地丢弃所有正确位置附近的粒子，特别是当粒子数较少，且粒子扩散到较大空间时，这个问题就显得很重要了。

• 解决办法：
  通过简单的探索算法可以解决这个问题，探索算法的思想是：增加随机粒子到粒子集合。通过假设机器人可能以小概率遭到绑架，注入一些随机粒子，从而在运动模型上产生一些随机状态，即使机器人不被绑架，随机粒子也能提升额外的鲁棒性级别。

• 这引起两个问题：
  (1)在每次算法迭代中，应该增加多少粒子；(2)从哪种分布产生这些粒子。

• 解答：
  (1)一种简单的方法是每次迭代增加固定数目的随机粒子；另一种更好的想法是基于某些定位性能的评估增加粒子。其中，实现第二种想法的一个方法是监控传感器测量的概率分布，在粒子滤波里，重要性权重是这个概率分布的随机估计，其均值(即增加的粒子数目)为：
  

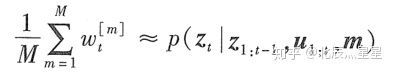
(2)一种简单的方法是根据均匀分布在位置空间产生粒子，并用当前观测值加权这些粒子；另一种更好的想法是根据测量分布直接产生粒子，根据观测似然分布，附加的粒子能够直接放置在相应的位置上。