1. OpenGL简介
OpenGL是Open Graphics Library的缩写[2],是个定义了一个跨编程语言、跨平台的编程接口的标准,显卡通常有OpenGL的实现,不同显卡上的OpenGL实现也不一定相同,OpenGL标准不是平台相关的,所以同一个程序可能在不同的显卡上运行。OpenGL API只处理图形渲染,并不提供动画、定时器、文件IO、图像文件格式处理、GUI等功能,GLUT[5]并不是OpenGL,也不是OpenGL的一部分,它仅是被一些用户用于创建OpenGL窗口。OpenGL不是开源代码,OpenGL指的是开放标准,在网上[4]可以找到,任何人都可以免费下载,也有一个开源的GL实现,名叫 Mesa3D,已经实现了OpenGL 3.0和GLSL 1.30。
OpenGL被当作客户端-服务器系统来实现的,应用程序是客户端,图形硬件厂商提供的OpenGL实现是服务器。如图1所示,客户端程序需要调用OpenGL的接口实现3D渲染,那么OpenGL命令和数据会缓存在RAM中,在一定条件下,会将这些命令和数据通过CPU时钟发送到VRAM,在GPU的控制下,使用VRAM中的数据和命令,完成图形的渲染,并将结果存入帧缓冲区中,帧缓冲区中的帧最终会被发送到显示器上,显示出结果。在现代的图形硬件系统中,还支持不通过CPU时钟直接将数据由RAM发送至VRAM或直接将数据由帧缓冲区发送至RAM(例如OpenGL中的VBO,PBO)。
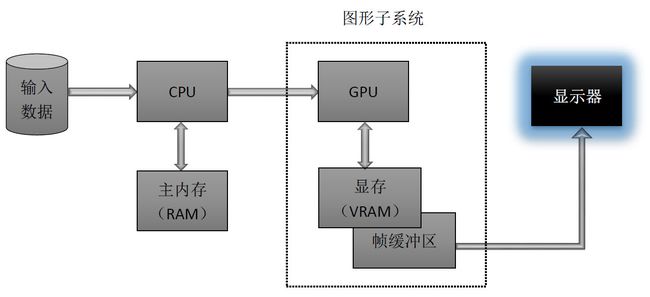
图1. 计算机图形硬件系统[6]
在一些OpenGL实现中,比如那些与X windows system相关的实现,客户端和服务器在不同的机器上执行,两者通过网络连通起来。在这种情况下,客户端发送OpenGL命令,这些命令被转化成窗口系统相关的协议,再通过共享的网络发送给server。
如图2所示,OpenGL中的顶点、像素等数据需要通过不同阶段的处理,才能产生最后的可视图像,就像是工厂里的生产线,称为图形渲染管线。像素和顶点数据可以选择存储在显示列表中,我们可以把显示列表看成是存储数据的媒介,用于加速渲染速度。顶点数据经过求值器,产生法向量、纹理坐标、点的空间坐标等,通过顶点操作和图元装配,生成相应的像素信息,进行光栅化处理,光栅化是把几何和像素数据转化成片段,每个片段块对应帧缓冲区中的一个像素。其中,顶点操作和图元装配中又可以细分出一条渲染管线,这里称为顶点处理管线。在光栅化完成后,还可以根据命令,对每个像素进行处理,最后写入帧缓冲区内。
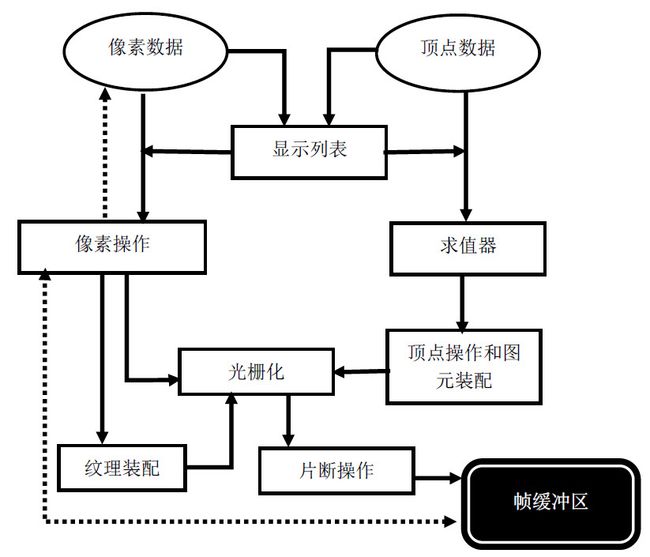
图2. OpenGL的图形渲染管线[1]
2. 顶点处理管线
本节介绍如何将三维空间上的图元转化为二维屏幕上渲染出的图元,包括图元的顶点位置、大小等。
顶点的处理管线如图2所示,设我们在三维空间上的坐标(0,0,0)处画一个小球,对小球移动至(1,0,0),再绕着y坐标轴旋转90度,对小球位移和旋转的处理完成后,这是模型矩阵完成的功能。在空间中放置好模型后,需要架设摄像机,然后才能够观察到模型,架设摄像机,是视图矩阵实现的功能,把这两部分统一起来,就得到模型视图矩阵。接着,需要把小球投影到一个虚拟屏幕上,计算小球的虚拟投影点,这是投影矩阵完成的功能。如果场景中存在多个小球,相对于摄像机的视角,有一部分小球被前面的小球阻挡了,那么被阻挡的小球就不会被渲染出来,裁剪掉被阻挡的模型就是裁剪处理完成的功能。最后,根据屏幕的长宽,把虚拟屏幕映射到真实屏幕上。这就是OpenGL顶点处理的简化流程。接着,详细阐述技术细节。
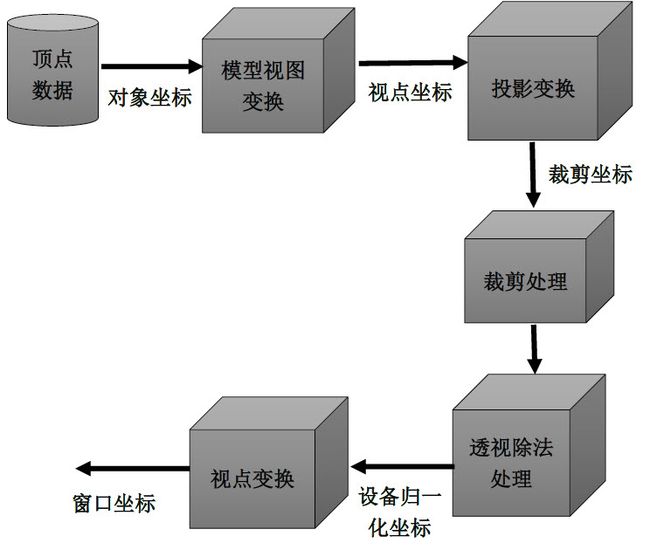
图3. 顶点处理管线[7]
首先引入齐次坐标的概念,齐次表示是什么?为什么要采用齐次表示呢?在 维空间上,把点和向量扩展一维,就是它们的齐次表示,点P的齐次表示为(p1,p2,⋯,pn,1),向量v⃗ 的齐次表示为(v1,v2,⋯,vn,0)。一个顶点可以表示为(x,y,z,1),一个向量则表示为(a,b,c,0)。点表示空间上的一个位置,向量表示一个方向而没有具体的位置,因此点的位移是有意义的,但是向量的位移是没有意义的。采用齐次表示,三维空间上的图形变换包括旋转、位移、透视、正交等都可以用一个4×4的矩阵来表示,矩阵的连乘就是各个矩阵代表的变换的叠加。因此,图3中的模型视图变换、投影变换都可以用一个4×4的矩阵来表示。
2.1. 模型视图变换
我们又可以把模型视图矩阵细分为两个部分,如图4所示,对象坐标先经过模型变换,转化为世界坐标,再经过视图变换,转化为视点坐标。
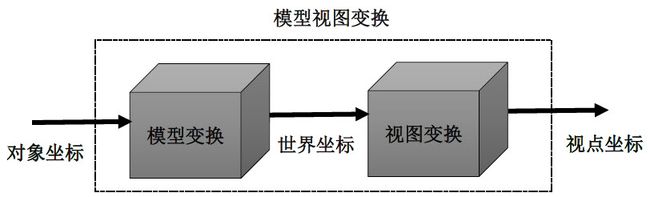
图4. 模型视图变换
模型变换,只涉及仿射变换(互相平行的两条直线,经过变换后仍然能保持平行),这里介绍其中的3个变换:位移、旋转和缩放。三维空间上的,位移用矩阵T表示,则(x,y,z,1)⋅T=(x+a,y+b,z+c,1),相当于把齐次坐标(x,y,z,1)移动(a,b,c)的偏移量。
T=⎛⎝⎜⎜⎜100a010b001c0001⎞⎠⎟⎟⎟ (1)
在三维空间上,绕着x轴、y轴、z轴的旋转4×4的矩阵Rx(θ),Ry(θ),Rz(θ)表示,有:
Rx(θ)=⎛⎝⎜⎜⎜10000cosθ−sinθ00sinθcosθ00001⎞⎠⎟⎟⎟,Ry(θ)=⎛⎝⎜⎜⎜cosθ0sinθ00100−sinθ0cosθ00001⎞⎠⎟⎟⎟,Rz(θ)=⎛⎝⎜⎜⎜cosθ−sinθ00sinθcosθ0000100001⎞⎠⎟⎟⎟(2)
其中,沿着轴相反的方向观察,θ表示逆时针旋转的角度。
在三维空间上,对模型的缩放变换的矩阵用S表示,分别将坐标x轴、y轴、z轴上的分量分别缩放至原先的a,b,c倍。
S=⎛⎝⎜⎜⎜a0000b0000c00001⎞⎠⎟⎟⎟ (3)
这3个变换对应OpenGL中的三个接口为:glTranslate*(),glRotate*(),glScale*()。
接着,讨论视图变换,就相当于是架设摄像机的问题。如图5所示,架设摄像机,相当于定义摄像机的位置eye,摄像机垂直向上的方向up−→,和摄像机观察点look。那么,可以得到n→=eye−look,u→=up−→×n→,v→=n→×u→,推导出的视图矩阵Mview为:
Mview=⎛⎝⎜⎜⎜⎜uxuyuz−eye⋅u→vxvyvz−eye⋅v→nxnynz−eye⋅n→0001⎞⎠⎟⎟⎟⎟ (4)

图5. 架设摄像机
对于任意一个世界坐标V经过视图变换后,会得到相对于摄像机坐标系统下的坐标V′,即V′=V⋅Mview,称为视点坐标。例如世界坐标系下的坐标eye,向量u→,v→,n→经过视图变换后得到:
(eyex,eyey,eyez,1)⋅Mview=(0,0,0,1)
(ux,uy,uz,0)⋅Mview=(1,0,0,0) (5)
(vx,vy,vz,0)⋅Mview=(0,1,0,0)
(nx,ny,nz,0)⋅Mview=(0,0,1,0)
相反,如果要将一个视点坐标变换到世界坐标,相当于是视图变换的逆过程,即V=V′⋅M−1view,其中:
M−1view=⎛⎝⎜⎜⎜⎜uxvxnxeyexuyvynyeyeyuzvznzeyez0001⎞⎠⎟⎟⎟⎟ (6)
在OpenGL中,模型变换和视图变换统一为模型视图变换。用函数glMatrixMode()来指定变换类型,如果是模型视图变换,则选用参数GL_MODELVIEW。如下面的代码片段所示:
| 1 2 3 |
glMatrixMode(GL_MODELVIEW); //规定当前处理的矩阵是模型视图矩阵栈
glLoadIdentity(); //把模型视图矩阵设置为单位矩阵
drawSphere();
|
此时,摄像机放置在默认位置,即放置在原点,up=(0,1,0),向z轴的负方向观察,如图6所示。
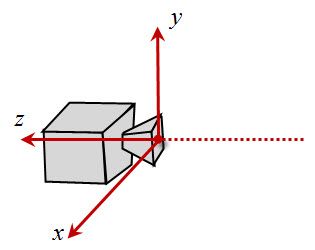
图6. 默认情况下,摄像机的架设
不采用默认的摄像机架设,OpenGL中提供了API接口gluLookAt()用于架设摄像机,接口的定义如下所示,(eyex, eyey, eyez)规定摄像机的位置,(centerx, centery, centerz)规定观察点,即上面提到的look坐标,(upx, upy, upz)规定摄像机的垂直朝向。
| 1 |
void gluLookAt( GLdouble eyex, GLdouble eyey, GLdouble eyez, GLdouble centerx, GLdouble,centery, GLdouble centerz, GLdouble upx, GLdouble upy, GLdouble upz )
|
当采用多个变换时,需要特别注意变换的顺序,如下面的代码片段所示:
| 1 2 3 4 |
//先将对象进行位移(a, b, c)的操作,再将对象绕(1,0,0)轴旋转angle度。
glRotatef(angle, 1, 0, 0);
glTranslatef(a, b, c);
drawObject();
|
此外,OpenGL还提供了一些其它的矩阵变换函数,包括如下所示:
| 1 2 3 4 5 6 |
glLoadIdentity()
glLoadMatrix{fd}(m)
glLoadTransposeMatrix{fd}(m)
glMultMatrix{fd}(m)
glMultTransposeMatrix{fd}(m)
glGetFloatv(GL_MODELVIEW_MATRIX, m)
|
2.2. 投影变换
投影变换包括透视投影、正交投影、斜投影等,但本节只阐述其中的透视投影。如图7所示,原点表示摄像机的位置,由它引出一个金字塔形的视锥,近的切一刀,就称为近平面,远的切一刀,就称为远平面。投影变换做的就是将三维空间上的点投影到近平面上。
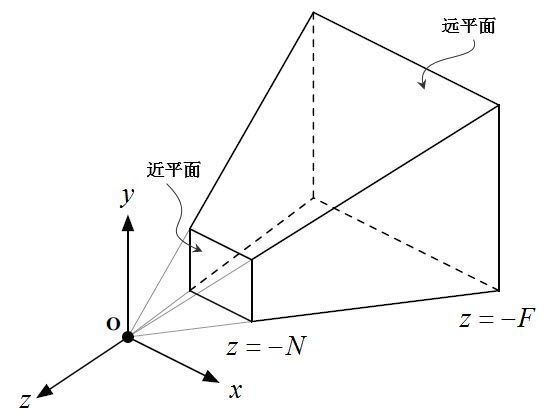
图7. 透视投影
我们先考虑最简单的点的透视投影,如图8所示,将一个点(Px,Py,Pz)投影到摄像机的平面上,在平面上的坐标为(x∗,y∗),平面与原点之间的距离为N。易知x∗Px=N−Pz,其中Pz是一个负数,则可以推导出x∗=N⋅Px−Pz,同理,可以得到y∗=N⋅Py−Pz,那么点(Px,Py,Pz)在平面上的投影点为
(x∗,y∗)=(N⋅Px−Pz,N⋅Py−Pz) (7)

图8. 点的透视
由于透视变换不是仿射变换,即互相平行的两条直线经过投影变换后,就不再是互相平行的,如图9所示,互相不行平的两条铁却相交于一点。真实世界观察到的物体均是透视视角,这世上或许不存在偶然,就好像一切都是必然的,平行的世界能相遇应该说是一种缘分也好。从图形学的原理来讲,通过透视变换,互相平行的两条直线(非平行于屏幕)最终必然会相交于一个点,我们称这个点为“灭点”,接下来阐述下其原理。

图9. 平行的铁轨在遥远的前方相交于同一个点
假设一条直线通过点A=(Ax,Ay,Az),方向向量为c→=(cx,cy,cz),直线用参数形式可以表示为P(t)=A+c→⋅t,代入等式(7),可以得到:
P(t)=(NAx+cxt−Az−czt,NAy+cyt−Az−czt)(8)
由等式(8)可以看出,如果cz=0,即直线平行于屏幕,则两条互相平行的直线始终能保持平行状态;如果cz≠0,令t→∞,则有p(∞)=(Ncx−cz,Ncy−cz),即灭点只与直线的方向向量有关。
前面阐述了将三维空间上的点投影到屏幕上,得到的在屏幕上的坐标点,但是我们发现这里存在一个问题,就是如果三维空间上多个点都投影到屏幕上相同的一个点,由于我们前面的计算摒弃了深度值,因此,我们无法确定是保留哪个点,即无法完成隐藏面的移除,所以引入伪深度(pseudodepth)的概念。点的投影公式(7)可以变换为:
(x∗,y∗,z∗)=(N⋅Px−Pz,N⋅Py−Pz,aPz+b−Pz)(9)
其中,a=−F+NF−N,b=−2FNF−N,F,N参见前面的。
这里,我们可以画出伪深度z∗与−Pz的函数曲线,如图10所示。当−Pz=N时,z∗=−1;当−Pz=F时,z∗=1。显然,对于伪深度值z∗≺−1的点,在比近平面更近的位置;对于伪深度值z∗≻1的点,比远平面更远的位置,这就为后面的裁剪提供了非常大的便利。
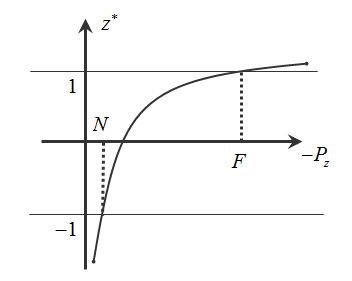
图10. 伪深度z∗与−Pz的函数曲线
现在考虑透视变换的矩阵表示M1:
M1=⎛⎝⎜⎜⎜⎜⎜N0000N0000−F+NF−N−2FNF−N00−10⎞⎠⎟⎟⎟⎟⎟(10)
因为近平面的长宽也是有限的,无法将位于近平面后面的所有物体都投影到屏幕上,用四个参数来规定近平面,如图11所示。显然,近平面确定了,与之相对应的远平面也确定了。
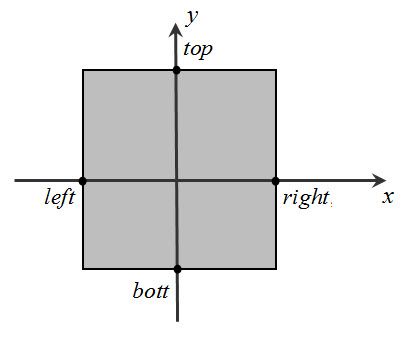
图11. 近平面
接着,此时,在近平面上的投影坐标是介于[left,right]和[bott,top]之间的数值,再把投影坐标值进行缩放操作,使得投影坐标的x∗,y∗均介于[−1,1],缩放变换矩阵用M2表示:
M2=⎛⎝⎜⎜⎜⎜⎜⎜2right−left00−right+leftright−left02top−bottom0−top+bottomtop−bottom00100001⎞⎠⎟⎟⎟⎟⎟⎟ (11)
那么透视变换用矩阵Mperspective表示为:
Mperspective=M1M2=⎛⎝⎜⎜⎜⎜⎜⎜⎜2Nright−left0right+leftright−left002Ntop−botttop+botttop−bott000−(F+N)F−N−2FNF−N00−10⎞⎠⎟⎟⎟⎟⎟⎟⎟(12)
任何一个坐标(x,y,z)经过透视变换,得到(x∗,y∗,z∗)=(x,y,z)⋅Mperspective。显然,如图7所示,如果该坐标点处于视锥内且位于近平面和远平面之间的坐标,则变换后,x∗,y∗,z∗均是介于[−1,1]之间的值,即不在范围内的点均会被裁剪掉,大大简化了后面的裁剪步骤。
OpenGL中,也提供了两个重要的接口,用于设置透视变换的参数,glFrustum()和gluPerspective(),分别如下所示:
| 1 2 |
void glFrustum( GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near,GLdouble far )
void gluPerspective( GLdouble fovy, GLdouble aspect, GLdouble zNear, GLdouble zFar )
|
接口glFrustum()指定的参数与矩阵(12)中变量的对应关系非常的直观,不再赘述,特别说明下接口gluPerspective()与矩阵(12)中变量的对应。如图12所示,左图是一个透视视锥,右图是该视锥在Y−Z平面上的截面图,函数变量fovy对应图中的角度θ,则有:
top=N⋅tan(π180⋅θ2)bott=−top (13)
函数变量aspect定义了长宽的比例系数,则有:
right=top⋅aspectleft=−right (14)

图12. gluPerspective接口说明
与模型视图矩阵类似,需要采用函数glMatrixMode()指定矩阵栈类型,投影变换的参数选择为GL_PROJECTION,简单的示例代码片段如下所示:
| 1 2 3 |
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45, width / height, 1.0f, 100.0f); //width和height分别表示显示窗口的宽和长
|
2.3. 裁剪、透视除法、视点变换
裁剪发生在投影变换之后,如果一个点在视锥内且位于近平面和远平面之间,那么变换后,该点的坐标值x∗,y∗,z∗均是介于[−1,1]之间的值,如图13所示,称该正方体区域为正规化可视空间,简称为CCV(Canonical View Volume)。在实际绘图的时候,不可能只是一个点一个点的指定,还可能是绘制一条直线、一个三角、一个多边形等等,裁剪阶段要做的是保留CCV内的图元,并且裁剪掉CCV外的图元。图元的基础是直线,比较经典的直线裁剪算法有Byrus裁剪法[8],Liang-Barsky裁剪法[9,10],快速裁剪算法(简称为SPY算法)[11],Nicholl-Lee-Nicholl算法(简称为NLN算法)[12],在Hill& Kelley[7]第7.4.4节也有裁剪算法的介绍,这里不重点介绍。
由于至此,我们一直采用的是齐次坐标。接着,通过透视除法,即齐次坐标的前三个分量除以第四个分量,再丢弃第四个分量,得到一个三元组新坐标,称此时得到的坐标为规一化设备坐标。注意,规一化设备坐标中的每个分量都介于[−1,1]之间,因此才有了视点变换。
设备归一化坐标通过缩放和位移,使它适合渲染窗口的渲染,这就是视点变换阶段要做的工作。以OpenGL中视点变换的接口函数glViewport()来解释其背后的原理,接口申明如下所示:
| 1 |
void glViewport( GLint x, GLint y, GLsizei width, GLsizei height )
|
x, y规定视窗的左下角坐标 ,width, height规定视窗的宽和高度,那么规一化设备坐标与窗口坐标的线性对应关系有:
{−1→x1→x+w{−1→y1→y+h{−1→n1→f (15)
规一化设备坐标与窗口坐标的变换等式有):
⎛⎝⎜xwywz⎞⎠⎟=⎛⎝⎜⎜⎜w2xndc+(x+w2)h2yndc+(y+h2)f−n2zndc+f+n2⎞⎠⎟⎟⎟ (16)
其中,(xw,yw)表示窗口坐标,(xndc,yndc,zndc)表示规一化设备坐标。
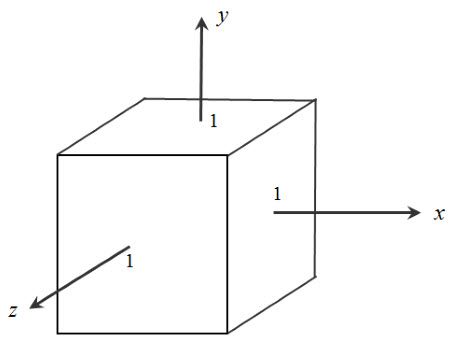
图13. 正规化可视空间CCV
在完成了视点变换后,就会利用窗口坐标进行光栅化处理。
2.4. 代码示例
采用GLUT库,实现一个非常简单的DEMO,如下所示:

图14. 简单的金字塔形渲染
| /************************************************************************
\link www.twinklingstar.cn
\author Twinkling Star
\date 2015/02/03
\file opengl_helloworld.cpp
****************************************************************************/
#include
void init()
{
glClearColor(0.0f,0.0f,0.0f,0.0f);
glClear(GL_COLOR_BUFFER_BIT);
}
void draw(void)
{
//set the modelview matrix stack. GL_MODELVIEW
glMatrixMode(GL_MODELVIEW);
glClear(GL_COLOR_BUFFER_BIT );
glLoadIdentity();
glTranslatef(0.0f,0.0f,-6.0f);
glBegin(GL_TRIANGLES); // Start Drawing A Triangle
glColor3f(1.0f,0.0f,0.0f); // Red
glVertex3f( 0.0f, 1.0f, 0.0f); // Top Of Triangle (Front)
glColor3f(0.0f,1.0f,0.0f); // Green
glVertex3f(-1.0f,-1.0f, 1.0f); // Left Of Triangle (Front)
glColor3f(0.0f,0.0f,1.0f); // Blue
glVertex3f( 1.0f,-1.0f, 1.0f); // Right Of Triangle (Front)
glColor3f(1.0f,0.0f,0.0f); // Red
glVertex3f( 0.0f, 1.0f, 0.0f); // Top Of Triangle (Right)
glColor3f(0.0f,0.0f,1.0f); // Blue
glVertex3f( 1.0f,-1.0f, 1.0f); // Left Of Triangle (Right)
glColor3f(0.0f,1.0f,0.0f); // Green
glVertex3f( 1.0f,-1.0f, -1.0f); // Right Of Triangle (Right)
glColor3f(1.0f,0.0f,0.0f); // Red
glVertex3f( 0.0f, 1.0f, 0.0f); // Top Of Triangle (Back)
glColor3f(0.0f,1.0f,0.0f); // Green
glVertex3f( 1.0f,-1.0f, -1.0f); // Left Of Triangle (Back)
glColor3f(0.0f,0.0f,1.0f); // Blue
glVertex3f(-1.0f,-1.0f, -1.0f); // Right Of Triangle (Back)
glColor3f(1.0f,0.0f,0.0f); // Red
glVertex3f( 0.0f, 1.0f, 0.0f); // Top Of Triangle (Left)
glColor3f(0.0f,0.0f,1.0f); // Blue
glVertex3f(-1.0f,-1.0f,-1.0f); // Left Of Triangle (Left)
glColor3f(0.0f,1.0f,0.0f); // Green
glVertex3f(-1.0f,-1.0f, 1.0f); // Right Of Triangle (Left)
glEnd(); // Done Drawing The Pyramid
glFlush();
}
void reshape(GLsizei w,GLsizei h)
{
//set viewport
glViewport(0,0,w,h);
//Set the projection stack, GL_PROJECTION
glMatrixMode(GL_PROJECTION);
//set the unit matrix.
glLoadIdentity();
gluPerspective(45, w / h, 1.0f, 100.0f);
}
int main(int argc,char ** argv)
{
glutInit(&argc,argv);
glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);
glutInitWindowSize(400,400);
glutCreateWindow("example");
init();
glutReshapeFunc(reshape);
glutDisplayFunc(draw);
glutMainLoop();
return(0);
}
|
3.纹理
本节将介绍纹理映射的原理,图形硬件中的处理和基本的纹理对象的使用方法。
3.1. 纹理插值
给对象的表面增加各种纹理,可以使场景更加的形象生动,图15所示,就显示了给场景中增加纹理的情况。

图15. 纹理映射
对象表面的纹理可以理解为覆盖在对象表面的图像,图像是由一个个的像素构成的二维数组。像这样存储有图像数据的二维数组可以通过两种方式生成:(1)位图纹理(Bitmap Texture),通过电脑的数字照片、图片等生成二维的数组数据;(2)过程纹理(Procedural texture),通过数学公式来生成一个二维的数组数据。如图16所示,左边的纹理是由一个照片得到的,右边的纹理是由程序依据一个数学模型计算出来的。像这样一个二维的数组可以称之为纹理,纹理上的像素点都有一个坐标,称之为纹理坐标,与纹理有关的坐标轴常用的字母是s和t,水平方向指的是s方向,垂直方向指的是t,s和t限制在[0,1]范围以内。

图16. 左边是位图纹理,右边是过程纹理
将纹理坐标与顶点坐标对应的程序也较简单,将图15中左图纹理映射到一个正方形表面上,采用的代码片段如下所示。纹理坐标(0.0f, 0.0f)对应顶点坐标(1.0f, 2.5f , 1.5f),纹理坐标(0.0f, 1.0f)对应顶点坐标(1.0f, 3.7f, 1.5f),依次类推,将整个纹理映射到三维空间中。
| 1 2 3 4 5 6 |
glBegin(GL_QUADS);
glTexCoord2f(0.0f , 0.0f); glVertex3f(1.0f , 2.5f , 1.5f);
glTexCoord2f(0.0f , 1.0f); glVertex3f(1.0f , 3.7f , 1.5f);
glTexCoord2f(1.0f , 1.0f); glVertex3f(2.0f , 3.7f , 1.5f);
glTexCoord2f(1.0f , 0.0f); glVertex3f(2.0f , 2.5f , 1.5f);
glEnd();
|
显然,上面的纹理映射只指定了四边形的四个顶点,四边形内部的纹理坐标是怎么计算的呢?接下来,我们来阐述下其背后的数学原理。
很容易想到的方法,就是线性插值,例如指定世界坐标(10.0f, 10.0f)是纹理空间坐标(0.0f, 0.0f)的颜色值,指定世界坐标(20.0f, 20.0f)是纹理空间坐标(1.0f, 1.0f)的颜色值,那么世界坐标(15.0f, 15.0f)的对应的纹理空间的坐标,按照线性插值的理论,就应该是对应纹理空间(0.5f, 0.5f)的颜色值。然而,线性插值在纹理空间的映射上是否是正确的呢?答案是不正确的。纹理映射是发生在透视变换之后,如图17上图所示,由于已经经过透视变换,近大远小的原理,单位距离,在靠近眼睛处会显得比较大,但远离眼睛处会显得很小。如果采用等距采样,即前面讲的线性插值的话,那么出错是必然的,如图18所示。

图17. 线性插值的采样

图18. 线性插值和透视修正的插值

图19. 插值的映射
接着,我们阐述正确的插值算法。如图10所示,直线AB通过矩阵M,变换成直线ab,A映射到a,B映射到b,AB之间的R(g)=lerp(A,B,g)映射到r(f)=lerp(a,b,f)点,其中lerp(A,B,g)=A+(B−A)g。计算g与f的关系,推导如下所示:

推导出g与f的关系,与b4/a4比值有关。为什么可能存在b4/a4比值不为1的情况呢?因为,OpenGL中采用到了齐次坐标,当进行透视变换的时候,就可能导致b4/a4比值不为1。如果变换M是仿射变换,则g与f相同;如果是透视变换,则可能会不同。
把g与f的关系等式代入R(g)=A(1−g)+B,则得到等式(17),Blinn[13]称该技术为双曲线插值(Hyperbolic Interpolation)。这里还有一个问题,为什么采用g=Function(f)的形式,而不是采用f=Function(g)的形式呢?这个问题可以这样子理解,矩阵变换(特别是透视变换)前的纹理计算可以通过简单的线性插值得到,但是通过透视变换后,根据这时候的比值f,来反推出透视变换前与这个比值对应的g,而求g值的纹理坐标只需要线性插值即可完成。
R(g)=lerp(Aa4,Bb4,f)lerp(1a4,1b4,f) (17)
前面介绍了线段AB¯¯¯¯¯¯¯¯映射到线段ab¯¯¯¯¯上时,线段ab¯¯¯¯¯上的点的纹理坐标的计算。但对于一个面来说,其插值又是怎么进行的呢?如图20所示,左侧的四边形经过矩阵变换M后,得到右侧的四边形。设点A1,B1的齐次坐标分别是(a1,a2,a3,a4),(b1,b2,b3,b4),它们对应的纹理坐标分别是(sA1,tA1),(sB1,tB1)。考虑右侧的四边形的纹理坐标的计算,在扫描线y上,对于点p1来说,即线段a1b1¯¯¯¯¯¯¯¯¯间的插值,有y=lerp(ybott,ytop,f),即f=(y−ybott)/(ytop−ybott),根据等式(18)容易计算出点p1的纹理坐标为:
(sp1,tp1)=⎛⎝lerp(sA1a4,sB1b4,f)lerp(1a4,1b4,f),lerp(tA1a4,tB1b4,f)lerp(1a4,1b4,f)⎞⎠(18)
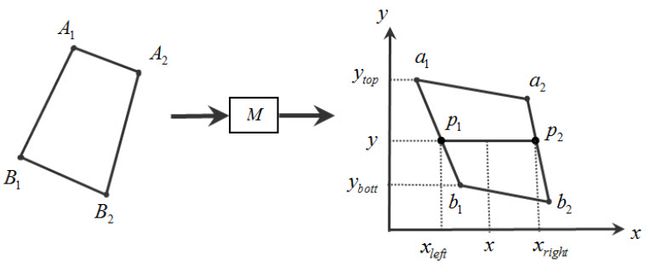
图20. 面的纹理插值
同理,可以计算出点p2的纹理坐标为(sp2,tp2),在得到坐标p1,p2的纹理坐标后,还可以计算出p1,p2对应的齐次坐标。再次利用双曲线插值,可以得到线段p1p2¯¯¯¯¯¯¯¯¯之间的纹理值。
3.2. 纹理的使用
不管是位图纹理还是过程纹理,初始阶段一定是存储在主内存中,再通过调用glTexImage2D()或者gluBuild2DMipmaps()接进行拆分,即根据像素的存储模式和像素转换操作,将纹理数据发送到显存上,然后才能通过GPU进行纹理的渲染,如图21所示。

图21. 纹理数据的存储
接着,讨论在OpenGL中如何使用纹理,主要有以下几个步骤:
3.2.1. 启动纹理
本节只讨论二维纹理,在应用二维纹理时,需要激活它,默认情况下是未激活的。
| 1 |
glEnable(GL_TEXTURE_2D);
|
3.2.2. 生成纹理名字
首先,必需为每个纹理对象分配一个编号,即是这个纹理对象的名字,使我们在使用的时候,清楚用的是哪个纹理对象,接口glGenTextures()干得就是这个活。
| 1 |
void glGenTextures(Glsizei n,GLuint* textures);
|
当然,我们也可以很任性,不使用由它分配的名字,我们自己指定一个名字,将自己指定的名字绑定一个纹理对象,这种任性是允许的。但是,我们可能会付出一定的代价,就是我们指定的名字,可能已经被使用了。此时,我们又提供了另外一个接口glIsTexture()来避免我们的任性造成的悲剧,如果textureName是一个被绑定过的纹理名字且未被删除,则返回GL_TRUE。
| 1 |
GLboolean glIsTexture(Gluint textureName);
|
3.2.3. 创建并使用纹理对象
在给纹理对象起好名字了,但是这个时候,还并没有创建纹理对象,就像生孩子,只给孩子起了名字,但是孩子还没有生出来。接着,需要调用接口glBindTexture():
| 1 |
void glBindTexture(GLenum target,GLuint texture); //这一小节,target的值都是GL_TEXTURE_2D,表示一个二维纹理图片
|
这个接口有三个功能:
(1) texture非0且是第1次作为该函数的参数,用于创建一个新的纹理对象并给它分配名字;
(2) 名字是texture的纹理对象已经绑定完成,调用这个函数实现的功能是激活该纹理对象;
(3) 如果texture是0,OpenGL停止使用纹理对象且返回一个未被命名的默认纹理。
3.2.4. 存储纹理数据
在给纹理对象起好了名字,创建了纹理对象并将它与名字绑定好了后,纹理对象还不存在具体的数据。再以生孩子为例,至此,已经有了孩子,这个孩子叫“陈旭元”,但是他还不能写程序,我们需要教他C、C++、汇编等等,他才能写出能看的code。接口glTexImage2D()或gluBuild2DMipmaps()就是将纹理数据,由主内存,经过拆分处理,发送到显存,将它与我们指定的纹理对象绑定。这两个函数接口的申明如下所示:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
void glTexImage2D( Glenum target,
Glint level,
GLint internalFormat,
GLsizei width,
GLsizei height,
GLint border,
GLenum format,
GLenum type,
const GLvoid * data);
// target规定目标纹理,必需是以下的任意一个: GL_TEXTURE_2D,GL_PROXY_TEXTURE_2D等
// level规定细节层次数(level of detail),0表示基本的图像级别
// internalFormat规定纹理图像存储在硬件内存中的格式,必需是1,2,3,4,或者是下面的某个参数:GL_ALPHA, GL_ALPHA4, GL_ALPHA8等
// width与height规定了纹理图像的宽和高,如果有边界的话就包括边界,它的宽度和高度必需符合公式2n+2b,b表示border的宽度,至少是64*64的尺寸。
// border规定了边界宽度,必需是0或者1。
// format规定了像素数据data的格式,可以被正确接收的类型如下所示:GL_RGB, GL_BGR,GL_RGBA, GL_BGRA,GL_COLOR_INDEX等
// type规定了像素数据data的类型,包括以下几种格式:GL_UNSIGNED_BYTE, GL_BYTE, GL_BITMAP, GL_UNSIGNED_SHORT, GL_SHORT, GL_UNSIGNED_INT, GL_INT, and GL_FLOAT。
// data是一个指向内存中图像数据的指针
GLint gluBuild2DMipmaps( GLenum target,
GLint internalFormat,
GLsizei width,
GLsizei height,
GLenum format,
GLenum type,
const void * data);
// target规定目标纹理,必需是GL_TEXTURE_2D
// internalFormat规定纹理图像存储在硬件内存中的格式,必需是1,2,3,4
// width与height规定了图像的宽和高
// format规定了像素数据的格式,可以被正确接收的类型如下所示:GL_COLOR_INDEX, GL_RED, GL_GREEN, GL_BLUE, GL_ALPHA, GL_RGB, GL_RGBA, GL_BGR_EXT, GL_BGRA_EXT, GL_LUMINANCE, or GL_LUMINANCE_ALPHA
// type规定了像素数据data的类型,包括以下几种格式:GL_UNSIGNED_BYTE, GL_BYTE, GL_BITMAP, GL_UNSIGNED_SHORT, GL_SHORT, GL_UNSIGNED_INT, GL_INT, or GL_FLOAT。
// data是一个指向内存中图像数据的指针
|
存储纹理数据的调用示例如下所示:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
glTexImage2D(GL_TEXTURE_2D, //当前处理的是二维纹理
0, //纹理细节层号,这里设置为0
3, //规定存储到纹理对象中颜色分量,即规定像素数据在纹理对象中的存储格式
width, height, //纹理图片的宽和高
0, //纹理的边界,这里设置成0
GL_RGB, //存储在像素数据data中的颜色数据是以R,G,B的形式保存的
GL_UNSIGNED_BYTE, //在像素数据中,每一种颜色分量以无符号字节的格式存储
data //指向像素数据的指针
);
gluBuild2DMipmaps(GL_TEXTURE_2D, //当前处理的是二维纹理
3, //规定存储到纹理对象中颜色分量,即规定像素
width, height, //纹理图片的宽和高
GL_RGB, //存储在像素数据data中的颜色数据是以R,G,B的形式保存的
GL_UNSIGNED_BYTE, //在像素数据中,每一种颜色分量以无符号字节的格式存储
data //指向像素数据的指针
);
|
对比这两个函数的不同点:
(1)glTexImage2D()函数对纹理图像的尺寸有要求,它的宽度和高度必需符合公式2n+2b,b表示border的宽度;gluBuild2DMipmaps()函数没有尺寸的限制,可以是任意分辨率的图像,但这个函数不稳定,传入某些纹理图像时可能会发生异常。
(2)glTexImage2D()调用一次,只能指定一个纹理层数;gluBuild2DMipmaps()函数可以自动生成所有的纹理细节层,但是可能存在的问题就是自动生成的纹理细节层存在错误,使用得渲染出的界面效果很怪异。
所谓的纹理多重细节层(Mipmap),最早是由Williams(1983)[14]提出的。当纹理图片映射到一个更小的物体上时,如果物体发生了移动,就会产生闪烁或者抖动现象,而使用mipmap就可以解决这个问题。如果贴图的基本尺寸是64x16像素的话,它mipmap就会有6个层级,依次层级大小就是:32x8,16x4,8x2,4x1,2x1,1x1(一个像素)。较小的纹理图像通常是原始图像过滤的版本,是对原始图像进行适当匀缩的结果,每个层级是上一层级的四分之一的大小。OpenGL没有规定使用特定的方法来计算低分辨率的纹理图像,因此不同大小的纹理也可以是完全不相关的。
哪个mipmap层将作为一个特定多边形的纹理取决于纹理图像的大小和被贴图多边形的大小之间的缩放因子,这个缩放因子称为ρ,另外再定义一个λ值,则有
λ=log2ρ+lodbias
其中,纹理图像是多维的,则ρ各维中最大的缩放因子,其中lodbias表示偏移细节层,它是由glTexEnv*()函数设置的一个常量值,默认值是0。
3.2.5. 设置过滤方法
当纹理发生放大或者缩小时,可以使用glTexParameter*()函数设置过滤方法。
| 1 2 |
void glTexParameter{if}( GLenum target,GLenum pname,TYPE param);
void glTexParameter{if}v( GLenum target, GLenum pname,TYPE* params);
|
target规定目标纹理,可取的常量为:GL_TEXTURE_1D,GL_TEXTURE_2D,GL_TEXTURE_3D。
不同的pname和param表示的功能如下表所示:

3.2.6. 指定纹理坐标
将纹理坐标与顶点坐标绑定,主要用到的接口是glTexCoord()。
| 1 2 |
void glTexCoord{1234}{sifd}(TYPE coords);
void glTexCoord{1234}{sifd}v(const TYPE* coords);
|
以二维纹理图片为例,举个简单的例子,画一个四边形,并且将纹理坐标映射到这个四边形上面,如下面的代码片段所示:
| 1 2 3 4 5 6 |
glBegin(GL_QUADS);
glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f);
glTexCoord2f(3.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f);
glTexCoord2f(3.0f, 3.0f); glVertex3f( 1.0f, 1.0f, 1.0f);
glTexCoord2f(0.0f, 3.0f); glVertex3f(-1.0f, 1.0f, 1.0f);
glEnd();
|
3.2.7. 清除纹理对象
清除纹理对象的绑定,它们的数据可能还保存在纹理资源的,但是如果纹理资源有限的话,删除纹理显然是释放纹理资源有效的方法之一,清除纹理对象的接口是glDeleteTextures()。
| 1 |
void glDeleteTextures(GLsizei n,const GLuint* textures);
|
3.2.8. 代码示例
简单的纹理贴图代码示例和演示效果图如下所示:

图22. 简单的二维纹理贴图
其中的主体代码文件texture-base-demo.cpp中的代码如下所示:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 |
/************************************************************************
\link www.twinklingstar.cn
\author Twinkling Star
\date 2013/11/30
\file texture-base-demo.cpp
****************************************************************************/
#include
#include
#include
#pragma comment(lib,"opengl32.lib")
#pragma comment(lib,"glu32.lib")
#include
#include // Header File For The OpenGL32 Library
#include // Header File For The GLu32 Library
#include // Header File For The Glaux Library
#include "SrImageBmp.h"
SrImageBmp g_textureBMP(IMAGE_READ_ONLY);
unsigned int g_textureId;
void drawScene()
{
//激活纹理
glBindTexture(GL_TEXTURE_2D, g_textureId);
//绘制一个正方体
glBegin(GL_QUADS);
// Front Face
glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f);
glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f);
glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, 1.0f);
glTexCoord2f(0.0f, 1.0f); glVertex3f(-1.0f, 1.0f, 1.0f);
// Back Face
glTexCoord2f(1.0f, 0.0f); glVertex3f(-1.0f, -1.0f, -1.0f);
glTexCoord2f(1.0f, 1.0f); glVertex3f(-1.0f, 1.0f, -1.0f);
glTexCoord2f(0.0f, 1.0f); glVertex3f( 1.0f, 1.0f, -1.0f);
glTexCoord2f(0.0f, 0.0f); glVertex3f( 1.0f, -1.0f, -1.0f);
// Top Face
glTexCoord2f(0.0f, 1.0f); glVertex3f(-1.0f, 1.0f, -1.0f);
glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, 1.0f, 1.0f);
glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, 1.0f, 1.0f);
glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, -1.0f);
// Bottom Face
glTexCoord2f(1.0f, 1.0f); glVertex3f(-1.0f, -1.0f, -1.0f);
glTexCoord2f(0.0f, 1.0f); glVertex3f( 1.0f, -1.0f, -1.0f);
glTexCoord2f(0.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f);
glTexCoord2f(1.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f);
// Right face
glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, -1.0f, -1.0f);
glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, -1.0f);
glTexCoord2f(0.0f, 1.0f); glVertex3f( 1.0f, 1.0f, 1.0f);
glTexCoord2f(0.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 1.0f);
// Left Face
glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, -1.0f, -1.0f);
glTexCoord2f(1.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 1.0f);
glTexCoord2f(1.0f, 1.0f); glVertex3f(-1.0f, 1.0f, 1.0f);
glTexCoord2f(0.0f, 1.0f); glVertex3f(-1.0f, 1.0f, -1.0f);
glEnd();
}
void draw(void)
{
glMatrixMode(GL_MODELVIEW);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // Clear The Screen And The Depth Buffer
glLoadIdentity(); // Reset The View
glTranslatef(0.0f,0.0f,-5.0f);
glRotatef(45.0f,1.0f,1.0f,1.0f);
drawScene();
glFlush();
}
void initTexture()
{
unsigned char* data;
int pixelCount,rgbType;
if( !g_textureBMP.readFile("NeHe.bmp",data,pixelCount,rgbType) )
{
return;
}
int internalFormat,format;
if( rgbType == IMAGE_RGB)
{
internalFormat = 3;
format = GL_RGB;
}
else if( rgbType == IMAGE_RGBA )
{
internalFormat = 4;
format = GL_RGBA;
}
//生成纹理名字
glGenTextures(1, &g_textureId);
//绑定纹理
glBindTexture(GL_TEXTURE_2D, g_textureId);
//存储纹理数据到硬件内存中
glTexImage2D(GL_TEXTURE_2D, 0, 3, g_textureBMP.getWidth(), g_textureBMP.getHeight(), 0, GL_RGB, GL_UNSIGNED_BYTE, data);
//设置纹理放大缩小时的过滤方法
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_LINEAR);
}
void init()
{
glClearColor(0.0f,0.0f,0.0f,0.0f);
glEnable(GL_DEPTH_TEST);
glEnable(GL_TEXTURE_2D);
initTexture();
}
void reshape(GLsizei w,GLsizei h)
{
glViewport(0,0,w,h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0f,(float)w/(float)h,1.0f,1000.0f);
}
int main(int argc,char ** argv)
{
glutInit(&argc,argv);
glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);
glutInitWindowSize(400,400);
glutCreateWindow("texture-base-demo");
init();
glutReshapeFunc(reshape);
glutDisplayFunc(draw);
glutMainLoop();
return(0);
}
|
多重细节层纹理的应用示例代码和演示效果图如下所示:

图23. mipmap应用示例,按空格键,会将摄像头往后移,导致渲染的正方形越来越小,使得不同的图像大小,对应不同的纹理细节层
代码texture-mipmap-demo.cpp的代码如下所示:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 |
/************************************************************************
\link www.twinklingstar.cn
\author Twinkling Star
\date 2013/11/30
****************************************************************************/
#include
#include
#include
#pragma comment(lib,"opengl32.lib")
#pragma comment(lib,"glu32.lib")
#include
#include // Header File For The OpenGL32 Library
#include // Header File For The GLu32 Library
#include // Header File For The Glaux Library
GLubyte mipmapImage512[512][512][4];
GLubyte mipmapImage256[256][256][4];
GLubyte mipmapImage128[128][128][4];
GLubyte mipmapImage64[64][64][4];
GLubyte mipmapImage32[32][32][4];
GLubyte mipmapImage16[16][16][4];
GLubyte mipmapImage8[8][8][4];
GLubyte mipmapImage4[4][4][4];
GLubyte mipmapImage2[2][2][4];
GLubyte mipmapImage1[1][1][4];
static GLuint texName;
int distance = -5.0f;
void makeImages(void)
{
int i, j;
for (i = 0; i < 512; i++) {
for (j = 0; j < 512; j++) {
mipmapImage512[i][j][0] = 255;
mipmapImage512[i][j][1] = 255;
mipmapImage512[i][j][2] = 255;
mipmapImage512[i][j][3] = 255;
}
}
for (i = 0; i < 256; i++) {
for (j = 0; j < 256; j++) {
mipmapImage256[i][j][0] = 255;
mipmapImage256[i][j][1] = 0;
mipmapImage256[i][j][2] = 0;
mipmapImage256[i][j][3] = 255;
}
}
for (i = 0; i < 128; i++) {
for (j = 0; j < 128; j++) {
mipmapImage128[i][j][0] = 0;
mipmapImage128[i][j][1] = 255;
mipmapImage128[i][j][2] = 0;
mipmapImage128[i][j][3] = 255;
}
}
for (i = 0; i < 64; i++) {
for (j = 0; j < 64; j++) {
mipmapImage64[i][j][0] = 0;
mipmapImage64[i][j][1] = 0;
mipmapImage64[i][j][2] = 255;
mipmapImage64[i][j][3] = 255;
}
}
for (i = 0; i < 32; i++) {
for (j = 0; j < 32; j++) {
mipmapImage32[i][j][0] = 255;
mipmapImage32[i][j][1] = 255;
mipmapImage32[i][j][2] = 0;
mipmapImage32[i][j][3] = 255;
}
}
for (i = 0; i < 16; i++) {
for (j = 0; j < 16; j++) {
mipmapImage16[i][j][0] = 255;
mipmapImage16[i][j][1] = 0;
mipmapImage16[i][j][2] = 255;
mipmapImage16[i][j][3] = 255;
}
}
for (i = 0; i < 8; i++) {
for (j = 0; j < 8; j++) {
mipmapImage8[i][j][0] = 255;
mipmapImage8[i][j][1] = 0;
mipmapImage8[i][j][2] = 0;
mipmapImage8[i][j][3] = 255;
}
}
for (i = 0; i < 4; i++) {
for (j = 0; j < 4; j++) {
mipmapImage4[i][j][0] = 0;
mipmapImage4[i][j][1] = 255;
mipmapImage4[i][j][2] = 0;
mipmapImage4[i][j][3] = 255;
}
}
for (i = 0; i < 2; i++) {
for (j = 0; j < 2; j++) {
mipmapImage2[i][j][0] = 0;
mipmapImage2[i][j][1] = 0;
mipmapImage2[i][j][2] = 255;
mipmapImage2[i][j][3] = 255;
}
}
mipmapImage1[0][0][0] = 255;
mipmapImage1[0][0][1] = 255;
mipmapImage1[0][0][2] = 255;
mipmapImage1[0][0][3] = 255;
}
void initTexture(void)
{
makeImages();
//生成纹理名字
glGenTextures(1, &texName);
//将纹理名字与纹理绑定
glBindTexture(GL_TEXTURE_2D, texName);
//设置当纹理坐标超过1后,纹理在s,t方向上的模式
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
//设置纹理图像放大时,采用的过滤方法
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER,GL_NEAREST);
//设置纹理图像缩小时,采用的过滤方法
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST_MIPMAP_NEAREST);
//从0到9,指定了10个纹理细节层
int level = 0;
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 512, 512, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage512);
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 256, 256, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage256);
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 128, 128, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage128);
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 64, 64, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage64);
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 32, 32, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage32);
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 16, 16, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage16);
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 8, 8, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage8);
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 4, 4, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage4);
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 2, 2, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage2);
glTexImage2D(GL_TEXTURE_2D, level++, GL_RGBA, 1, 1, 0,
GL_RGBA, GL_UNSIGNED_BYTE, mipmapImage1);
//激活二维纹理的使用
glEnable(GL_TEXTURE_2D);
}
void drawScene()
{
//激活纹理
glBindTexture(GL_TEXTURE_2D, texName);
//绘制一个正方形
glBegin(GL_QUADS);
glTexCoord2f(0.0f, 0.0f); glVertex3f(-1.0f, -1.0f, 0.0f);
glTexCoord2f(1.0f, 0.0f); glVertex3f( 1.0f, -1.0f, 0.0f);
glTexCoord2f(1.0f, 1.0f); glVertex3f( 1.0f, 1.0f, 0.0f);
glTexCoord2f(0.0f, 1.0f); glVertex3f(-1.0f, 1.0f, 0.0f);
glEnd();
}
void draw(void)
{
glMatrixMode(GL_MODELVIEW);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
glTranslatef(0.0f,0.0f,distance);
drawScene();
glFlush();
}
void keyboards(unsigned char key, int x, int y)
{
switch (key) {
case 27:
exit(0);
break;
case ' ':
distance -= 2.0f;
glutPostRedisplay();
break;
default:
break;
}
}
void init()
{
glClearColor(0.0f,0.0f,0.0f,0.0f);
glEnable(GL_DEPTH_TEST);
initTexture();
}
void reshape(GLsizei w,GLsizei h)
{
glViewport(0,0,w,h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0f,(float)w/(float)h,1.0f,1000.0f);
}
int main(int argc,char ** argv)
{
glutInit(&argc,argv);
glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);
glutInitWindowSize(400,400);
glutCreateWindow("texture-mipmap-demo");
init();
glutReshapeFunc(reshape);
glutDisplayFunc(draw);
glutKeyboardFunc(keyboards);
glutMainLoop();
return(0);
}
|
4. 光照
OpenGL中应用到的光照模型称为Phong光照模型,它能够模拟出光照的效果,但是它不是基于真实的物理原理,可能导致渲染出的光照效果不太真实。Blinn(1977)[17],Cook&Torrance(1982)[18]提出基于物理光照原理的模型,但这不作为本节讨论的内容。
4.1. Phong光照模型

图24. 有光照效果和没有关照效果的球
如图24所示,是一个在三维的空间上有光照和没有光照的球的对比图,可以看出光照在构造三维场景的重要性。一个平面的光反射过程是复杂的,依赖很多的因素,包括光源的方向,观察者的位置,平面的法向量,平面本身的性质,比如颜色、粗糙程度。着色模型规定了光照通过平面后如何发散的。先考虑简单的光照,无彩光(Achromatic Light),即只有亮度没有颜色的光,接着再拓展有颜色的光和有颜色的平面的情况。
照向平面的入射光,主要有三个去向:(1)被平面吸收,转化为热能;(2)被平面反射;(3)发送到平面内部,此时的平面就像一块玻璃。如果光线完全被吸收,那么就成为了一个黑洞。Phong 光照模型是由Phong(1975)[15]提出的,Phong光照模型只会考虑第(2)种情况,入射光的反射主要包括两种情况:漫反射和镜面反射。
4.1.1. 漫反射光(Diffuse Light)

图25. 一束射向平面
如图25所示,一束光射向平面上的点P,计算由点P射向眼睛的漫反射量。法向量m→是平面在P点位置的向量,v→是P点到眼睛向量,s→是P点到光源的向量。漫反射分量向各个方向发散,每个方向的发散量是均等的,所以平面相对于眼睛的朝向是没有意义的,它与向量m→和向量s→的夹角相关。如图26左图所示,如果一束光射向平面,光的方向与平面的法向量平行,则在该方向上的漫反射分量最大;如图26右图所示,如果光射向平面,光的方向与平面的法向量呈一定的夹角,则漫反射最随着夹角的变大而减少。Phong光照模型定义了一个公式来计算漫反射量:
Id=Isρdmax(s→⋅m→∣∣s→∣∣∣∣m→∣∣,0) (19)
其中,Id表示光源的强度,ρd表示漫反射系数(Diffuse Reflection Coefficient),当m→与s→的点积为负,则夹角θ>90,此时漫反射分量为0。
现实世界中,漫反射过程比采用的模型复杂非常的多,漫反射系数的取值依赖入射光的波长(即颜色),角度θ,平面的物理属性,为了简化计算,那些因素都被排除了。
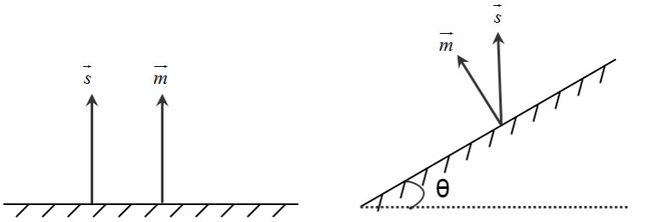
图26. 漫反射亮度依赖角度θ
4.1.2. 镜面反射光(Specular Light)

图27. 镜面反射
如图27所示,一束光射向平面上的点P,计算由点P射向眼睛的镜面反射量。法向量m→是平面在P点位置的向量,v→是P点到眼睛向量,m→是P点到光源的向量,r→是镜面反射的方向,方向r→只与向量m→、m→有关,可以得到等式(20),Φ是r→与v→的夹角,进入人眼的镜面反射光的多少与夹角Φ有关,Φ越大,进入人眼的反射光线越少。
r→=−s→+2(s→⋅m→)∣∣m→∣∣2m→(20)
Phong光照模型定义了一个公式来计算镜面反射量Isp:
Isp=Isρs(cos(ϕ))f=Isρs(r→∣∣r→∣∣⋅v→∣∣v→∣∣)f (21)
f的取值通常在1到200之间,f的取值越大,镜面反射光越集中在向量r→的附近。不同的f取值下,Φ与cos(Φ)f的关系图,如图28所示。ρs表示镜面反射系数(Specular Reflection Coefficient),它的取值往往是跟据实验结果确定的。
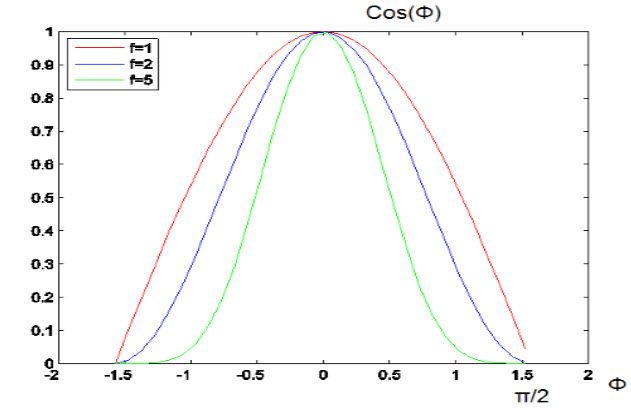
图28. 镜面反射量随着角度Φ的增大而衰减
如果r→与v→的点积为负,则镜面反射分量Isp为0。如果计算镜面反射量时,都需要计算r→,再代入,则计算很费时。可以采用半角向量(Halfway Vector)进行加速的方向,如图29所示,h→=s→+v→,如果向量m→,s→,v→共面,则有Φ=2β,可自行推导。最终的镜面反射量,可以采用等式(22)来确定。
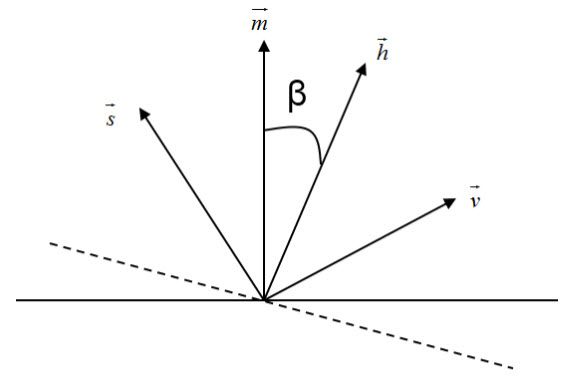
图29. 半角向量
Isp=Isρsmax⎛⎝⎜⎛⎝⎜h→∣∣∣h→∣∣∣⋅m→∣∣m→∣∣⎞⎠⎟f,0⎞⎠⎟ (22)
4.1.3. 环境光(Ambient Light)
为了避免完全黑暗阴影的情况,引入环境光,环境光不放置在某一固定位置,并且统一向各个方法传播,环境光的强度为Ia。在这种模型下,每个平面都分配有一个环境反射系数(Ambient Reflection Coefficient)ρa。环境光分量Iaρa与漫射光分量、镜面光分量相加,就得到传入眼中的反射光。
4.1.4. 组合光
组合上述三种光的贡献,就得到传入人眼中的反射光I,组合后的等式为:
I=Iaρa+Idρd⋅lambert+Isρs⋅phongf,lambert=max(0,s→⋅m→∣∣s→∣∣∣∣m→∣∣),phong=max⎛⎝⎜0,h→⋅m→∣∣∣h→∣∣∣⋅∣∣m→∣∣⎞⎠⎟(23)
组合上述三种光的贡献,就得到传入人眼中的反射光I,组合后的等式为:
4.1.5. 有色光
前面只考虑光强,没有考虑有色光。分别计算R,G,B,调用三次等式(23),如等式(24)所示。此时形成9个反射系数,通常情况下,漫射光和反射光是相同,漫射光系数和环境光系数基于平面本身的颜色,如果平面是红色的,在白光的反射下就显得是红色的。
Ir=Iarρar+Idrρdr×lambert+Isprρsr×phongfIg=Iagρag+Idgρdg×lambert+Ispgρsg×phongfIb=Iabρab+Idbρdb×lambert+Ispbρsb×phongf(24)
其中,lambert=max(0,s→⋅m→∣∣s→∣∣∣∣m→∣∣),phong=max⎛⎝⎜0,h→⋅m→∣∣∣h→∣∣∣⋅∣∣m→∣∣⎞⎠⎟。
4.1.6. 聚光灯
如图30所示,就是真实世界的聚光灯。在图形学领域,聚光灯后面的数学模型是什么呢?这就是本节考虑的问题,如图31所示,就是聚光灯的数学模型示意图,在角度超过α的截锥外没有任何光线,对于角度为β的光线量随着一定的比例衰减,可以把定义比例系数为cosε(β),β表示由聚光灯的方向d→与聚光灯射向平面上的点P的光线之间的夹角。随着距离的增加,光照强度会逐渐减弱,衰减公式可以表示为:
atten=1kc+klD+kqD2(25)
其中,kc,kl,kq是比例系数,D表示光源与点P的距离。
那么由聚光灯射向点P的光线强度可以计算为:
Ispot=I1kc+klD+kqD2cosε(β) (26)
其中,I表示聚光灯的原始光强。

图30. 真实世界的聚光灯
 图31. 聚光灯的数学模型示意图
图31. 聚光灯的数学模型示意图
4.1.7. 光照公式总结
除了漫反射光、镜面反射光、环境光和聚光灯外,我们还需要增加一个全局环境光和自发光(Emissive Light),全局环境光和自发光与具体的光源是相互独立的。至此,我们可以得到最终的光照计算公式:
I=e+Iglobalρa+∑iatteni⋅spoti⋅(Iiaρa+Iij,dρd⋅lamberti+Iisρs⋅phongfi) (27)
其中,lambert=max(0,s→⋅m→∣∣s→∣∣∣∣m→∣∣),phong=max⎛⎝⎜0,h→⋅m→∣∣∣h→∣∣∣∣∣m→∣∣⎞⎠⎟,j∈{r,g,b},i={0....7}, spoti=cos(β)ε,atten=1kc+klD+kqD2,i表示光源,e表示自发光,Iglobalρa表示全局环境光。
4.2. 光照的应用
4.2.1. 简单的光源
OpenGL允许定义最多8个光源,依次命名为GL_LIGHT0,GL_LIGHT1等等,可以赋予每个光源不同的属性,设置属性的接口为glLight*():
| 1 2 3 4 |
void glLightf( GLenum light, GLenum pname, GLfloat param);
void glLighti( GLenum light, GLenum pname, GLint param);
void glLightfv( GLenum light, GLenum pname, const GLfloat * params);
void glLightiv( GLenum light, GLenum pname, const GLint * params);
|
其中,pname可以用到的参数为:
| 1 2 3 4 5 6 7 8 9 10 |
GL_AMBIENT
GL_DIFFUSE
GL_SPECULAR
GL_POSITION
GL_SPOT_CUTOFF
GL_SPOT_DIRECTION
GL_SPOT_EXPONENT
GL_CONSTANT_ATTENUATION
GL_LINEAR_ATTENUATION
GL_QUADRATIC_ATTENUATION
|
光源有默认的值,对于GL_LIGHT0光源,GL_DIFFUSE和GL_SPECULAR默认的值为(1.0,1.0,1.0,1.0),光源默认的位置为(0,0,0,1.0)。默认情况下,OpenGL是关闭光源功能的,所以我们需要激活光照功能,并且要激活指定的光源。简单的代码片段如下所示:
| 1 2 |
glEnable(GL_LIGHT0); //激活指定光源
glEnable(GL_LIGHTING); //激活光源功能
|
简单的代码示例如下所示,如等式(27)所示,相当于指定了镜面反射光强Is、环境光强Ia和漫反射光强Id,当然光强也分为R、G、B三元色。
| 1 2 3 4 5 6 7 8 9 |
GLfloat LightSpeclar[] = { 0.75f, 0.75f, 0.75f, 1.0f }; //镜面反射分量
GLfloat LightAmbient[] = { 0.1f, 0.1f, 0.1f, 1.0f }; //环境光分量
GLfloat LightDiffuse[] = { 0.5f, 0.5f, 0.5f, 1.0f }; //漫反射分量
GLfloat LightPosition[] = { 0.0f, 0.0f, 0.0f, 1.0f }; //光照的位置
glLightfv(GL_LIGHT0, GL_SPECULAR, LightSpeclar);
glLightfv(GL_LIGHT0, GL_AMBIENT, LightAmbient);
glLightfv(GL_LIGHT0, GL_DIFFUSE, LightDiffuse);
glLightfv(GL_LIGHT0, GL_POSITION,LightPosition);
|
后面的6个参数与聚光灯相关, GL_SPOT_CUTOFF规定了图31中所示的聚光灯的最大角α,GL_SPOT_DIRECTION规定了聚光灯的方向向量d→,GL_SPOT_EXPONENT规定了比例系数ε,GL_CONSTANT_ATTENUATION, GL_LINEAR_ATTENUATION, GL_QUADRATIC_ATTENUATION则规定了聚光灯的衰减系数。
接着,介绍反射系数的设置。选择不同的反射系数,可以使对象显示由不同的材质做成的,采用接口glMaterial()来指定材质,即指定不同的反射系数,相当于指定三种光的反射系数ρ。
| 1 2 3 4 |
void glMaterialf( GLenum face, GLenum pname, GLfloat param);
void glMateriali( GLenum face, GLenum pname, GLint param);
void glMaterialf( GLenum face, GLenum pname, GLfloat param);
void glMateriali( GLenum face, GLenum pname, GLint param);
|
如果参数pname分别选择为GL_SPECULAR,GL_DIFFUSE,GL_AMBIENT, 相当于设置材质的镜面反射系数、漫反射系数和环境光反射系数。
如果参数pname选择为GL_SHININESS,它指定的值在数学模型上相当于等式(27)中的变量f,取值范围是[0,128]。镜面反射可能在对象表面形成一块强光区(Highlight),能观察到的镜面反射量与观察者的位置有关,例如观察一个被太阳光照射的金属小球,随着观察者的移动,强光区也会一定程度上发生移动。通过对变量f的取值,可以控制强光区的尺寸和亮度,值越大,强光区越小,越亮。
如果参数pname选择为GL_EMISSION,为自发光分配一个RGBA的颜色值,能使一个对象显现出正在释放该种颜色的光线样子,然而它并非真正扮演了光源的效果,我们可以使用这种特征去仿真台灯等,相当于等式(27)中的变量e的值。
反射系数的代码片段如下所示:
| 1 2 3 4 5 6 7 |
GLfloat MaterialSpecular[] = {0.508273f, 0.508273f, 0.508273f, 1.0f};
GLfloat MaterialDiffuse[] = {0.50754f, 0.50754f, 0.50754f, 1.0f};
GLfloat MaterialAmbient[] = {0.19225f, 0.19225f, 0.19225f, 1.0f};
glMaterialfv(GL_FRONT_AND_BACK, GL_SPECULAR, MaterialSpecular);
glMaterialfv(GL_FRONT_AND_BACK, GL_DIFFUSE, MaterialDiffuse);
glMaterialfv(GL_FRONT_AND_BACK, GL_AMBIENT, MaterialAmbient);
glMaterialf(GL_FRONT_AND_BACK, GL_SHININESS, 51.2f);
|
此外,还一个与全局光照相关的设置函数glLightModel*(),规定一些应用光照模型的规则。GL_LIGHT_MODEL_AMBIENT,创建全局的环境光,默认值为(0.2, 0.2,0.2, 1.0);GL_LIGHT_MODEL_LOCAL_VIEWER,OpenGL计算镜面反射时采用的是半角向量h→�=s→�+v→,不同顶点上的向量s→和v→都不同。如果光源是方向性的,则s→是常量,但是v→随着顶点的不同而改变。如果对于所有的点,v→是一个常量,渲染的速度会提高,v→的默认值为(0,0,1)。
如果我们需要渲染有颜色的材质,例如采用接口glColor3f()渲染一个红色的小球,需要激活颜色材质:
| 1 |
glEnable(GL_COLOR_MATERIAL);
|
简单的光照示例代码和演示效果如下所示:

图32. 光照效果的小球
代码文件light-demo.cpp的代码如下所示:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
/************************************************************************
\link www.twinklingstar.cn
\author Twinkling Star
\date 2015/02/03
\file light-demo.cpp
****************************************************************************/
#include
#include
#include
#pragma comment(lib,"opengl32.lib")
#pragma comment(lib,"glu32.lib")
#include
#include // Header File For The OpenGL32 Library
#include // Header File For The GLu32 Library
#include // Header File For The Glaux Library
void drawSpherical(float x, float y, float z)
{
static GLUquadricObj *quadratic = NULL;
if( !quadratic )
quadratic=gluNewQuadric(); // Create A Pointer To The Quadric Object (Return 0 If No Memory)
gluQuadricNormals(quadratic, GLU_SMOOTH); // Create Smooth Normals
//glEnable(GL_COLOR_MATERIAL);
glPushAttrib(GL_ENABLE_BIT);
glPushMatrix();
//glColor3f(1.0f, 0.0f, 0.0f);
glTranslatef(x, y, z);
gluSphere(quadratic,1.3f,32,32);
glPopMatrix();
glPopAttrib();
}
void draw(void)
{
glMatrixMode(GL_MODELVIEW);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
glTranslatef(0.0f,0.0f,-5.0f);
drawSpherical(0,0,0);
glFlush();
}
void init()
{
glClearColor(0.0f,0.0f,0.0f,0.0f);
glEnable(GL_DEPTH_TEST);
GLfloat LightSpeclar[] = { 1.0f, 1.0f, 1.0f, 1.0f }; //镜面反射分量
GLfloat LightAmbient[] = { 0.1f, 0.1f, 0.1f, 1.0f }; //环境光分量
GLfloat LightDiffuse[] = { 0.7f, 0.7f, 0.7f, 1.0f }; //漫反射分量
GLfloat LightPosition[] = { 0.0f, 0.0f, 3.0f, 1.0f }; //光照的位置
glLightfv(GL_LIGHT0, GL_SPECULAR, LightSpeclar);
glLightfv(GL_LIGHT0, GL_AMBIENT, LightAmbient);
glLightfv(GL_LIGHT0, GL_DIFFUSE, LightDiffuse);
glLightfv(GL_LIGHT0, GL_POSITION,LightPosition);
GLfloat MaterialSpecular[] = {0.508273f, 0.508273f, 0.508273f, 1.0f};
GLfloat MaterialDiffuse[] = {0.50754f, 0.50754f, 0.50754f, 1.0f};
GLfloat MaterialAmbient[] = {0.19225f, 0.19225f, 0.19225f, 1.0f};
glMaterialfv(GL_FRONT_AND_BACK, GL_SPECULAR, MaterialSpecular);
glMaterialfv(GL_FRONT_AND_BACK, GL_DIFFUSE, MaterialDiffuse);
glMaterialfv(GL_FRONT_AND_BACK, GL_AMBIENT, MaterialAmbient);
glMaterialf(GL_FRONT_AND_BACK, GL_SHININESS, 51.2f);
glEnable(GL_LIGHT0);
glEnable(GL_LIGHTING);
}
void reshape(GLsizei w,GLsizei h)
{
glViewport(0,0,w,h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0f,(float)w/(float)h,1.0f,1000.0f);
}
int main(int argc,char ** argv)
{
glutInit(&argc,argv);
glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);
glutInitWindowSize(400,400);
glutCreateWindow("light-demo");
init();
glutReshapeFunc(reshape);
glutDisplayFunc(draw);
glutMainLoop();
return(0);
}
|
5. 着色模型
前面的光照模型考虑的是某个点的反射光计算,着色模型考虑的是整个面的反射光的计算。本小节介绍OpenGL两种着色模型:平面着色(Flat Shading)和平滑着色(Smooth Shading)。平面着色模型可能会引发马赫带等问题,而平滑着色的目的是通过计算每个平面上更多的点,来淡化平面之间的边。平滑着色中又包括两类着色模型:Gouraud着色模型[16]和Phong着色模型[15]。
5.1. 平面着色
计算机上无法画出完全弯曲的曲面,只能把曲面细分成足够小的平面,使得人眼能“误”把它当成一个曲面。采用平面着色模型,相当于规定每个平面任意一个点的法向量相同,那么整个平面上光照的漫反射量一样的,造成使用同一个颜色覆盖整个平面上的像素。由于不同平面之间的不连续,容易形成马赫带(Mach Band),如图33所示。

图33. 存在马赫带的小球和光滑的小球
在平面着色模式下,镜面反射的强光区被渲染的效果也非常的差,因为只用一种颜色填充一个平面,即只有一个顶点被计算,如果在平面的代表顶点上有镜面反射的强光效果,则该平面就会统一出现这种效果,相反,如果强光区没有落在平面的代表点上,则整个平面完全没有强光效果,如图34所示。

图34. 带有强光区的平面着色和平滑着色
5.2. Gouraud着色
Gouraud着色采用简单的线性插值的方法来淡化边。以图35为例,图中的四个顶点表示一个平面的边界点,四个顶点的坐标分别为(x1,y1),(x2,y2),(x3,y3),(x4,y4),现在要计算扫描线y上的颜色值,扫描线与四边形相交于点p1,p2,首先利用线性插值的方法计算出点p1的颜色值,由比例关系得:
y−y1y4−y1=colorp1−color1color4−color1
可以计算出点p1的颜色值,同理,可以计算出点p2的颜色值。最后,再对扫描线y上,在[xleft,xright]范围内的颜色进行线性插值。

图35. Gouraud着色原理
在绘制球体时,该方法消除了马赫带效应,OpenGL中也是支持Gouraud着色的。然而每个像素的颜色是通过线性插值的方法得到的,没有采用任何与物理定律有关的计算,因此Gouraud着色在显示强光区上的性能并不真实,然而Phong着色就能更好的显示强光区。
5.3. Phong着色
Phong着色模型是对法向量进行线性插值,计算出每个像素的法向量,再根据法向量计算颜色。该方法的一个很大的缺点是,运算复杂费时,效率低。OpenGL无法支持该着色模型,因为向量信息无法传递到透视变换、透视除法之后的渲染阶段。
5.4. 代码
代码示例和演示效果图如下所示,运行程序,按空格键,会在平面着色和光滑着色之间进行切换:

图36. 平面着色和光滑着色的示例
代码文件shading-model-demo.cpp如下所示:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
/************************************************************************
\link www.twinklingstar.cn
\author Twinkling Star
\date 2015/02/03
\file shading-model-demo.cpp
****************************************************************************/
#include
#include
#include
#pragma comment(lib,"opengl32.lib")
#pragma comment(lib,"glu32.lib")
#include
#include // Header File For The OpenGL32 Library
#include // Header File For The GLu32 Library
#include // Header File For The Glaux Library
void drawSpherical(float x, float y, float z)
{
static GLUquadricObj *quadratic = NULL;
if( !quadratic )
quadratic=gluNewQuadric(); // Create A Pointer To The Quadric Object (Return 0 If No Memory)
gluQuadricNormals(quadratic, GLU_SMOOTH); // Create Smooth Normals
glPushAttrib(GL_ENABLE_BIT);
glPushMatrix();
glTranslatef(x, y, z);
gluSphere(quadratic,1.3f,32,32);
glPopMatrix();
glPopAttrib();
}
void setHighlight()
{
GLfloat MaterialSpecular[] = {0.508273f, 0.508273f, 0.508273f, 1.0f};
GLfloat MaterialDiffuse[] = {0.50754f, 0.50754f, 0.50754f, 1.0f};
GLfloat MaterialAmbient[] = {0.19225f, 0.19225f, 0.19225f, 1.0f};
glMaterialfv(GL_FRONT_AND_BACK, GL_SPECULAR, MaterialSpecular);
glMaterialfv(GL_FRONT_AND_BACK, GL_DIFFUSE, MaterialDiffuse);
glMaterialfv(GL_FRONT_AND_BACK, GL_AMBIENT, MaterialAmbient);
glMaterialf(GL_FRONT_AND_BACK, GL_SHININESS, 51.2f);
}
void setNormal()
{
GLfloat MaterialSpecular[] = {0.0f, 0.0f, 0.0f, 1.0f};
GLfloat MaterialDiffuse[] = {0.8f, 0.8f, 0.8f, 1.0f};
GLfloat MaterialAmbient[] = {0.2f, 0.2f, 0.2f, 1.0f};
glMaterialfv(GL_FRONT_AND_BACK, GL_SPECULAR, MaterialSpecular);
glMaterialfv(GL_FRONT_AND_BACK, GL_DIFFUSE, MaterialDiffuse);
glMaterialfv(GL_FRONT_AND_BACK, GL_AMBIENT, MaterialAmbient);
glMaterialf(GL_FRONT_AND_BACK, GL_SHININESS, 1.0f);
}
void draw(void)
{
glMatrixMode(GL_MODELVIEW);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
//带有强光区的小球
setHighlight();
glLoadIdentity();
glTranslatef(-2.0f,0.0f,-5.0f);
drawSpherical(0,0,0);
//不存在强光区的小球
setNormal();
glLoadIdentity();
glTranslatef(2.0f,0.0f,-5.0f);
drawSpherical(0,0,0);
glFlush();
}
bool gIsSmooth = true;
void keyboards(unsigned char key, int x, int y)
{
switch (key) {
case 27:
exit(0);
break;
case ' ':
gIsSmooth = !gIsSmooth;
if(gIsSmooth)
glShadeModel(GL_SMOOTH);
else
glShadeModel(GL_FLAT);
glutPostRedisplay();
break;
default:
break;
}
}
void init()
{
glClearColor(0.0f,0.0f,0.0f,0.0f);
GLfloat LightSpeclar[] = { 1.0f, 1.0f, 1.0f, 1.0f }; //镜面反射分量
GLfloat LightAmbient[] = { 0.1f, 0.1f, 0.1f, 1.0f }; //环境光分量
GLfloat LightDiffuse[] = { 0.7f, 0.7f, 0.7f, 1.0f }; //漫反射分量
GLfloat LightPosition[] = { 0.0f, 0.0f, 3.0f, 1.0f }; //光照的位置
glLightfv(GL_LIGHT0, GL_SPECULAR, LightSpeclar);
glLightfv(GL_LIGHT0, GL_AMBIENT, LightAmbient);
glLightfv(GL_LIGHT0, GL_DIFFUSE, LightDiffuse);
glLightfv(GL_LIGHT0, GL_POSITION,LightPosition);
glEnable(GL_LIGHT0);
glEnable(GL_DEPTH_TEST);
glEnable(GL_LIGHTING);
}
void reshape(GLsizei w,GLsizei h)
{
glViewport(0,0,w,h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0f,(float)w/(float)h,1.0f,1000.0f);
}
int main(int argc,char ** argv)
{
glutInit(&argc,argv);
glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);
glutInitWindowSize(800,400);
glutCreateWindow("shading-model-demo");
init();
glutReshapeFunc(reshape);
glutDisplayFunc(draw);
glutKeyboardFunc(keyboards);
glutMainLoop();
return(0);
}
|
6. 回顾顶点渲染管线

图37. 顶点渲染管线
回顾下顶点处理管线,如图37所示,在不同的阶段,对管线中的数据进行分析:
(1)一个顶点包括坐标信息、纹理坐标信息、法向量信息V,s,t,n⃗ ,经过模型视图变换,形成摄像机坐标系统下的坐标信息、法向量信息,纹理坐标信息A,sA,tA,n⃗ ′,其中,只有纹理坐标未发生改变;
(2)使用向量信息,进行着色计算,生成颜色信息C,此时向量信息已经转化为颜色信息,不再保存向量值,结果得到的是A,sA,tA,C,参见第5节。
(3)接着进行透视变换,生成齐次坐标a~=(a1,a2,a3,a4),纹理坐标信息和颜色信息不变,即得到的信息是a~,sA,tA,C;
(4)裁剪操作,将不在CVV范围内的图元裁剪掉,只留下CVV范围内的图元;
(5)后面通过透视除法,生成如图所示的几个变量a1a4,a2a4,a3a4,sAa4,tAa4,C,1a4,这些变量在纹理映射中会被采用,纹理映射是发生在透视除法之后,参见第3节。
参 考
[1] Shreiner Dave. Opengl Programming Guide: The Official Guide To Learning Opengl, Version 2.1, 6/E. Pearson Education India, 2008.
[2] Wikipedia. “OpenGL”. website < http://en.wikipedia.org/wiki/OpenGL>.
[3] Songho. “OpenGL”. website < http://www.songho.ca/opengl>.
[4] OpenGL. webite .
[5] The OpenGL Utility Toolkit. website .
[6] Chua Hock-Chuan. “3D Graphics with OpenGL Basic Theory”. website .
[7] F. Hill, and S. Kelley. Computer Graphics Using OpenGL, 2/E. Pearson, 2004.
[8] Mike Cyrus, and Jay Beck. "Generalized two-and three-dimensional clipping."Computers & Graphics, vol.3, no.1, pp.23-28, 1978.
[9] You-Dong Liang, and Brian A. Barsky. "A new concept and method for line clipping." ACM Transactions on Graphics (TOG), vol.3, no.1, pp.1-22, 1984.
[10] Brian A. Barsky, You Liang, and Mel Slater. "Some Improvements to a Parametric Line Clipping Algorithm." 1992.
[11] Sobkow, Mark S., Paul Pospisil, and Yee-Hong Yang. "A fast two-dimensional line clipping algorithm via line encoding." Computers & graphics, vol.11, no.4, pp.459-467, 1987.
[12] Tina M. Nicholl, D. T. Lee, Robin A. Nicholl. "An efficient new algorithm for 2-D line clipping: Its development and analysis". SIGGRAPH '87, pp.253–262, 1987.
[13] Jim Blinn. Jim Blinn's corner: a trip down the graphics pipeline. Morgan Kaufmann, 1996.
[14] Lance Williams. "Pyramidal parametrics." ACM Siggraph Computer Graphics. Vol. 17. No. 3. ACM, 1983.
[15] Bui Tuong Phong. "Illumination for computer generated pictures." Communications of the ACM, vol.18, no.6, pp.311-317, 1975.
[16] Henri Gouraud. "Continuous shading of curved surfaces." Computers, IEEE Transactions on, vol.100, no.6, pp.623-629, 1971.
[17] James F Blinn. "Models of light reflection for computer synthesized pictures." ACM SIGGRAPH Computer Graphics ACM, vol.11, no. 2, 1977.
[18] Robert L. Cook, and Kenneth E. Torrance. "A reflectance model for computer graphics." ACM Transactions on Graphics (TOG), vol.1, no.1, pp.7-24, 1982.






































