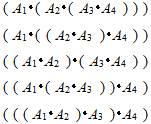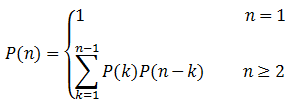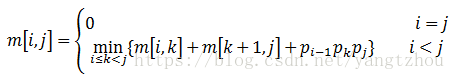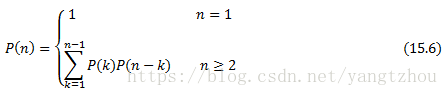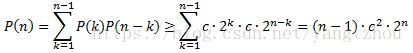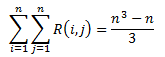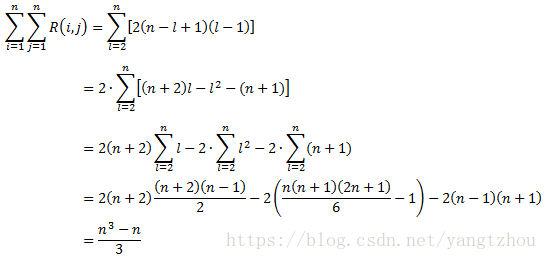算法导论 — 15.2 矩阵链乘法

笔记

       本节给出了一个关于矩阵链相乘问题的动态规划算法。给定一个n个矩阵的矩阵链，要计算它们的乘积。矩阵乘法满足结合律，所以通过加括号，一个矩阵链的乘法可以按照不同的顺序进行。例如，4个矩阵的矩阵链，共有5种加括号的方式：

      

       加括号的方式对矩阵链乘法的时间代价产生巨大的影响。我们先来分析两个矩阵相乘的时间代价。下面的代码给出了两个矩阵相乘的标准算法。

       

       两个矩阵A和B只有相容，即A的列数等于B的行数时，才能相乘。如果A是 p×q 矩阵，B是 q×r 矩阵，那么乘积C是 p×r 矩阵。分析上面的代码，矩阵乘法的时间代价主要由最内层循环的标量乘法的次数决定，一共需要做 pqr 次标量乘法。

       现在考虑计算矩阵链乘法的时间代价。以3个矩阵为例， 它们的维数分别为10×100、100×5和5×50，有以下两种加括号的方式：

       (1)   按的顺序计算

       先计算，需要做10×100×5 = 5000次标量乘法，得到的结果矩阵的维度为10×5；再与相乘，需要做10×5×50 = 2500次标量乘法。总共需要做5000+2500 = 7500次标量乘法。

       (2)   按的顺序计算

       先计算，需要做100×5×50 = 25000次标量乘法，得到的结果矩阵的维度为100×50； 再与的结果相乘，需要做10×100×50 = 50000次标量乘法。总共需要做25000+50000 = 75000次标量乘法。

       可以看到，第(2)种计算顺序的时间代价是第(1)种顺序的10倍。

       矩阵链乘法问题：给定一个n个矩阵的矩阵链，矩阵的维度为 (1 ≤ i ≤ n)，求一个最优的加括号方案，使得计算矩阵乘积所需要的标量乘法次数最少。

       矩阵的维度为，的维度为，... ...。以此类推，矩阵的维度为。矩阵的维度可以构成一个n+1元的数组。以这个数组作为算法输入。

       令P(n)表示n个矩阵的矩阵链的所有加括号的方案的数量。当n =1时，由于只有一个矩阵，所以P(1) = 1。当n ≥ 2时，可以先将矩阵链划分为两个子链和，其中k = 1,2,…, n-1，对两个子链加括号又是规模更小的子问题，因此矩阵链乘法问题满足最优子结构。由此，我们可以得到

       可以证明，。显然，遍历所有加括号的方案，并不是一个明智的选择，这样的算法至少有一个指数增长的时间复杂度。现在我们用动态规划方法来求解这个问题。

       用m[i, j]示计算矩阵链所需标量乘法次数的最小值。如果i = j，矩阵链中只有一个矩阵，显然m[i, j] = 0。对于i < j 的情况，上文提到，可以先将矩阵链划分为两个子链和。左子链的乘积是一个矩阵，右子链的乘积是一个矩阵。假设两个子链的最优解已知，它们分别为m[i, k]和m[k+1, j ]，并且可以知道两个子链的结果相乘需要次标量乘法。于是，可以得到。

       矩阵链的划分点k可以取值i, i+1,…, j-1，我们需要检查k的所有可能的取值情况，并从中找到最优解。于是有

       我们已经确立了问题的最优子结构，现在要合理安排子问题的求解顺序。子问题的规模是用相应的子链中矩阵的个数来度量的。我们要计算m[i, j]，只依赖于更短的子链的求解结果。因此，我们可以按照长度递增的顺序求解矩阵链乘法问题。另外，还需要在求解过程中记录下每个子问题的最优解的分割点位置k。以下是代码。

       

       算法MATRIX-CHAIN-ORDER包含一个三层的嵌套循环，运行时间为。另外，该算法还需要的空间来保存数组m和s。

 

练习

15.2-1 对矩阵规模序列<5,10, 3, 12, 5, 50, 6>，求矩阵链最优加括号方案。

       解

       最优加括号方案为，所需要的标量乘法的次数为2010。

 

15.2-2 设计递归算法MATRIX-CHAIN-MULTIPLY(A, s,i, j)，实现矩阵链最优代价乘法计算的真正计算过程，其输入参数为矩阵序列，MATRIX-CHAIN-ORDER得到的表s，以及下标 i 和 j 。(初始调用应为MATRIX-CHAIN-MULTIPLY(A, s, 1, n) )。

       解

       假设已经有两个矩阵相乘的代码MATRIX-MULTIPLY(A, B)。

       

 

15.2-3 用代入法证明递归公式(15.6)的结果为。

       解

       我们要证明的是，这个式子给出了P(n)的渐近下界，它的严格的数学含义是：存在正常量c和，使得对所有，有。

       用数学归纳法来证明这个命题。我们取。现在要选取合适的c，使得命题能够成立。

       初始条件要取n = 1、2、3、4。下面对这4个初始条件逐个分析。

       当n = 1时，这时有P(1) = 1，只要取0 < c ≤ 1/2，就能满足。

       当n = 2时，这时有P(2) = P(1)·P(1)= 1，只要取0 < c ≤ 1/4，就能满足。

       当n = 3时，这时有P(3) = P(1)·P(2)+ P(2)·P(1) = 2，只要取0 < c ≤ 1/4，就能满足。

       当n =4时，这时有P(4)= P(1)·P(3) + P(2)·P(2) + P(3)·P(1) = 5，只要取0 < c ≤ 5/16，就能满足。

       综合上述4个初始条件下c的取值范围可以得到，只要取0 < c ≤ 1/4，就能使命题对4个初始条件都成立。

       现在考虑n ≥ 5的情况。假设命题对所有1 ~ n-1都成立。于是有

       由于，因此只要不等式成立，就能使成立。我们求解不等式，得到c ≥ 1/(n-1)。只要取c ≥ 1/(5-1) = 1/4，就能使c ≥ 1/(n-1)对所有n ≥ 5都成立。于是有

       上式表明，在归纳阶段，取c ≥ 1/4可以使得命题成立。

       综上所述，初始条件下要取0 < c ≤ 1/4才能让命题成立，而归纳阶段要取c ≥ 1/4才能让命题成立。因此，我们可以取c = 1/4，这时命题对所有情况都成立。

 

15.2-4 对输入链长度为n的矩阵链乘法问题，描述其子问题图：它包含多少个顶点？包含多少条边？这些边分别连接哪些顶点？

       略

 

15.2-5 令R(i, j)表示在一次调用MATRIX-CHAIN-ORDER过程中，计算其他表项时访问表项m[i,j]的次数。证明：

       解

       考虑计算长度为 l 的矩阵子链乘积。如果l = 1，计算m[i, i]不需要访问其他表项。因此l = 1的情况可以不用考虑。

       现在我们考虑l > 1的情况。我们要从位置k处拆分一个长度为 l 的矩阵子链，其中k = i, i+1,… , i+l-2。每一次拆分需要访问两个表项m[i, k]和m[k+1, i+l-1]各一次。而k的可能取值有l-1个，因此处理一个长度为 l 的矩阵子链需要访问其他表项的次数为2(l-1)。在一个总长为n的矩阵链中，长度为l的子链一共有n-l+1个。因此处理所有长度为 l 的矩阵子链需要访问其他表项的次数为2(n-l+1)(l-1)次表项。将l = 2, 3, …, n的所有情况综合起来，可以得到

 

15.2-6 证明：对n个元素的表达式进行完全括号化，恰好需要n-1对括号。

       解

       用数学归纳法来证明这个命题。初始条件为n = 1，不需要括号，因此n = 1时命题成立。

       现在考虑n > 1的情况。假设命题对所有1 ~ n-1个元素的表达式都成立。对于n个元素的表达式，可以在一个任意的位置k处将它拆分，k = 1, 2, …, n-1。拆分后，左半边子表达式有k个元素，对它进行完全括号化恰好需要k-1对括号；右半边子表达式有n-k个元素，对它进行完全括号化恰好需要n-k-1对括号。还需要一对括号将两个子表达式括起来，如下所示，才能实现对n个元素的表达式的完全括号化。

（完全括号化的左半边子表达式    完全括号化的右半边子表达式）

       因此，对一个n个元素的表达式进行完全括号化，需要(k-1) + (n-k-1)+ 1 = n-1对括号。命题得证。

 

       相关代码可以从github下载。

       https://github.com/yangtzhou2012/Introduction_to_Algorithms_3rd/tree/master/Chapter15/Section_15.2/MatrixChainOrder