傅里叶变换和小波变换：时间序列异常检测

时间序列的聚类是高维度聚类（每个时间点作为一个维度出现）。所以很少使用经典聚类方法比如KMEANS。

最简单的时间序列特征是时域上以不同时间单位聚合作为特征。比如30天数据以日为单位，生成30维特征。最简单的聚类方法是直接以每个零售商各维度的特征为vector，用Euclidean distance为距离聚类。

这种方法的缺点是不考虑时域信号的位移信息：比如两家零售商在不同日期出现异常激活信号，用简单的聚类方法并不能把这两种信号归类为一类。在零售商数量多并且信号波形有很大差异时，这种方法会造成类别过多或完全不能区分正常和异常信号。

同样基于时域特征的相似性分析方法如动态时间归正（dynamic time warping, DTW）可以弥补欧几里得距离的缺陷，消除时域位移的影响。但是所有基于时域的特征提取都有维度过高和数据稀疏的缺点。尤其当业务关注的时间单位在小时级甚至以下，时域的特征个数和稀疏度会增加计算难度和影响聚类效果。

另一种提取时间序列特征的方法是通过频域变换，提取时间序列在频域的特征。频域特征可以降低特征空间的维度，使特征更集中。由于数据是离散采样数据，一般采用离散傅里叶变换或离散小波变换。

参考

[1] 高维稀疏向量聚类的挑战
[2] 不同时域和频域特征提取方法对比

傅里叶变换

傅里叶变换可以将时域信号转化为频域信号。在频域里，可以对信号使用比时域更简单的运算，比如滤波。

数字信号处理中常用的离散傅里叶变换DFT，是在离散信号的基础上使用傅里叶变换：

任何复数序列 $\left\{x_n\right\}:=x_0,x_1,\cdots ,x_{N-1}$ 都可以通过公式：

$${\mathbf{X}}_{\mathbf{k}}=\sum _{n=0}^{N-1}{x}_n\cdot e^{-\frac{2\pi i}{N}kn}=\sum _{n=0}N-1x_n\cdot [cos(2\pi kn/N)-i\cdot sin(2\pi kn/N)](1)$$

转化为新的序列 $\left\{{\mathbf{X}}_{\mathbf{k}}\right\}:={\mathbf{X}}_0,{\mathbf{X}}_1,\cdots ,{\mathbf{X}}_{\mathbf{N}-1}$

其中公式（1）也可以表示成 $\mathbf{X}=\mathcal{F}\left\{x\right\}$。

形象地说，DFT相当于把时域信号中的频率信息分别提取出来。

通常如果时域信号的频率特征不随时间变化而变化，可以使用DFT对时域信号作分解，经过滤波降噪后的信号（相当于降维）表示原始的时域信号。

对于在时域中有明显位置信息的信号波形（频域特征随时间有变化），采用傅里叶变换并不能识别时域的位置信息，造成提取后的特征信息丢失。

参考
[3] 傅里叶变换
[4] 图片来源

小波变换

另一种将时域信号转换为频域信号提取特征的方法是小波变换（wavelet transform）。选取小波变换而非傅里叶变换的主要原因是小波变换的基小波在时域有衰减，可以更好保留时域的位置信息，反映频域随时间的变化。

$$f(t)=\frac{1}{\sqrt{M}}\sum _k{W}_{\varphi }(0,k){\varphi }_{0,k}(t)+\frac{1}{\sqrt{M}}\sum _{j=0}^{\infty }\sum _k{W}_{\psi }(j,k){\psi }_{j,k}(t)(2)$$

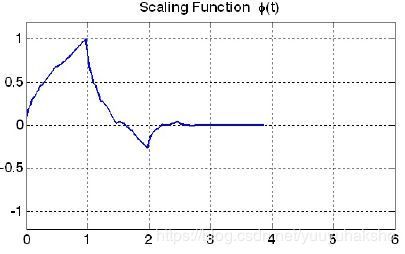
其中 $f(t)$为原始时域信号，${\varphi }_{0,k}(t)$ 是位置偏移量为k的尺度函数（scaling function），${\psi }_{j,k}(t)$是位置偏移量为k，尺度阶数（level）为j的小波函数（wavelet function），并且有：

$${\varphi }_{j,k}(t)=2^{j/2}\varphi (2^{j}t-k)(3)$$
$${\psi }_{j,k}(t)=2^{j/2}\psi (2^{j}t-k)(4)$$

公式（2）中的系数 $W_{\varphi }(0,k)$为近似系数（approximation coefficient），${\sum }_k{W}_{\varphi }(0,k){\varphi }_{0,k}(t)$ 项表示低通降噪后的平滑近似波形。

$W_{\psi }(j,k)$为小波系数 （detail coefficient），${\sum }_k{W}_{\psi }(j,k){\psi }_{j,k}(t)$项是各阶j上的高通滤波；各阶j的高通滤波器叠加用来表示波形中不同程度的变化。

紧支撑二进小波

在系数的表达上，为了避免系数增维的现象（即原始信号f(t)变为$W_{\varphi }(j,k)$和$W_{\psi }(j,k)$后由一维信息 t 变为 j 和 k 两维信息），采用紧支撑（compact support）二进（dyadic）小波函数的表达：

$${\psi }_n(t)=2^{j/2}\psi (2^{j}t-k)(5)$$

其中 $n=2^j+k$，j是满足$2^j\le n$的最大整数，紧支撑的区间取值限制在 $a\le 2^{j}t-k\le b$，对时域信号的分解变为：

$$f(t)=c_0\varphi (t)+\sum _{n=a}^b{c}_n{\psi }_n(t)(6)$$

多分辨率分析

这种时域信号f(t)的分解方式实际上是一种多分辨率分析（multi-resolution analysis，MRA）：将信号带宽分为高通high pass（或带通band pass）和低通low pass部分，然后根据分辨率需要持续迭代对低通部分进行等分（dyadic），每次保留带通的滤波结果。

随n的增大，尺度阶数j增大，时域函数越窄，频域带宽加倍。当等分到频率不能继续分割时，剩下的低频部分由低通滤波器表示（即尺度函数），防止出现无穷长的小波系数。

MRA在计算上有一种快速的鱼骨算法（因为对低通部分的等分过程可视化后像一条鱼骨）。鱼骨算法的本质是迭代求解f(t)分解公式中的近似系数和小波系数，它的基础是相邻尺度 j 和 j+1 内的scaling function的迭代关系：

因为尺度 j 内的scaling function 就是尺度 j+1内的scaling function经低通滤波后的结果，同理尺度 j 内的wavelet function就是尺度 j+1 内的scaling function经带通滤波后的结果，所以有尺度 j 内的scaling function：

$$\varphi (2^{j}t)=\sum _k{h}_{j+1}(k)\varphi (2^{j+1}t-k)(7)$$

尺度 j 内的wavelet function（也来自相邻尺度内的scaling function）：

$$\psi (2^{j}t)=\sum _k{g}_{j+1}(k)\varphi (2^{j+1}t-k)(8)$$

称为双尺度关系（two-scale relation）或多分辨率公式（multi-resolution formulation）。其中$h_j(k)$是一个低通滤波器，$g_j(k)$是一个高通滤波器。在离散数字信号中，这两个滤波器h(k)和g(k)是与 t 无关的固定的离散数列，并且可以迭代推导出近似系数$W_{\varphi }(j,k)$和小波系数$W_{\psi }(j,k)$的公式：

$$W_{\varphi }(j-1,k)=\sum _{m}h(m-2k)W_{\varphi }(j,k)(9)$$

$$W_{\psi }(j-1,k)=\sum _{m}g(m-2k)W_{\varphi }(j,k)(10)$$

数列 h(k)又称为尺度向量（scaling factor）。公式(9)和(10)相当于对上一个尺度下的系数的间隔采样。

如果可以提前获取固定数列h(k)和g(k)，即使没有显式的尺度函数和小波函数，也可以快速计算各个尺度的近似系数和小波系数。

尺度函数的构造

以项目中用到的Daubechies系列波形db2为例：

尺度向量 h(k)值为

$$h(0)=\frac{1+\sqrt{3}}{4},h(1)=\frac{3+\sqrt{3}}{4},h(2)=\frac{3-\sqrt{3}}{4},h(3)=\frac{1-\sqrt{3}}{4}$$

对应构造的尺度函数scaling function：

尺度函数满足：

1. 标准性 normalization：$\int \varphi (x)\mathrm{d}x=1$
2. 正交性 orthogonality：$\int \varphi (x-k)\varphi (x-l)\mathrm{d}x={\delta }_{k,l}$，其中${\delta }_{k,l}$是Kronecker delta.
3. 尺度关系 scaling relation $\varphi (x)={\sum }_{k}h(k)\varphi (2x-k)$

小波系数 $g(k)=(-1{)}^{k}h(-k+1)$。

基本小波（basis wavelet function）$\psi(t) = $

小波函数wavelet function：

参考

[5] 小波变换
[6] 小波分析和尺度函数
[7] 紧支撑正交小波的构造

离散小波变换参数选择

1 尺度向量h(k)的长度N：

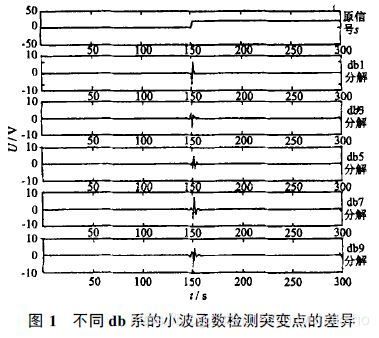
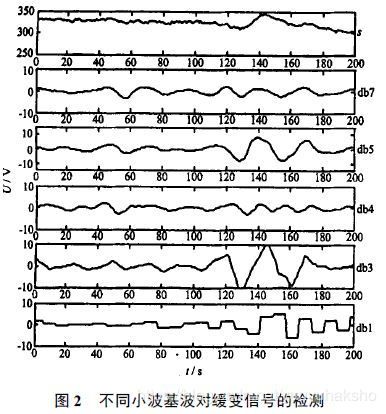
N也代表消失矩（vanishing moment），是低通滤波器平滑程度的指数。N越大，低通滤波器越平滑，带通滤波器震荡性越强；时域上的紧支撑性会变差（时域特征分辨率下降），同时频域上的紧支撑性会变强（频域特征分辨率增加）。这会造成对时域阶跃信号的识别困难，但更容易拟合时域的平滑信号。同时更大的N也会造成更大的计算量。

以Daubechies系列小波的阶数为例：dbX的基小波实际h(k)长度为2X，所以db2的h(k)有4个值。项目中同时采用了低阶和高阶的db系列基小波，同时拟合突变和渐变信号并确保对时域和频域信息的分辨率。

对比db系列不同滤波长度对突变和渐变信号的模拟效果：

来源：故障信号检测的小波基选择方法

2 尺度 j 的选择：

根据紧支撑二进小波的定义，尺度j的最大值为 $j_{max}=int(lo{g}_2(\frac{n}{N}-1)$，其中 n 为时域信号长度，N为所选基小波滤波器长度。

在此范围内，根据多分辨率分析方法：随 j 增大，各尺度的带宽会变窄，对频域特征的分辨率会增强，同样也会造成对时域阶跃信号的识别困难和对时域平滑信号的更好拟合。

代码实现

level代表尺度 j，wavelet代表基小波dbX，滤波长度为N=2X。

mode = 'zero’定义了时域信号开始和结束位置的padding方式为添加0。其他可能的padding方式包括循环、镜像、etc.

如果output选择’all’，则特征包含近似系数和小波系数。如果选择‘cA_only’，则只提取近似系数。

def getDwtCoefs(ts, mode='zero',level=[], wavelet = ['db2','db4','db10'],
                output='cA_only'):
    '''
    1-dimension single level DWT: returned coeficients interpretation:
        cA: approximation coefs, or low pass filter
        cD: detail coefs, or high pass filter
    1-dimension multi-level DWT: returns cA_n, cD_n, cD_{n-1}, ... cD_1
    for quick reference: 
        http://eeweb.poly.edu/iselesni/pubs/WaveletQuickStudy_expanded.pdf
    '''
    if len(level) < len(wavelet):
        level = np.ones(len(wavelet), dtype=int)
    level = [int(x) for x in level]
    
    result = []
    coefs_all = []
    for w,l in zip(wavelet,level):
        try:
            coefs = pywt.wavedecn(ts, w, mode=mode, level=l)
            if output == 'all':
                arr, _ = pywt.coeffs_to_array(coefs)
                result = result + arr.tolist()
            elif output == 'cA_only':
                result += coefs[0].tolist()
            else: 
                result += coefs[0].tolist()
                
            coefs_all.append(coefs)
            
        except ValueError:
            print(len(ts), w, l)
            print(traceback.format_exc())
    
    return result, coefs_all

def getStats(row):
    return [np.sum(row), np.mean(row), np.max(row), np.std(row)]

def runDWT(data, oneHotColn, wavelet, mode, timeUnit, time_resolution,
           onlyNightShift=True):
    # calculate maximum DWT level
    if onlyNightShift is True:
        dataLen = int(len(timeUnit) / 3)
    else:
        dataLen = int(len(timeUnit) / 3 * 2)
    level = []
    for w in wavelet:
        # dwt_max_level(input timeseries size, nr. coefficients for the specified decomposition order)
        # returns maximum allowed level for the chosen daubechies order
        wt = pywt.Wavelet(w)
        level.append(pywt._multilevel.dwt_max_level(dataLen, wt.dec_len))
        level = [np.min([x,4]) for x in level]
    
    newTs = []
    originalTs = []
    statsTs = []
    for idx, col in enumerate(oneHotColn):
        ts = np.array(data.loc[:,data.columns.isin([time_resolution, col])].groupby(
            time_resolution).agg({col: 'sum'})).flatten()
        statsTs.append(getStats(ts))
        
        if onlyNightShift is True:
            ts = [x for x,y in zip(ts,timeUnit) if int(y.hour)<8]
        else:
            # only day shifts:
            ts = [x for x,y in zip(ts,timeUnit) if int(y.hour)>=8]
        
        originalTs.append(ts)
        result, coefs_all = getDwtCoefs(ts, level=level, wavelet=wavelet, 
                                             mode=mode)
        newTs.append(result)
        
    tsTbl_original = pd.DataFrame(originalTs, index=oneHotColn)
    tsTbl_stats = pd.DataFrame(statsTs, columns=['rowSum','rowMean',
                                    'rowMax','rowStd'], index=oneHotColn)
    tsTbl_original['label'] = '-1'
    tsTbl_coefs = pd.DataFrame(newTs, index=oneHotColn)
    
    return tsTbl_original, tsTbl_coefs, tsTbl_stats