粒子群算法

第二篇博客，为大家简单介绍粒子群算法（PSO）基本原理。

粒子群算法同遗传算法相似，也是根据生物界中的种群行为而发明的一种算法。也是解决优化问题常用的一种算法。其原理简单，实现起来也不复杂，并且经过自己编程实践发现其速度要优于遗传算法。

粒子群算法源于鸟群觅食行为，假设有一群鸟，在随机搜索食物，在搜索区域内只有一块儿食物，一开始时所有的鸟儿都不知道食物所在的方位，但它们能够知道自己离食物有多远，以及它们能够记住在自己飞过的路程当中距离食物最近的位置，同时它们也能够知道鸟群中所有鸟儿经过的路程当中，离食物最近的位置。那每一只鸟儿将如何去寻找食物呢？简单来说，每一只鸟儿在当前位置的基础上，如何做出决策，下一步向哪里飞呢？实际，每只鸟儿将综合自身的经验，以及群体的经验来在做出下一步飞向哪里的决策，即每只鸟儿将根据自己所经过的路程中离食物最近的位置以及鸟群中所有鸟儿经过的路程当中离食物最近的位置来做出决策，决定下一步自己向哪里飞。这便是粒子群算法的基本原理

在粒子群算法中，粒子的位置对应于原问题的解。粒子的适应值就是将粒子的位置（对应于原问题的解）带入到目标函数中所得到的目标函数值。粒子的速度决定粒子下一步向哪里飞以及飞多远。

接下来先给在粒子群算法中最重要的两个公式：

在给出公式之前，先设定一些符号，

：代表优化问题在D维空间上的一个解，对应于粒子群中第i个粒子的位置

：代表第i个粒子所经历的所有路程上最优的位置，即其在飞翔过程中离目标函数最优解最近的位置

：代表所有粒子经历过的路程上的最优位置（可以认为是所有个体最优位置当中的最优位置）

：代表粒子i的飞翔速度

好了，接下来给出两个粒子群算法中的核心公式

公式一：

公式二：

在上面两个公式中，代表粒子编号；代表维度编号；为惯性因子，其取值范围为非负；为加速常数，其取值范围为非负常数；为0到1范围内的随机数；为约束因子，用来控制速度的权重。

需要说明的是，为了限制某个粒子的飞翔范围过大，我们为粒子的每一个维度设置一个最大飞翔速度，即如果粒子i在d维上的飞翔速度大于，则将这一维上的飞翔速度设置为，如果小于则将其设置为。的取值一般为对应维度所代表的决策变量取值范围的百分之十到百分之二十。例如设决策变量的取值范围为，则。

接下来对上文中的一些参数加以解释说明：

1.粒子数：粒子数的选取一般在20个到40个之间，但是需要具体问题具体对待，如果对于复杂问题，则需要设置更多的粒子，粒子数量越多，其搜索范围就越大。

2.惯性因子：用来控制继承多少粒子当前的速度的，越大则对于当前速度的继承程度越小，越小则对于当前速度的继承程度越大。有些同学可能会产生疑问，是不是说反了。其实不是，从公式中可以明确看出，其值越大，则速度的改变幅度就越大，则对于粒子的当前速度继承越小；反之，速度的改变幅度越小，则对于粒子当前速度继承越大。因此如果的值越大，则解的搜索范围越大，可以提高算法的全局搜索能力，但也损失了局部搜索能力，有可能错失最优解；反之如果的值越小，则解的搜索范围也就越小，算法的全局搜索能力也就越小，容易陷入局部最优。如果是变量，则其值应该随着迭代次数的增加而减小（类似于梯度下降当中的学习率）。如果为定值，则建议在0.6到0.75之间进行选取。

3.加速常数：通过公式一可以看出，加速常数控制着飞翔速度的计算是更加看重自身经验还是群体经验。公式一中的第二项就是自身经验的体现，加速常数可以看做是用来调整自身经验在计算粒子飞翔速度上的权重。同理是用来控制群体经验在计算粒子飞翔速度过程中的权重的。如果为0，则自身经验对于速度的计算不起作用，如果为0，则群体经验对于粒子飞翔速度的计算不起作用。的取值在学术界分歧很大主要有如下几种情况：

学者	和
Clerc
Carlisle
Trelea
Eberhart

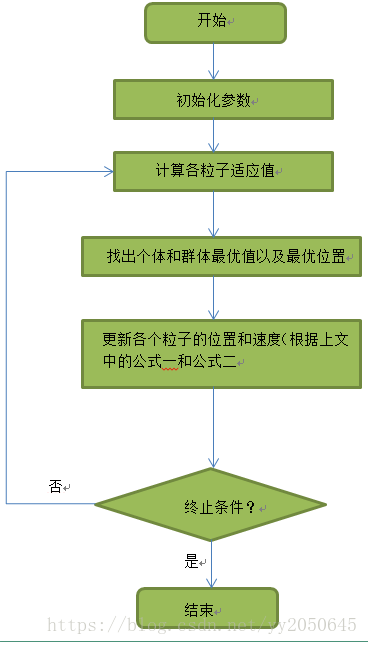
以下为粒子群算法的具体流程：

此处需要注意的是，如果为每一个决策变量设置了取值范围，为了限制每一次求取的个体最优位置（原问题的解）的每一维在设定的取值范围之内，可以对每一次迭代获得的粒子的位置进行以下设定：如果某个粒子的位置在更新后，某一维超出了设定的决策变量的取值范围，则如果原问题为最大化问题，则设定这个粒子的适应度为负无穷，如果原问题为最小化问题，则设定这个粒子对应的适应度为正无穷，经过这样设置之后，这个粒子的位置一定不会成为个体最优位置，因此更不可能成为群体最优位置。这样，就起到了对于在范围之外的解的剔除的作用（这也是我在程序中所采取的方案）。举个例子：例如求取的最小值，如果不进行上述设置，可能会求得最优解为，对此，我们只需要设定不符合取值范围的解的适应度均为正无穷即可。

以上便是本人对于粒子群算法的粗浅理解，希望可以帮助到大家，如有不足之处请多多包涵，同时也欢迎大家给出宝贵的意见，共同学习，共同进步。

以下附上本人使用python编写的关于粒子群算法的程序：

import numpy as np
import time
from numpy import random as rd
import matplotlib.pyplot as plt
np.set_printoptions(linewidth=1000, suppress=True)


def objective_func(x, y):
    # 这是一个用来测试的目标函数
    return 2 * np.pi * np.exp(-0.2 * ((x ** 2 + y ** 2) / 2) ** 0.5) + np.exp(0.5 * (np.cos(2 * np.pi * x) + np.cos(2 * np.pi * y))) - 2 * np.pi


def objective_func2(x):
    # 这也是一个用来测试的目标函数
    return x ** 2


def GetTime(func_name):
    def wrapper(*args, **kwargs):
        start_time = time.time()
        ret = func_name(*args, **kwargs)
        end_time = time.time()
        run_time = end_time - start_time
        print("pso算法运行时间为%f秒" % run_time)
        return ret
    return wrapper


class PSO(object):

    def __init__(self, alpha, times, obj_type, particle_num, w, c1, c2, obj_func, **kwargs):
        """

        :param alpha: 约束因子，用来控制速度的权重
        :param times: 算法的迭代次数
        :param obj_type: 目标函数的类型，传入"Max"表示目标函数为最大化问题，传入"Min"表示目标函数为最小化问题
        :param particle_num: 粒子数量
        :param w: 惯性因子
        :param c1: 加速常数
        :param c2: 加速常数
        :param obj_func: 被优化的目标函数
        :param kwargs: 目标函数决策变量及取值范围，给定方式例如：x1=(x1_min, x1_max), x2=(x2_min, x2_max), ...,
                        注意此处决策变量及其范围给定的顺序需和目标函数obj_func中决策变量参数顺序一致
        """
        self.alpha = alpha
        self.times = times
        self.obj_type = obj_type
        self.particle_num = particle_num
        self.w = w
        self.c1 = c1
        self.c2 = c2
        self.obj_func = obj_func
        self.kwargs = kwargs
        # self.v_max确定决策变量每一维的最大飞翔速度，根据最大飞翔速度为决策变量取值范围的百分之10到百分之20之间来取值
        self.v_max = (np.array(list(kwargs.values()))[:, 1] - np.array(list(kwargs.values()))[:, 0]) * 0.15
        assert np.all(self.v_max > 0), "输入决策变量的最小值大于最大值"
        self.particles = np.empty((self.particle_num, len(self.kwargs)))
        # for循环初始化初代粒子群
        for dimension in range(len(self.kwargs)):
            var_range = list(self.kwargs.values())[dimension]
            self.particles[:, dimension:dimension + 1] = rd.uniform(var_range[0], var_range[1], (self.particle_num, 1))
        assert self.obj_type.lower() in ["max", "min"], "目标函数类型填写错误, 请填写'Max'或'Min'"
        if self.obj_type.lower() == "max":
            self.individual_best_fit_value = [-float("inf")] * self.particle_num
        else:
            self.individual_best_fit_value = [float("inf")] * self.particle_num
        self.individual_best_fit_value = np.array(self.individual_best_fit_value)
        self.individual_best_position = np.empty((self.particle_num, len(self.kwargs)))
        # 确定初始速度
        self.v = np.array([rd.uniform(-v_max_value, v_max_value, self.particle_num) for v_max_value in self.v_max]).T
        # self.bests_pop_fit_values用于存放每次迭代群体最优适应度, self.bests_pop_positions用于存放每次迭代最优群体适应度对应的位置
        self.bests_pop_fit_values = []
        self.bests_pop_positions = []

    def get_fit_value(self):
        # 求取每个粒子的适应度
        self.fit_value = np.empty(self.particle_num)
        for particle_index in range(self.particle_num):
            decision_var = self.particles[particle_index]
            decision_var_max = np.array(list(self.kwargs.values()))[:, 1]
            decision_var_min = np.array(list(self.kwargs.values()))[:, 0]
            # 一下用于限制决策变量在设定的取值范围之内，如果出了取值范围则设置其适应度为负无穷或正无穷
            if np.all((decision_var_max - decision_var) >= 0) and np.all((decision_var - decision_var_min) > 0):
                self.fit_value[particle_index] = self.obj_func(*tuple(self.particles[particle_index]))
            else:
                if self.obj_type.lower() == "max":
                    self.fit_value[particle_index] = -float("inf")
                else:
                    self.fit_value[particle_index] = float("inf")

    def get_best(self):
        # 获取个体最优以及群体最优粒子位置
        # replace_index为个体最优位置需要替换的粒子的索引
        if self.obj_type.lower() == "max":
            replace_index = self.fit_value > self.individual_best_fit_value
        else:
            replace_index = self.fit_value < self.individual_best_fit_value
        self.individual_best_position[replace_index] = self.particles[replace_index]
        self.individual_best_fit_value[replace_index] = self.fit_value[replace_index]
        # 根据个体最优适应度获得群体最优适应度，以及群体最优粒子位置
        if self.obj_type.lower() == "max":
            self.pop_bset_fit_value = np.max(self.individual_best_fit_value)
        else:
            self.pop_bset_fit_value = np.min(self.individual_best_fit_value)
        best_index = list(self.individual_best_fit_value).index(self.pop_bset_fit_value)
        self.pop_best_position = self.individual_best_position[best_index]
        self.bests_pop_fit_values.append(self.pop_bset_fit_value)
        self.bests_pop_positions.append(self.pop_best_position)

    def calc_v_position(self):
        # 得到粒子群移动后的位置
        self.v = self.v + self.c1 * rd.random() * (self.individual_best_position - self.particles) + self.c2 * rd.random() * (self.pop_best_position - self.particles)
        # 以下两步用于限制速度在[-self.v_max, self.v_max]之内
        self.v = np.array([self.v[r, c] if self.v[r, c] < self.v_max[c] else self.v_max[c] for r in range(self.particle_num) for c in range(len(self.kwargs))]).reshape(self.particle_num, len(self.kwargs))
        self.v = np.array([self.v[r, c] if self.v[r, c] > -self.v_max[c] else -self.v_max[c] for r in range(self.particle_num) for c in range(len(self.kwargs))]).reshape(self.particle_num, len(self.kwargs))
        # 根据计算出的速度获取粒子群移动后的位置
        self.particles = self.particles + self.alpha * self.v

    @GetTime
    def run(self):
        for i in range(self.times):
            self.get_fit_value()
            self.get_best()
            self.calc_v_position()
        print("目标函数最优值为：", self.bests_pop_fit_values[-1])
        print("最优解为：", self.bests_pop_positions[-1])
        self.draw()

    def draw(self):
        fig = plt.figure()
        ax = plt.subplot(1, 1, 1)
        ax.plot(np.arange(1, self.times + 1), self.bests_pop_fit_values, label="fit_value trend", color="r")
        ax.set_xlabel("iterate times")
        ax.set_ylabel("fit_value")
        ax.grid()
        ax.legend()
        ax.set_title("PSO")
        plt.show()


def main():
    pso = PSO(0.8, 400, "Min", 50, 0.2, 2, 2, objective_func2, x1=(-30, 30))
    pso.run()
    pso = PSO(0.8, 400, "Max", 50, 0.2, 2, 2, objective_func, x1=(-30, 30), x2=(-30, 30))
    pso.run()


if __name__ == "__main__":
    main()