自学习策略和Lévy飞行的正弦余弦优化算法
文章目录
- 一、理论基础
-
- 1、正弦余弦优化算法
- 2、改进的正弦余弦优化算法
-
- (1)自学习策略
- (2)停滞扰动策略
- (3)SCASL寻优步骤
- 二、仿真结果及分析
- 三、参考文献
一、理论基础
1、正弦余弦优化算法
请参考这里。
2、改进的正弦余弦优化算法
(1)自学习策略
受粒子群算法中惯性权重控制参数启发,引入非线性调整参数 ω \omega ω用于调节种群迭代过程中搜索个体对当前自身位置信息的依赖,以提高算法的全局搜索能力。迭代前期,搜索个体的位置更新应低程度地依赖自身位置信息,以便于搜索更大的空间,提高算法的全局搜索能力;迭代后期应高程度地依赖自身位置信息与当前最优解位置信息,以提高算法的收敛速度,得到全局最优解。非线性调整参数 ω \omega ω更新公式为 ω = ( t / t max ) 2 (1) \omega=(t/t_{\max})^2\tag{1} ω=(t/tmax)2(1)此外,针对种群迭代过程中只依赖于当前种群最优解易于陷入局部最优的缺陷,对比粒子群算法中“自学习环节”和“社会学习环节”,SCA种群更新模型中只包含“社会学习环节”,研究在每次迭代过程中将每个个体搜索到的历史最优解保存下来,引入“自学习环节”提高种群多样性,避免陷入局部最优,改进算法的搜索性能。引入非线性权重因子和“自学习环节”后的搜索个体位置更新公式为 X i t + 1 = { ω ⋅ X i t + r 1 ⋅ sin ( r 2 ) ⋅ ( ∣ X ∗ − X i t ∣ + ∣ X i ∗ − X i t ∣ ) , r 4 < 0.5 ω ⋅ X i t + r 1 ⋅ cos ( r 2 ) ⋅ ( ∣ X ∗ − X i t ∣ + ∣ X i ∗ − X i t ∣ ) , r 4 ≥ 0.5 (2) X_i^{t+1}=\begin{dcases}\omega\cdot X_i^t+r_1\cdot\sin(r_2)\cdot(|X^*-X_i^t|+|X_i^*-X_i^t|),\quad r_4<0.5\\\omega\cdot X_i^t+r_1\cdot\cos(r_2)\cdot(|X^*-X_i^t|+|X_i^*-X_i^t|),\quad r_4≥0.5\end{dcases}\tag{2} Xit+1={ω⋅Xit+r1⋅sin(r2)⋅(∣X∗−Xit∣+∣Xi∗−Xit∣),r4<0.5ω⋅Xit+r1⋅cos(r2)⋅(∣X∗−Xit∣+∣Xi∗−Xit∣),r4≥0.5(2)其中, X i ∗ X_i^* Xi∗为第 i i i个搜索个体搜索到的历史最优位置。
(2)停滞扰动策略
Lévy飞行的特点为长时间以较小步长随机游走,偶尔以较大步长进行方向突变跳跃,与智能优化算法中的全局搜索和局部搜索特征相似。因此,Lévy飞行被研究人员广泛应用在各种优化算法中,用于产生随机步长,在种群搜索个体更新过程中施加一个扰动量,丰富种群多样性,提高算法的搜索能力。Lévy飞行的数学模型请参考这里。
易于陷入局部最优,出现早熟收敛现象是大多数智能优化算法所面临的问题,SCA由于其架构特点更是如此。随着寻优过程中迭代次数的增加,当种群所有个体搜索到的历史最优个体的适应度值均值连续5次迭代不再变化,则认为搜索陷入停滞,此时采用Lévy飞行随机游走策略更新种群搜索个体的位置,提高种群多样性,使算法跳出局部最优。基于Lévy飞行的停滞扰动策略模型为 X i t + 1 = X ∗ + randn ⋅ Levy ( X i ) + randn ⋅ ∣ X i ∗ − X i t ∣ (3) X_i^{t+1}=X^*+\text{randn}\cdot\text{Levy}(X_i)+\text{randn}\cdot|X_i^*-X_i^t|\tag{3} Xit+1=X∗+randn⋅Levy(Xi)+randn⋅∣Xi∗−Xit∣(3) Levy ( X i ) = α ⋅ s ⋅ ( X ∗ − X i t ) (4) \text{Levy}(X_i)=\alpha\cdot s\cdot(X^*-X_i^t)\tag{4} Levy(Xi)=α⋅s⋅(X∗−Xit)(4)其中, randn \text{randn} randn为服从正态分布的随机量; α ∈ [ − 1 , 1 ] \alpha\in[-1,1] α∈[−1,1]为比例因子。
(3)SCASL寻优步骤
算法:自学习策略和Lévy飞行的正弦余弦算法
Step 1:设置算法的基本参数:种群数目 N N N,最大迭代次数 t max t_{\max} tmax,问题维度 D D D,比例因子 α \alpha α,Lévy飞行指数参数 β \beta β;
Step 2:随机初始化初始种群搜索个体在搜索空间的位置信息,并进行边界控制;
Step 3:计算每个个体的适应度值,更新当前搜索到的最优个体位置信息以及每个搜索个体搜索到的历史最优位置信息;
Step 4:判断搜索是否陷入停滞,如果停滞,执行Step 5;否则,执行Step 6;
Step 5:采用停滞扰动策略更新种群搜索个体的位置,执行Step 7;
Step 6:更新控制参数 r 1 , r 2 , r 4 , ω r_1,r_2,r_4,\omega r1,r2,r4,ω,采用式(2)更新种群搜索个体的位置;
Step 7:对新个体位置进行边界控制,对越界值进行随机初始化;
Step 8:计算每个个体的适应度值,更新当前搜索到的最优个体位置信息以及每个搜索个体搜索到的历史最优位置信息;
Step 9:判断是否满足算法结束条件,不满足,则执行Step 4;否则,输出得到的最优值,算法寻优结束。
二、仿真结果及分析
为了检验所提出SCASL的性能,将其与基本SCA和3个性能较优的智能优化算法SSA、WOA、GSA进行对比,以文献[1]中表1的F1、F2、F3、F5、F8、F13为例。所有算法最大迭代次数均设为500,种群规模均设为30,函数维数均为30,每个算法独立运行30次,结果显示如下:

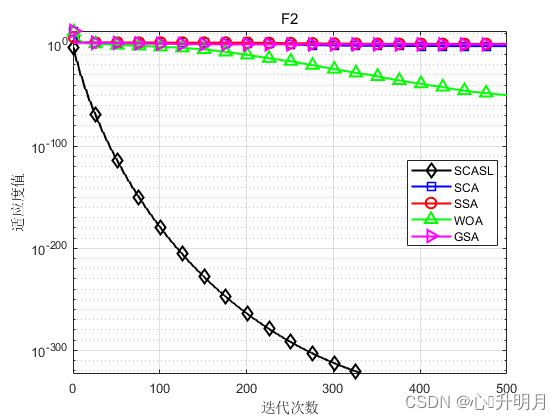
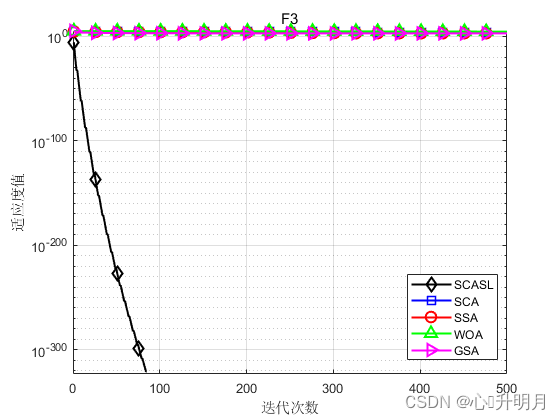


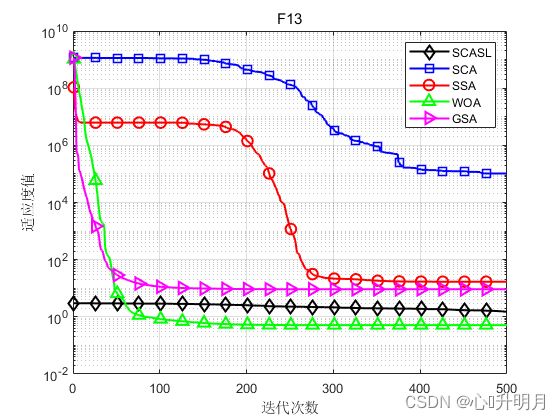
函数:F1
SCASL:最差值: 0,最优值: 0,平均值: 0,标准差: 0,秩和检验: NaN
SCA:最差值: 248.5974,最优值: 0.11683,平均值: 24.0009,标准差: 54.9918,秩和检验: 1.2118e-12
SSA:最差值: 4.502e-07,最优值: 3.0122e-08,平均值: 1.2159e-07,标准差: 9.4925e-08,秩和检验: 1.2118e-12
WOA:最差值: 2.1096e-71,最优值: 1.8647e-88,平均值: 7.2339e-73,标准差: 3.849e-72,秩和检验: 1.2118e-12
GSA:最差值: 1.6178,最优值: 8.8316e-17,平均值: 0.05842,标准差: 0.29554,秩和检验: 1.2118e-12
函数:F2
SCASL:最差值: 0,最优值: 0,平均值: 0,标准差: 0,秩和检验: NaN
SCA:最差值: 0.094198,最优值: 0.00038808,平均值: 0.013099,标准差: 0.019587,秩和检验: 1.2118e-12
SSA:最差值: 4.9295,最优值: 0.11254,平均值: 2.0862,标准差: 1.3905,秩和检验: 1.2118e-12
WOA:最差值: 7.766e-50,最优值: 6.8314e-59,平均值: 4.4822e-51,标准差: 1.5535e-50,秩和检验: 1.2118e-12
GSA:最差值: 4.8503,最优值: 4.8122e-08,平均值: 0.6082,标准差: 1.3029,秩和检验: 1.2118e-12
函数:F3
SCASL:最差值: 0,最优值: 0,平均值: 0,标准差: 0,秩和检验: NaN
SCA:最差值: 23404.9896,最优值: 943.858,平均值: 7785.1583,标准差: 5232.5829,秩和检验: 1.2118e-12
SSA:最差值: 3324.9494,最优值: 344.1169,平均值: 1176.2633,标准差: 642.5721,秩和检验: 1.2118e-12
WOA:最差值: 80057.958,最优值: 4230.3131,平均值: 41798.3283,标准差: 14150.264,秩和检验: 1.2118e-12
GSA:最差值: 1481.4396,最优值: 375.46,平均值: 844.4256,标准差: 279.9404,秩和检验: 1.2118e-12
函数:F5
SCASL:最差值: 28.9457,最优值: 28.3496,平均值: 28.7308,标准差: 0.17682,秩和检验: 1
SCA:最差值: 436477.0862,最优值: 166.8729,平均值: 48480.8381,标准差: 94200.9352,秩和检验: 3.0199e-11
SSA:最差值: 2042.3595,最优值: 27.5572,平均值: 313.1004,标准差: 488.2802,秩和检验: 8.4848e-09
WOA:最差值: 28.7609,最优值: 27.2042,平均值: 28.1214,标准差: 0.41328,秩和检验: 6.0104e-08
GSA:最差值: 401.884,最优值: 25.2817,平均值: 75.7753,标准差: 92.9514,秩和检验: 0.14945
函数:F8
SCASL:最差值: -5603.8967,最优值: -8627.4624,平均值: -6806.0638,标准差: 617.4353,秩和检验: 1
SCA:最差值: -3365.3783,最优值: -4437.8936,平均值: -3776.9122,标准差: 253.2758,秩和检验: 3.0199e-11
SSA:最差值: -5237.1885,最优值: -9071.6193,平均值: -7518.3567,标准差: 809.0847,秩和检验: 0.00023885
WOA:最差值: -7440.2863,最优值: -12568.2503,平均值: -9961.0152,标准差: 1663.0295,秩和检验: 7.3891e-11
GSA:最差值: -1705.9147,最优值: -3671.81,平均值: -2592.2496,标准差: 509.7123,秩和检验: 3.0199e-11
函数:F13
SCASL:最差值: 2.1991,最优值: 0.97953,平均值: 1.5176,标准差: 0.34378,秩和检验: 1
SCA:最差值: 1567425.596,最优值: 4.218,平均值: 103183.3736,标准差: 308135.025,秩和检验: 3.0199e-11
SSA:最差值: 53.6636,最优值: 0.017279,平均值: 16.9143,标准差: 15.3019,秩和检验: 4.3531e-05
WOA:最差值: 1.1686,最优值: 0.077865,平均值: 0.51484,标准差: 0.25684,秩和检验: 4.5043e-11
GSA:最差值: 22.6902,最优值: 0.3912,平均值: 9.2077,标准差: 7.0328,秩和检验: 2.4913e-06
实验结果表明,SCASL相比标准SCA和较新的优化算法SSA、WOA、GSA,具有更高的计算效率、收敛精度以及更强的局部最优规避能力。
三、参考文献
[1] 李银通, 韩统, 赵辉, 等. 自学习策略和Lévy飞行的正弦余弦优化算法[J]. 重庆大学学报, 2019, 42(9): 55-65.