GAT - Graph Attention Network 图注意力网络 ICLR 2018
文章目录
- 1 相关介绍
- GCN的局限性
- 本文贡献(创新点)
- attention 引入目的
- 相关工作
- 谱方法 spectral approaches
- 非谱方法 non-spectral approaches (基于空间的方法)
- 注意力机制 self-attention
- 2 GAT
- 2.1 Graph Attentional Layer
- 计算注意力系数(attention coefficient)
- 加权求和(aggregate)
- multi-head attention机制
- 2.2 和当前工作的对比
- 3 实验和评价
- 数据集
- 半监督学习transductive learning
- 归纳学习inductive learning
- 4 总结
- GAT模型的特点
- GAT模型的局限及未来的研究方向
- GAT核心公式
- GAT的DGL实现
- 参考
论文题目:Graph Attention Network (GAT)
时间:2018
来源:ICLR
论文链接:https://arxiv.org/abs/1710.10903
Github链接:https://github.com/Diego999/pyGAT
1 相关介绍
graph上的deep learning方法无外乎就是希望学习节点特征以及节点在图中的结构特征。
GCN的局限性
- 无法完成inductive任务,即处理动态图问题。inductive任务是指:训练阶段与测试阶段需要处理的graph不同。通常是训练阶段只是在子图(subgraph)上进行,测试阶段需要处理未知的顶点。(unseen node)
- 处理有向图的瓶颈,不容易实现分配不同的学习权重给不同的neighbor
- 对于一个图结构训练好的模型,不能运用于另一个图结构(所以此文称自己为半监督的方法)
本文贡献(创新点)
- 引入masked self-attentional layers 来改进前面图卷积的缺点
- 对不同的相邻节点分配相应的权重,既不需要矩阵运算,也不需要事先知道图结构
- 四个数据集上达到state-of-the-art的准确率Cora、Citeseer、Pubmed、protein interaction
attention 引入目的
- 为每个节点分配不同权重
- 关注那些作用比较大的节点,而忽视一些作用较小的节点
- 在处理局部信息的时候同时能够关注整体的信息,不是用来给参与计算的各个节点进行加权的,而是表示一个全局的信息并参与计算
相关工作
对待图结构的数据有两种方法,谱方法和非谱方法
谱方法 spectral approaches
例如:GCN
Semi-Supervised Classification with Graph Convolutional Networks,ICLR 2017这篇文章中的方法
解析 :Semi-Supervised Classification with Graph Convolutional Networks用图卷积进行半监督分类
非谱方法 non-spectral approaches (基于空间的方法)
例如:GraphSAGE
William L Hamilton, Rex Ying, and Jure Leskovec. Inductive representation learning on largegraphs. Neural Information Processing Systems (NIPS), 2017.
解析:GraphSAGE:Inductive Representation Learning on Large Graphs
这种方法是将相邻节点设置为固定的长度,然后进行specific aggregator,这种方法在几个大的benchmarks上取得了非常好的效果。
注意力机制 self-attention
优点:可以处理任意大小输入的问题,并且关注最具有影响能力的输入。
注意力机制再RNN与CNN之中,都取得了不错的效果,并且可以达到state-of-the-art的性能。
attention来源于自然语言处理领域的这篇很著名的文章:
Attention is all you need
2 GAT
2.1 Graph Attentional Layer
和所有的attention mechanism一样,GAT的计算也分为两步:计算注意力系数(attention coefficient)和加权求和(aggregate)
input
单个 graph attentional layer的输入是一个节点特征向量集合
h = { h 1 ⃗ , h 2 ⃗ , … , h N ⃗ } , h i ⃗ ∈ R F h=\lbrace \vec{h_1},\vec{h_2},\dots,\vec{h_N} \rbrace,\; \vec{h_i}\in R^F h={h1,h2,…,hN},hi∈RF
其中
- N N N表示节点的数目
- F F F表示每个节点的特征的数目
output
并生成一个新的节点特征集合
h ′ = { h 1 ′ ⃗ , h 2 ′ ⃗ , … , h N ′ ⃗ } , h i ′ ⃗ ∈ R F ′ h^{'}=\lbrace \vec{h_1^{'}},\vec{h_2^{'}},\dots,\vec{h_N^{'}} \rbrace,\; \vec{h_i^{'}}\in R^{F^{'}} h′={h1′,h2′,…,hN′},hi′∈RF′
其中 F F F和 F ′ F' F′具有不同的维度。
为了得到相应的输入与输出的转换,需要根据输入的feature至少一次线性变换得到输出的feature,所以我们需要对所有节点训练一个权值矩阵: W ∈ R F ′ × F W\in R^{F^{'}\times F} W∈RF′×F,这个权值矩阵就是输入与输出的F个feature与输出的F’个feature之间的关系:
h i ′ ⃗ = W h i ⃗ \vec{h_i^{'}}=\mathbf{W}\vec{h_i} hi′=Whi
为了获得足够的表达能力以将输入特征变换为更高级别的特征,需要至少一个可学习的线性变换。为此,作为初始步骤,一个共享的线性变换参数矩阵 W ∈ R F ′ × F \mathbf{W}\in R^{F^{'}\times F} W∈RF′×F被应用于每一个节点。
计算注意力系数(attention coefficient)
论文里说,self-attention是一种Global graph attention,会将注意力分配到图中所有的节点上,这种做法显然会丢失结构信息。通过self-attention注意力机制可以计算任意两个样本的关系,使一个样本用其他所有样本来表示,但是第一,基于空间相似假设,一个样本与一定范围内的样本关系较密切,第二,样本较多的时候,计算量非常大。为了解决这一问题,作者使用了一种 masked attention 的方法,对于一个样本来说只利用邻域内的样本计算注意力系数和新的表示,即仅将注意力分配到节点的一阶邻居节点集上。
针对每个节点执行 self-attention机制,机制 a a a为
a : R F ′ × R F ′ → R a:R^{F^{'}}\times R^{F^{'}}\to R a:RF′×RF′→R
计算注意力互相关系数attention coefficients:
e i j = a ( W h i ⃗ , W h j ⃗ ) (1) \tag{1} e_{ij}=a(\mathbf{W}\vec{h_i}, \mathbf{W}\vec{h_j}) eij=a(Whi,Whj)(1)
其中
- 注意力系数 e i j e_{ij} eij表示的节点 j j j对于节点 i i i的重要性
- 向量 h ⃗ \vec{h} h就是 feature向量
- a a a是一个 R F ′ × R F ′ → R R^{F^{'}}\times R^{F^{'}}\to R RF′×RF′→R的映射
- W ∈ R F ′ × F \mathbf{W}\in R^{F^{'}\times F} W∈RF′×F,使用 W \mathbf{W} W将每个特征转换为可用的表达性更强的特征
为了使得注意力系数更容易计算和便于比较,引入了softmax对所有的 i i i的相邻节点 j j j进行正则化:
α i j = s o f t m a x j ( e i j ) = exp ( e i j ) ∑ k ∈ N i exp ( e i k ) (2) \tag{2} \alpha_{ij} = \mathrm{softmax}_j (e_{ij}) = \frac{\exp(e_{ij})}{\sum_{k \in \mathcal{N}_i} \exp(e_{ik})} αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)(2)
其中
- N i \mathcal{N_i} Ni表示节点 i i i的邻居节点集合
- 这个系数 α \alpha α就是每次卷积时,用来进行加权求和的系数
实验中,注意力机制 a a a是一个单层的前馈神经网络,通过权值向量来确定 a ⃗ ∈ R 2 F ′ \vec{\text{a}} \in \mathbb{R}^{2F'} a∈R2F′,并且加入了 LeakyRelu的非线性激活,这里小于零斜率为0.2。(回顾下几种Relu函数,relu:小于0就是0,大于零斜率为1;LRelu:小于零斜率固定一个值,大于零斜率为1;PRelu:小于零斜率可变,大于零斜率为1;还有CRelu,Elu,SELU)。
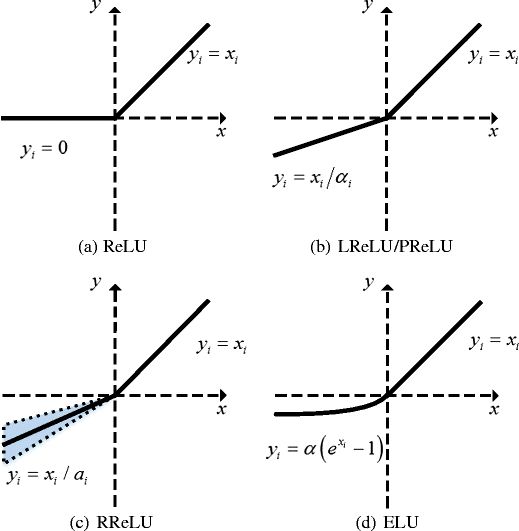
α i j = exp ( L e a k y R e L U ( a ⃗ T [ W h ⃗ i ∥ W h ⃗ j ] ) ) ∑ k ∈ N i exp ( L e a k y R e L U ( a ⃗ T [ W h ⃗ i ∥ W h ⃗ k ] ) ) (3) \tag{3} \alpha_{ij} = \frac{ \exp{ ( \mathrm{LeakyReLU} ( \vec{\text{a}}^T [\mathbf{W} \vec{h}_i \Vert \mathbf{W} \vec{h}_j ] ))}}{\sum_{k \in \mathcal{N_i}} \exp{(\mathrm{LeakyReLU}(\vec{\text{a}}^T [\mathbf{W} \vec{h}_i \Vert \mathbf{W} \vec{h}_k]))}} αij=∑k∈Niexp(LeakyReLU(aT[Whi∥Whk]))exp(LeakyReLU(aT[Whi∥Whj]))(3)
其中
- ||表示concatenation操作(串联)
下图就是表示 W h ⃗ i \mathbf{W} \vec{h}_i Whi和 W h ⃗ j \mathbf{W} \vec{h}_j Whj经过串联以后,再和权值向量 a ⃗ ∈ R 2 F ′ \vec{\text{a}} \in \mathbb{R}^{2F'} a∈R2F′相乘后,最后进行一个softmax归一化处理后的示意图。
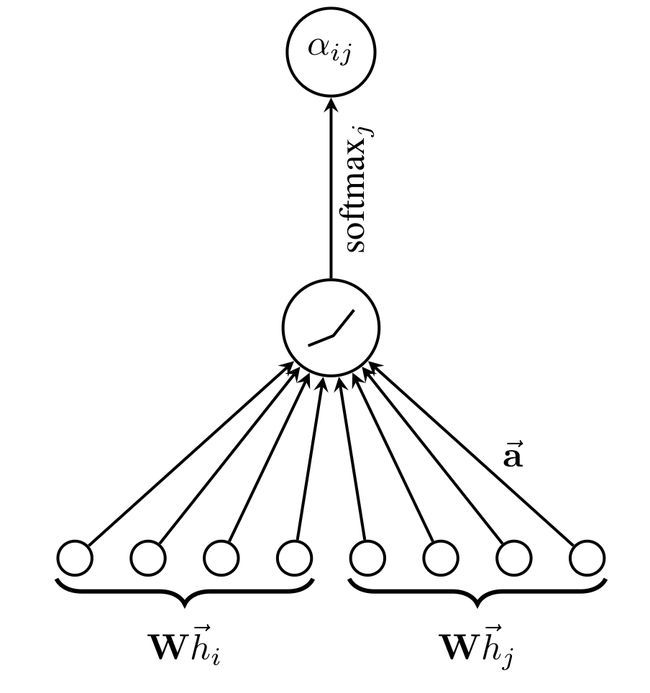
这部分代码为
def forward(self, x):
# [B_batch,N_nodes,C_channels]
B, N, C = x.size()
# h = torch.bmm(x, self.W.expand(B, self.in_features, self.out_features)) # [B,N,C]
h = torch.matmul(x, self.W) # [B,N,C]
a_input = torch.cat([h.repeat(1, 1, N).view(B, N * N, C), h.repeat(1, N, 1)], dim=2).view(B, N, N,
2 * self.out_features) # [B,N,N,2C]
# temp = self.a.expand(B, self.out_features * 2, 1)
# temp2 = torch.matmul(a_input, self.a)
attention = self.leakyrelu(torch.matmul(a_input, self.a).squeeze(3)) # [B,N,N]
attention = F.softmax(attention, dim=2) # [B,N,N]
attention = F.dropout(attention, self.dropout, training=self.training)
h_prime = torch.bmm(attention, h) # [B,N,N]*[B,N,C]-> [B,N,C]
out = F.elu(h_prime + self.beta * h)
return out
加权求和(aggregate)
得到归一化的注意力系数后,使用归一化的值计算对应特征的线性组合,作为每个顶点最后的输出特征(最后可以加一个非线性层, σ \sigma σ):
h ⃗ i ′ = σ ( ∑ j ∈ N i α i j W h ⃗ j ) (4) \tag{4} \vec{h}'_i = \sigma(\sum_{j \in \mathcal{N}_i} \alpha_{ij} \mathbf{W} \vec{h}_j) hi′=σ(j∈Ni∑αijWhj)(4)
h ⃗ i ′ \vec{h}'_i hi′就是GAT输出的节点 i i i 融合了邻域信息的新特征
multi-head attention机制
为了使self-attention 的学习过程更稳定,发现使用 multi-head attention来扩展注意力机制是很有效的。
使用K个独立的 attention 机制执行公式式4这样的变换,然后他们的特征连(concatednated)在一起,就可以得到如下的输出:
h ⃗ i ′ = ∥ k = 1 K σ ( ∑ j ∈ N i α i j k W k h ⃗ j ) (5) \tag{5} \vec{h}'_i = \Vert^{K}_{k=1} \sigma(\sum_{j \in \mathcal{N}_i} \alpha^k_{ij} \mathbf{W}^k \vec{h}_j) hi′=∥k=1Kσ(j∈Ni∑αijkWkhj)(5)
其中
- 最后的返回输出 h ′ h' h′,每个顶点都会有 K F ′ KF' KF′维的特征(不是 F ′ F' F′)
下图表示 K = 3 K=3 K=3时的multi-head attention机制示意图。例如此图,节点1在邻域中具有多端注意机制,不同的箭头样式表示独立的注意力计算,通过连接或平均每个head获取 h ⃗ 1 \vec{h}_1 h1。
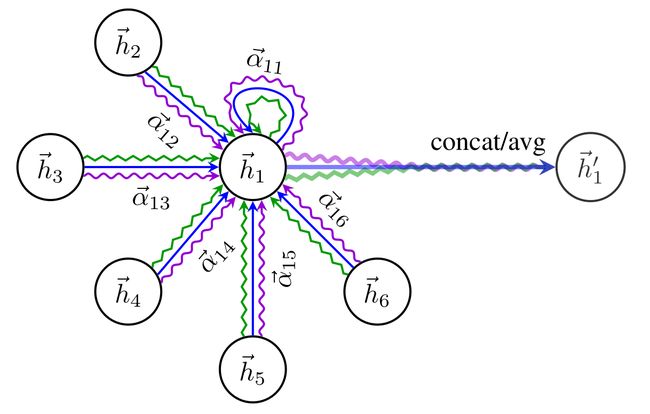
对于最后一个卷积层,如果还是使用multi-head attention机制,那么就不采取连接的方式合并不同的attention机制的结果了,而是采用求平均的方式进行处理,即
h ⃗ i ′ = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i α i j k W k h ⃗ j ) (6) \tag{6} \vec{h}'_i = \sigma(\frac{1}{K} \sum^K_{k=1} \sum_{j \in \mathcal{N}_i} \alpha^k_{ij} \mathbf{W}^k \vec{h}_j) hi′=σ(K1k=1∑Kj∈Ni∑αijkWkhj)(6)
2.2 和当前工作的对比
- 计算高效:self-attention层的操作可以在所有的边上并行,输出特征的计算可以在所有顶点上并行。没有耗时的特征值分解。单个的GAT计算 F ′ F' F′个特征的时间复杂度可以压缩至 O ( ∣ V ∣ F F ′ + ∣ E ∣ F ′ ) O(|V|FF'+|E|F') O(∣V∣FF′+∣E∣F′),F是输入的特征数,|V|和|E|是图中顶点数和边数。复杂度与Kipf & Welling, 2017的GCN差不多。
尽管 multi-head 注意力将存储和参数个数变为了K倍,但是单个head的计算完全独立且可以并行化。 - 鲁棒性更强:和GCN不同,本文的模型可以对同一个 neighborhood的node分配不同的重要性,使得模型的capacity大增。
- 注意力机制以一种共享的策略应用在图的所有的边上,因此它并不需要在之前就需要得到整个图结构或是所有的顶点的特征(很多之前的方法的缺陷)。因此GAT 也是一种局部模型。也就是说,在使用 GAT 时,无需访问整个图,而只需要访问所关注节点的邻节点即可,解决了之前提出的基于谱的方法的问题。因此这个方法有几个影响:
- 图不需要是无向的,可以处理有向图(若 j → i j\to i j→i不存在,仅需忽略 α i j \alpha_{ij} αij即可)
- 可以直接应用到 inductive learning:包括在训练过程中在完全未见过的图上评估模型的任务上。
- 2017年Hamilton提出的归纳学习方法(GraphSAGE)为每一个node都抽取一个固定尺寸的neighborhood,为了计算的时候footprint是一致的(指的应该是计算的时候处理neighborhood的模式是固定的,不好改变,因此每次都抽样出固定数量的neighbor参与计算),这样,在计算的时候就不是所有的neighbor都能参与其中。此外,Hamilton的这个模型在使用一些基于LSTM的方法的时候能得到最好的结果,这样就是假设了每个node的neighborhood的node一直存在着一个顺序,使得这些node成为一个序列。但是本文提出的方法就没有这个问题,每次都可以将neighborhood所有的node都考虑进来,而且不需要事先假定一个neighborhood的顺序
解析:GraphSAGE:Inductive Representation Learning on Large Graphs - 和MoNet(Monti et al., 2016)相比,GAT模型使用顶点特征计算相似性,而不是顶点的结构特征
3 实验和评价
实验分成两部分,transductive learning(半监督学习)和inductive learning(归纳学习)。
数据集
图结构的数据集,以及数据集之中的信息如下:
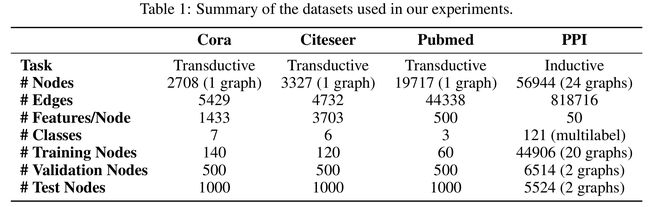
半监督学习transductive learning
- 两层 GAT
- 在Cora 数据集上优化网络结构的超参数,应用到Citeseer数据集
- 第一层 8 head, F’=8 , ELU 作为非线性函数
- 第二层为分类层,一个 attention head 特征数C,后跟 softmax 函数,为了应对小训练集,正则化(L2)
- 两层都采用 0.6 的dropout,相当于计算每个node位置的卷积时都是随机的选取了一部分近邻节点参与卷积
- 用Glorot初始化初始的,并且是用Adam SGD来最小化交叉熵进行优化
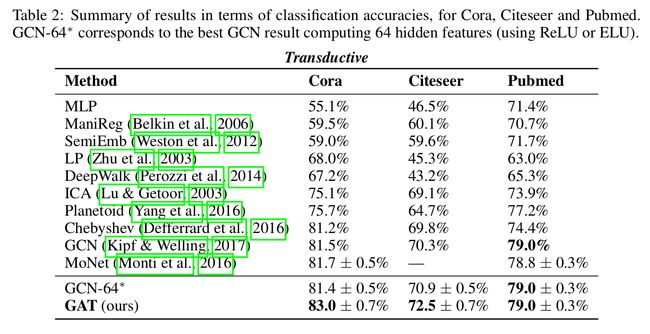
归纳学习inductive learning
- 三层GAT 模型
- 前两层 K=4, F’=256 ,ELU作为非线性函数
- 最后一层用来分类 K=6, F`=121 , 激活函数为sigmoid
- 该任务中,训练集足够大不需要使用 正则化 和 dropout
- 用Glorot初始化初始的,并且是用Adam SGD来最小化交叉熵进行优化
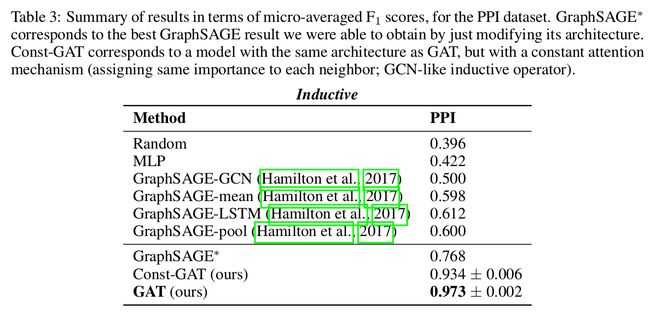
最后,使用t-SNE(Maaten & Hinton, 2008)在Cora数据集上进行一层GAT模型的输出变换图如下所示

4 总结
GAT模型的特点
- 计算高效:self-attention层的操作可以在所有的边上并行,输出特征的计算可以在所有顶点上并行。没有耗时的特征值分解。单个的GAT计算 F ′ F' F′个特征的时间复杂度可以压缩至 O ( ∣ V ∣ F F ′ + ∣ E ∣ F ′ ) O(|V|FF'+|E|F') O(∣V∣FF′+∣E∣F′),F是输入的特征数,|V|和|E|是图中顶点数和边数。复杂度与Kipf & Welling, 2017的GCN差不多。
尽管 multi-head 注意力将存储和参数个数变为了K倍,但是单个head的计算完全独立且可以并行化。 - 鲁棒性更强:和GCN不同,本文的模型可以对同一个 neighborhood的node分配不同的重要性,使得模型的capacity大增。
- 注意力机制以一种共享的策略应用在图的所有的边上,因此它并不需要在之前就需要得到整个图结构或是所有的顶点的特征(很多之前的方法的缺陷)。因此GAT 也是一种局部模型。也就是说,在使用 GAT 时,无需访问整个图,而只需要访问所关注节点的邻节点即可,解决了之前提出的基于谱的方法的问题。因此这个方法有几个影响:
- 图不需要是无向的,可以处理有向图(若 j → i j\to i j→i不存在,仅需忽略 α i j \alpha_{ij} αij即可)
- 可以直接应用到 inductive learning:包括在训练过程中在完全未见过的图上评估模型的任务上。
GAT模型的局限及未来的研究方向
- 使用稀疏矩阵操作的GAT层,可以将空间复杂度降低到顶点和边数的线性级别,使得GAT模型可以在更大的图数据集上运行。然而,文中使用的tensor操作框架只支持二阶tensor的稀疏矩阵乘法,限制了当前实现的版本的模型能力(尤其在有多个图的数据集上)。解决这个问题是未来的一个重要研究方向。在这些使用稀疏矩阵的场景下,在某些图结构下GPU的运算并不能比CPU快多少。
- 另一个需要注意的地方是GAT模型的感受野的大小的上界取决于网络的深度(与GCN和其他模型相似)。像skip connections(He et al., 2016)这样的技术可以来近似的扩展模型的深度。
- 在所有边上的并行计算,尤其是分布式的计算可以设计很多冗余的计算,因为图中的邻居往往高度重叠。
- 扩展GAT模型从顶点分类到图分类也是一个更具应用性的方向
- 扩展GAT模型到整合边的信息(可能表示节点之间的关系)可以处理更多的问题
GAT核心公式
图注意力模型GAT用注意力机制替代了图卷积中固定的标准化操作。下图和公式定义了如何对第 l l l层节点特征做更新得到第 l + 1 l+1 l+1层节点特征:

z i ( l ) = W ( l ) h i ( l ) (1) \tag{1} z_{i}^{(l)}=\mathbf{W}^{(l)} h_{i}^{(l)} zi(l)=W(l)hi(l)(1)
e i j ( l ) = LeakyReLU( a ⃗ ( l ) T ( z i ( l ) ∥ z j ( l ) ) ) (2) \tag{2} \left.e_{i j}^{(l)}=\text { LeakyReLU( } \vec{a}^{(l)^{T}}\left(z_{i}^{(l)} \| z_{j}^{(l)}\right)\right) eij(l)= LeakyReLU( a(l)T(zi(l)∥zj(l)))(2)
α i j ( l ) = exp ( e i j ( l ) ) ∑ k ∈ N ( i ) exp ( e i k ( l ) ) (3) \tag{3} \alpha_{i j}^{(l)}=\frac{\exp \left(e_{i j}^{(l)}\right)}{\sum_{k \in \mathcal{N}(i)} \exp \left(e_{i k}^{(l)}\right)} αij(l)=∑k∈N(i)exp(eik(l))exp(eij(l))(3)
h i ( l + 1 ) = σ ( ∑ j ∈ N ( i ) α i j ( l ) z j ( l ) ) (4) \tag{4} h_{i}^{(l+1)}=\sigma\left(\sum_{j \in \mathcal{N}(i)} \alpha_{i j}^{(l)} z_{j}^{(l)}\right) hi(l+1)=σ⎝⎛j∈N(i)∑αij(l)zj(l)⎠⎞(4)
multi-head attention机制
神似卷积神经网络里的多通道,GAT 引入了多头注意力来丰富模型的能力和稳定训练的过程。每一个注意力的头都有它自己的参数。如何整合多个注意力机制的输出结果一般有两种方式:
- 拼接
h i ( l + 1 ) = ∥ k = 1 , . . . , K σ ( ∑ j ∈ N ( i ) α i j k W k h j ( l ) ) (5) \tag{5} h_{i}^{(l+1)}=\|_{k=1, ..., K} \sigma\left(\sum_{j \in N(i)} \alpha_{i j}^{k} W^{k} h_{j}^{(l)}\right) hi(l+1)=∥k=1,...,Kσ⎝⎛j∈N(i)∑αijkWkhj(l)⎠⎞(5) - 平均
h i ( l + 1 ) = σ ( 1 k ∑ k = 1 K ∑ j ∈ N ( i ) α i j k W k h j ( l ) ) (6) \tag{6} h_{i}^{(l+1)}=\sigma\left(\frac{1}{k} \sum_{k=1}^{K} \sum_{j \in N(i)} \alpha_{i j}^{k} W^{k} h_{j}^{(l)}\right) hi(l+1)=σ⎝⎛k1k=1∑Kj∈N(i)∑αijkWkhj(l)⎠⎞(6)
对于上述公式的一些解释:
- 公式(1)对 l l l层节点的embedding h i ( l ) h_{i}^{(l)} hi(l)做了一个线性变换, W ( l ) \mathbf{W}^{(l)} W(l)是一个该变换的一个可训练的参数
- 公式(2)计算了成对节点间的原始注意力分数。它首先拼接了两个节点的embedding z z z,注意 ∥ \| ∥在这里表示拼接;随后对拼接好的embedding以及一个可学习的权重向量 a ⃗ ( l ) \vec{a}^{(l)} a(l)做点积;最后应用了一个LeakyReLU激活函数。这一形式的注意力机制通常被称为加性注意力,区别于Transformer(Attention Is All You Need)里的点积注意力
- 公式(3)对于一个节点所有入边得到的原始注意力分数应用了一个softmax操作,得到了注意力权重
- 公式(4),形似GCN的节点特征更新规则,对所有邻节点的特征做了基于注意力的加权求和
- 公式(5)、(6)作者建议对中间层使用拼接对最后一层使用求平均
GAT的DGL实现
参考:https://github.com/dmlc/dgl/tree/master/examples/pytorch/gat
有错误的地方还望不吝指出,欢迎进群交流GNNs&GCNs(入群备注信息!!!,格式:姓名 -(学校或其他机构信息)- 研究方向)。
参考
Graph Attention Network (GAT)
DGL博客 | 深入理解图注意力机制