数据结构与算法(Python)-一般概念和算法效率分析

写在前面

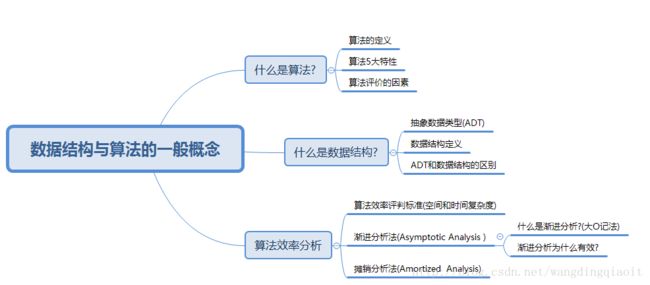
前面学习完了Python基础内容后，从本节开始正式学习数据结构与算法相关内容。这是一个比较复杂的主题，一般分为初级、高级、以及专门的算法分析三个阶段来学习，因此我们也需要循序渐进。本节主要熟悉数据结构与算法中一般概念，然后熟悉算法效率分析的大O记法，知识结构如下图所示：

什么是算法？

1)算法的定义

算法(Algorithm)，指的是对特定问题求解步骤的一种描述。
在数学上，它是运算步骤的有限序列，每一步代表执行某种运算。例如，手动计算两个整数和的算法描述为: 将两个数字对齐写在纸上，然后从个位开始，逐位求和，遇到和大于10则向高位进位，最终计算出两个数字之和。

在计算机中，算法是指令的有限序列，每条指定代表一个或者多个操作。例如，在12306网站完成车票查询、车票订购等任务，在计算机上都是由一系列算法实现。

在利用计算机求解问题的过程中，我们首先对问题进行建模，构造合适的算法，然后编写相关程序，流程如下(来自Introduction to Algorithm)：

2)算法的5大特性

对于一个算法，有5大特性，列出如下：

• 输入 一个算法有零个或者多个外部输入,注意可以没有输入。

• 输出 一个算法有一个或者多个输出，注意算法必定有某种形式的输出。

• 有穷性(Finiteness) 算法必须在有限步骤内完成。

• 确定性(Definiteness ) 算法中每条指定必须没有二义性（只有一种解释），在任何条件下，算法只有唯一的一条执行路径，对于相同的输入只能得到相同的输出。

• 可行性（Effectiveness ） 算法中描述的操作都可以通过已经实现的基本操作执行有效次实现，具有可行性。

3) 算法评价的因素

解决同一个问题有不同的方法，这些方法之间如何比较和选择成为一个关键。

例如去不同城市，可以选择的交通方式有火车、轮船、飞机、自驾、客运大巴、拼车等多种，这些不同的旅行方式，在舒适度、价钱、时间、安全等方面各有不同，需要从多个角度比较和选择。

评价算法好坏也有各种因素，主要包括下面几个因素：

• 正确性 是否正确地解决了问题？

• 可读性 算法主要是人来编写，其次才是机器执行。是否容易理解成为实现和维护的关键。

• 实现难度 算法是否容易实现？

• 存储开销 算法消耗的内存、外存储空间合理吗？

• 执行时间 算法执行时耗时能接受吗？

• 健壮性 程序遇到非预期输入能否做出合理反应? 例如简单的计算程序，遇到除0操作时，应该提醒用户错误，而不是程序崩溃掉。

什么是数据结构？

1）抽象数据类型

利用计算机求解问题的首要步骤是对问题进行建模，在建模的过程中，我们需要考虑到数据的输入、处理、输入等内容，算法描述了操作这些数据的具体流程，但是如何表示和存储问题模型中的数据则需要选择或者重新设计一种有利的结构。
抽象数据类型（Abstract Data Types，ADT），是一种理论上的概念，它从逻辑层面，描述了可能值范围、允许的操作以及操作的行为表现。ADT与具体的实现细节无关（implementation-independent ）。例如整数，是一种ADT，它可能的值包括-1,0,1…，允许的操作包括加减乘除，以及大于、小于比较等。这些是数学上的模型，与在计算中具体如何表示无关。

2）数据结构

ADT是一种理论上的数学模型，而数据结构则是计算机上对这个抽象数据类型的实现，是实现层面的概念，由具体计算机语言以及这个语言的基础类型来实现。

3）ADT与数据结构的区别

从上面的定义可以看出了它们之间的差别。例如栈(Stack)是一种ADT，定义了它是先进后出的结构，支持的操作包括：入栈(push)、出栈(pop)、查看栈顶元素(top)、判断栈是否为空(empty)等4种操作。在计算上可以通过数组实现，称为ArrayStack，或者通过链表实现，称为LinkListStack。这两种具体实现称之为栈的数据结构。

算法效率评判标准

上面提到了，如果我们评价交通工具，我们可能会选择舒适度、时间、安全、价格等标准进行评判，与此类似，评判一个算法好坏也需要一些标准。

对一个算法进行空间和时间复杂度分析时，可以通过执行完程序后进行统计分析(事后统计方法)，也可以在未执行程序时就进行理论分析(事前估算分析估计方法)。对于同一个算法，在不同的机器上执行，受到处理器、机器字长、存储空间、指令集等的影响，运行时间存在差异，例如运行在“天河一号”超级计算机和普通PC上的程序，运行时间就可能大不相同；同一个算法，即使利用同一台机器来运行程序，但采用C或者Ada编写的程序就比用Basic或者Lisp编写的快约20倍。因此，事后统计分析的方法很多时候并不可靠(为特定设备编写的程序进行性能比较除外)，因此人们常常采用事先分析估算的方法。

既然事先估算方法，并没有实际执行程序，使用绝对单位的字节大小或者时间长度，显然是不可能的了，应该使用某种理论上的抽象标准。在上面我们提到了诸如可读性、正确性等因素，这些因素是每个好的算法都必须具备的，这些因素没有区分度，真正具有区分度的因素是空间复杂度(Space Complexity)和时间复杂度（Time Complexity）两个标准。这两个复杂度，一般随着问题输入的数据量，即与问题规模n，成某种函数关系，例如时间复杂度可以表示为:
T(n)=f(n) 。

在寻求这个函数关系时，我们首先找出一种被作为基本操作(Elementary operation)的运算，估算它的执行次数与n的关系。所谓基本操作指的是算法中对时间有着关键影响，与问题规模成正比的操作。例如检查一个元素x是否在一组数字a中，比较x与a中某个元素值是否相等的操作，就可以视为基本操作。

def find_in_array(array,val):
    """
    naive search algorithm
    :param array: input elements array
    :param val:  the value to search
    :return: index if found or -1
    """
    for i, x in enumerate(array):
        if x == val:   # 基本操作
           return i
    return -1

在上面的查找过程中，我们会遇到3种情形:

• 最坏情况下(worst-case) 要查找的元素在数组最后一个位置 T(n)=n
• 平均情况下(average case) 假定每个元素被查找的概率相同，则平均查找时需要的比较次数为: T(n)=∑ni=11n∗i=1+n2
• 最好情况下(best-case) 要查找的元素在数组第一个位置 T(n)=1

下面我们来重点熟悉时间复杂度的大O记法。

渐进分析法

1)什么是渐进分析法?

渐进分析法（Asymptotic Analysis）的目标是寻找到问题处理的时间与问题规模之间，随着问题规模变大时的一种上限和下限关系，通过上限我们了解到算法最坏情况，通过下限了解到算法最好的情况。

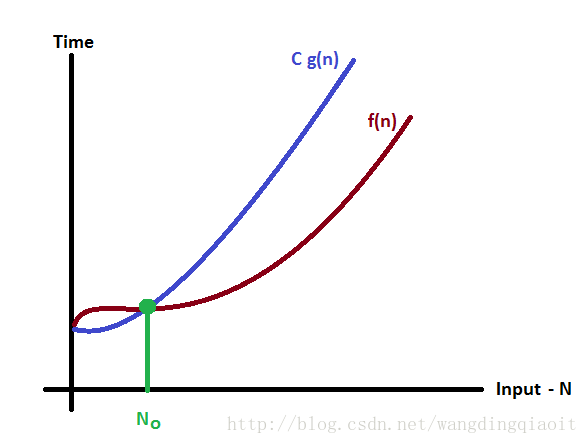
大O定义: 假设 f(n) 是算法时间复杂度的表示，而 g(n) 是其中最具影响的因子，如果: f(n)<=Cg(n) ，对于所有的 n>=n0,C>0,n0>=1 都成立，则我们可以将 f(n) 记为: f(n)=O(g(n))

上面定义中，最具影响的因子，是复杂度表达式中，对结果影响最大的部分，例如: f(n)=5n2+2n+1 ，那么当n增大时，显然 n2 决定了 f(n) 的大小，这个因子就是上面定义中的 g(n) 。

f(n) 与 g(n) 关系如下图所示:

例如, f(n)=3n+2 , g(n)=n ，令: f(n)<=Cg(n)⇒3n+2<=Cn ，求解这个不定方程，可以得到: C=4,n>=2 时: f(n)<=Cg(n) 成立，因此有: f(n)=O(n) 。

除了大O记法，还有一个表达复杂度下界的 f(n)=Ω(g(n)) 记法，和表达复杂度平均界限的 f(n)=Θ(g(n)) 记法，在算法分析中，我们通常考虑的是算法的上界，即最坏情况下的表现，对于另外两种记法，感兴趣地可以参考Asymptotic Notation，这里不再详细展开。

2)渐进分析法为什么有效？

引用一个来自[1]的例子，假设时间复杂度表示为:
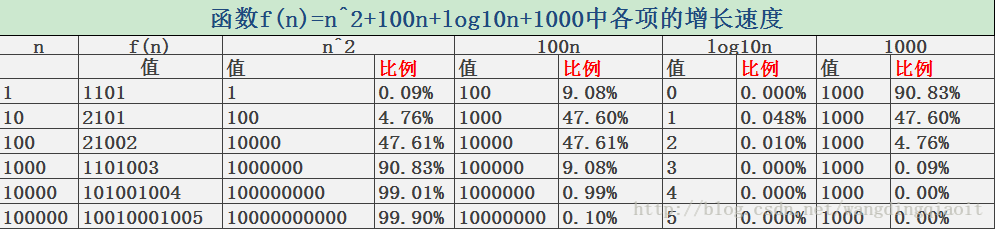
f(n)=n2+100n+logn10+1000 ，当n逐渐增大时，我们统计如下表所示:

从这个表可以看出，当n=1,10时，100n和1000所占比重较大；当n=100时，n平方和100n所占比重相同；当n>100后，n平方所占比重越来越大，到最后n=100000时，n平方接近100%。这就说明，使用n平方来近似表达f(n)的计算复杂度是完全可行的，也就是 f(n)=O(n2) 。

摊销分析法

摊销分析法(Amortized analysis)是从操作序列的角度分析算法的一种方法，考虑的是当执行某个操作n次时，运行时间和资源消耗的平均情况。

例如有一个动态分配的数组，当空间足够时，在尾部添加(push, 不是insert)一个新元素需要的 T(n)=1 ；但是当空间不够时，需要重新分配连续空间，并把之前的元素复制到这块连续空间，这个时候添加元素的时间复杂度变成了 T(n)=n 。那么是不是添加n个元素时，最坏情况就变成了 T(n)=n∗n=n2 了？

答案是否定的，上面的分析过于悲观，因此需要利用摊销分析法，对插入n个元素的复杂度进行分析。在上面插入过程中，一个重要的事实是: 并不是每次插入，都要复制元素，仅当空间不足时才会进行复制操作，而这个复制操作引起的开销在这n次操作中平摊下来就变小了。

假设我们数组初始大小为1，自增因子为2，那么这个变化过程如下表格所示(例子整理自Algorithmic Complexity):

添加序号	复制次数	一共消耗	数组旧的大小	数组新的大小
1	0	1	1	-
2	1	2	1	2
3	2	3	2	4
4	0	1	4	-
5	4	5	4	8
6	0	1	8	-
7	0	1	8	-
8	0	1	8	-
9	8	9	8	16

假设 T(i)=1+Ci ,其中 Ci 为复制元素的开销:

Ci={2m,i=2m+1(m=0,1,2...)0,其他情况

假设添加n个元素时数组最多需要扩容m次，则有: 2m≥n ,m取整数，则有: m≤logn2+1

则n次添加的代价之和为:
T(n)=∑ni=1T(i)≤n+∑mj=12j−1=n+2n−1=3n−1
对n次添加进行平摊后，添加一个元素的时间复杂度为: T(n)/n=O(1)

这个分析表明，虽然向动态数组添加元素存在O(n)的情况，但是平摊下来每个添加操作的时间复杂度仍然为O(1)，因此不用过于悲观。上面的这种分析方法称之为总和法(Aggregate Method)。

注意： 这里平摊后的时间复杂度，和上面渐进分析得出的平均情况复杂度，并不是同一个概念。渐进分析的平均情况，使用了概率假设，例如假设数组中每个元素被查找的概率相同这种假定，但是摊销分析并没有对输入进行任何假设。摊销分析强调的是对一个操作执行多次时的序列进行分析，将这种总的时间复杂度平摊到每一个操作之上从而得出最终的复杂度。

摊销分析方法，除了上面介绍的这种总和法，还有其他方法，感兴趣地可以自行参考Amortized Analysis。

本节介绍了数据结构与算法中的一般概念，以及算法分析中常用的大O记法和摊销分析方法，这只是一个入门，算法分析一般作为专门课程是一个需要深入学习的主题，已经超过了本节范畴，后面会循序渐进地进行相关学习。

参考资料

• [1] 数据结构与算法 c++版 第三版 Adam Drozdek编著 清华大学出版社
• [2] 数据结构 严蔚敏 吴伟明 清华大学出版社
• Amortized analysis
• Amortized Analysis
• Introduction to Algorithm
• Abstract data type vs Data Type vs Data Structure, with respect to object-oriented programming
• Abstract data type
• Algorithmic Complexity