龙书学习 第三章练习题
3.1.1
float limitedSquare(x){float x;
/* returns x-squared, but never more than 100 */
return (x<=-10.0||x>=10.0)?100:x*x;
}3.1.2
Here is a photo of my house;

See More Picture if you
liked that one.
3.3.1 略
3.3.2
1) 首尾为a,中间段是零或多个a或b组成的串
2) 由零或多个或为a,或为空,或为a及零或多个b,或为多个b组成的串
3) 由零或多个a或b,且末尾为aab或aba或aaa或abb组成的串
4) 在三个b产生的四个间隙中插入零或多个a组成的串
5) 或空,或为aa或bb组成的串,或在偶数个ab或者ba产生的间隙中插入零或多个aa或bb组成的串
3.3.3
1) n+1
2) n+1
3) n-1
4) 近似于于求解0<=x+y<=n的非负整数解的个数
但需要注意,唯一的特例是x+y=n的解都是等价的
所以t=n(n+1)/2+1
5) 每个字符有两种状态,出现或不出现在子序列中
因此2^n
3.3.4 insensitive -> character | capital
character -> [a-z]
captital -> [A-Z]
select->s|S e|E l|L e|E c|C t|T
3.3.5
1) a*e*i*o*u*
2) a*b*c*d*e*f*g*h*i*j*k*l*m*n*o*p*q*r*s*t*u*v*w*x*y*z*
3) / \* (.*\"/\*.*/\*.*)* \*/
4) 查了一下 (?!.*?(\d).*?\1.*?$)\d+ 喵喵喵?先放着
5) 跟4)有一定联系,先放着
6) even_a_even_b -> (aa|bb)*((ab|ba)(aa|bb)*(ab|ba)(aa|bb)*)*
even_a_odd_b-> even_a_even_b a(aa|bb)*(ab|ba) even_a_even_b (写法应该较多,都是一个意思)
7) 不懂国际象棋,跳过
8) b*(ab?)*
9) b*a+b?a*
3.3.6
1) [a-jA-J]
2) [^(aeiou)]
3) [0-9a-f]
4) [!\.\?]
3.3.7 \"\\
3.3.8 全集是有限的,那么补集一定是存在且有限的。
3.3.9 r{m,n} <=> r.....(m个r)......rr?....(n-m个r?)....r?
3.3.10
1) 在一个[]中首位的^表示补集字符,在整个串首位表示最左端
2) 可以的,同时存在的^和$和省略了没区别;^a可以等价写成a.*;同理a$
3.3.11 *.*
3.3.12 _ ->.
% ->.*
3.4.3
1)
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| f(s) | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 0 | 2 |
2)
| s | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| f(s) | 0 | 1 | 2 | 3 | 4 | 5 |
3)
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| f(s) | 0 | 0 | 0 | 1 | 1 | 2 | 3 |
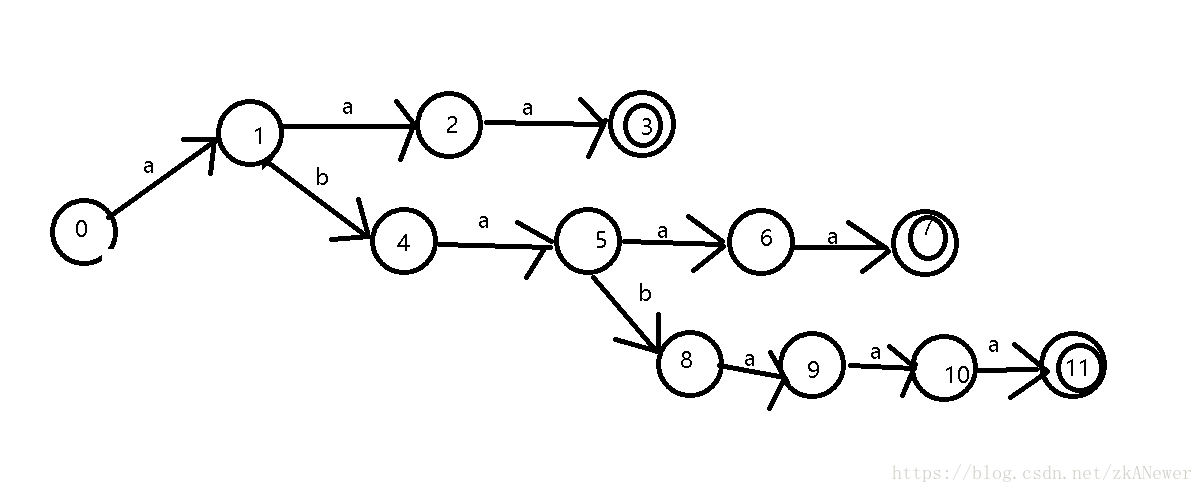
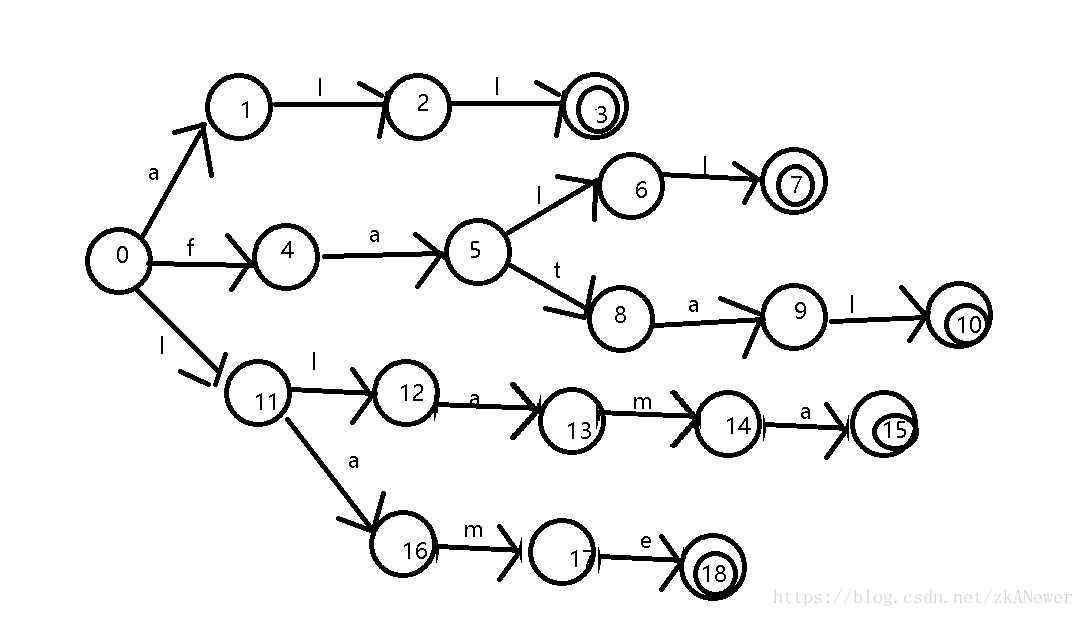
3.4.4 考虑当s 当s=k时如果bk=b(f(k-1)+1),那么最大真前缀长度+1 即对应t=t+1,f(s+1)=t 反之,则将bk对上述逻辑应用在k-1时的真前缀f(k-1)上(真前缀递归a是b的kmp串,b是c的kmp串,则a一定是c的后缀。),重复上述逻辑 3.4.5 首先分析,在整个循环中,s的值从1到n-1,t的值从0到最多n-1。我们来考虑这个最大真前缀也是最大真后缀的最长串的长度,即t的值,在每次循环至多增加1,或者进入4)向前迭代,向前迭代值必然减少。假设t=f(t)被执行了超过n次,那么t值必然减少了超过n,但t再循环中至多增加n,由此得到t值在循环结束为负,矛盾。 3.4.6 √ × 3.4.7 若i=k时,s的值是既是a1a2...ai的后缀又是b1...bn前缀的字符串的最长字符串的长度,即b1...bs。 当i=k+1时, 如果ai=bs+1,那么b1...bs+1既是a1a2...ai+1后缀又是b1...bn的前缀,并且也是最长的字符串,s自然符合要求 否则,通过失效函数,我们获得新的b1....bf(f(s))是a1...ai+1的后缀也是b1...bn的前缀,假设这个串不是最长的,那么就和失效函数的定义矛盾了。 3.4.8 同3.4.5的分析方式,循环至多进行m次,对应了扫描字符串当前扫描位置的指针移动,同样的s对应了匹配字符串当前扫描位置的指针移动,我们知道,s最多增加m次,因此3)的执行最多m次,即O(m)的时间复杂度,合并3.4.5结果即KMP算法时间复杂度O(m+n) 3.4.9 1) |Sn|=|Sn-1|+|Sn-2| <=> an=an-1+an-2 (n>2) a1=a2=1 利用特征方程解决 an=(1+δ)^n/sqrt(5)-(δ)^n/sqrt(5) 2) S6=abaababa 3) S7=abaababaabaab 4) 重点在于Sn的分解式:Sn=(Sn-2Sn-3)Sn-2=ΣSk(2<=k<=n-2)S3(奇)=ΣSk(1<=k<=n-2)S2(偶) 因此偶数式Sn=ΣSk(2<=k<=n-2)ba奇数时Sn=ΣSk(2<=k<=n-2)ab 结尾的不同是命题中j+1的由来 假设这个命题在n=t的时候成立,n=t+1的时候 St+1=StSt-1,对于j<=|St|,由假设,成立 注意到StSt-1=St-1St-2St-1 对j>|St|分析,以分隔符/表示j=|St| St-1St-2/St-1=St-2St-3St-2/St-2St-3 St-2=ΣSk(2<=k<=t-4)ba奇数时Sn=ΣSk(2<=k<=t-4)ab St-3=ΣSk(2<=k<=t-5)ba奇数时Sn=ΣSk(2<=k<=t-5)ab 注意到t-2 t-3奇偶不同,在j=|St+1|-1的时候会产生失配,因为a不匹配b 先考虑j=|St+1|,此时一定是St-1成为最大真前后缀,否则将会得到整个字符串全是a或b |St+1|-|St|=|St-1|成立 在考虑最后一个点j=|St+1|-1,他一定不与j=|St+1|的值相同,因为不是ab就是ba 所以如果其最大真前后缀长度超过 |St+1|-|St|-1,将会得到St-1最后两个字符相同的悖论! 得证 5) Sk+1=SkSk-1,一次都不会 4) 重点在于Sn的分解式:Sn=(Sn-2Sn-3)Sn-2=ΣSk(2<=k<=n-2)S3(奇)=ΣSk(1<=k<=n-2)S2(偶) 因此偶数式Sn=ΣSk(2<=k<=n-2)ba奇数时Sn=ΣSk(2<=k<=n-2)ab 结尾的不同是命题中j+1的由来 假设这个命题在n=t的时候成立,n=t+1的时候 St+1=StSt-1,对于j<=|St|,由假设,成立 注意到StSt-1=St-1St-2St-1 对j>|St|分析,以分隔符/表示j=|St| St-1St-2/St-1=St-2St-3St-2/St-2St-3 St-2=ΣSk(2<=k<=t-4)ba奇数时Sn=ΣSk(2<=k<=t-4)ab St-3=ΣSk(2<=k<=t-5)ba奇数时Sn=ΣSk(2<=k<=t-5)ab 注意到t-2 t-3奇偶不同,在j=|St+1|-1的时候会产生失配,因为a不匹配b 先考虑j=|St+1|,此时一定是St-1成为最大真前后缀,否则将会得到整个字符串全是a或b |St+1|-|St|=|St-1|成立 在考虑最后一个点j=|St+1|-1,他一定不与j=|St+1|的值相同,因为不是ab就是ba 所以如果其最大真前后缀长度超过 |St+1|-|St|-1,将会得到St-1最后两个字符相同的悖论! 得证 5) Sk+1=SkSk-1,一次都不会 3.4.10 首先这里的失效函数可能有些含糊。假设s是对应于b1b2...bn的状态,那么状态f(s)对应于最长的,既是b1...bn的后缀又是某个关键字的前缀的字符串。注意,这里f(s)是一个状态,对应图中的状态节点。 假设b1b2...bn是tire树对应的串,每一个节点都保存了子节点信息son和本身的状态值node 3.4.11 1) 2) 3) 3.4.12 主要分析f(s+1)=t这句话,在整个循环中,最多被执行了多少次,我们考虑寻找最大串的过程,但凡失配,就不会执行这里的语句,假设一直匹配成功,那么最多执行n次,n不超过关键字长度的总和。因此算法的运行时间和关键字总和有线性关系。 3.5.1 3.5.2
s
1
2
3
4
5
6
7
8
f(s)
0
0
1
1
2
3
2
3
s
1
2
3
4
5
6
7
8
9
10
11
12
13
f(s)
0
0
1
1
2
3
2
3
4
5
6
4
5
t=0;
f(1)=0;
for(s=1;s
s
1
2
3
4
5
6
7
8
9
10
11
f(s)
0
1
2
0
1
2
3
0
1
2
3
s
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
f(s)
0
11
12
0
1
2
3
0
1
2
3
11
16
17
1
1
0
0
s
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
f(s)
0
14
1
5
0
0
1
5
13
0
0
0
18
0
18
19
20
0
0
0
1
0
0
%{
/* definitions of manifest constants
LT, LE, EQ, NE, GT, GE,
WHILE, IF, THEN, ELSE, ID, NUMBER, RELOP* /
}%
/* regular definitions */
delim [ \t\n]
ws {delim}+
letter [A-Za-z_]
digit [0-9]
escape \\[\"\\]
id {letter}({letter}|{digit})*
number {digit}+(\.{digit}+)?(E[+-]?{digit}+)?
string \"({digit}|{letter}|{escape})*\"
%%
ws {/* do nothing */}
while {return(WHILE);}
if {return(IF);}
then {return(THEN);}
else {return(ELSE);}
{id} {yylval = (int) installID(); return(ID);}
{number} {yylval = (int) installNum(); return(NUMBER);}
{string} {yylval = (int) installString(); return(STRING);}
"<" {yylval = LT; return(RELOP);}
"<=" {yylval = LE; return(RELOP);}
"==" {yylval = EQ; return(RELOP);}
"!=" {yylval = NE; return(RELOP);}
">" {yylval = GT; return(RELOP);}
">=" {yylval = GE; return(RELOP);}
%%
int installID() {/* function to install the lexeme, whose first character is pointed to
by yytext, and whose length is yyleng, into the symbol table and
return a pointer thereto. */
}
int installNum() {/* similar to installID, but puts numerical constants into a separate
table. */
}
int installString() {/* similar to installID, but deletes the first '\' in escape
pattern. */
}