数据分析：留存率曲线拟合

留存率，在数据分析中，我认为是一个比较好用的指标，因为比较稳定，不会很容易受外界因素的干扰，大幅波动。例如活动，推广等。可以用来做用户的分类，做用户规模预测。

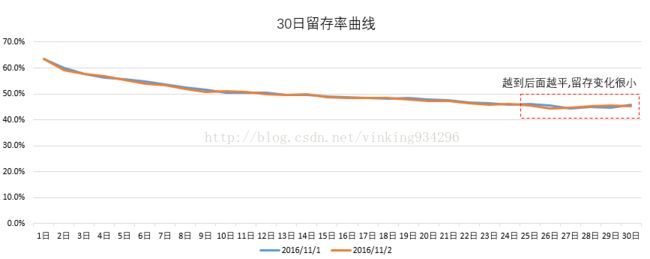
我们看到的留存曲线通常是这样的：

这里介绍几种留存率曲线拟合的方法：

1.用excel 拟合：

拟合样本，1日~12日留存率，画好曲线图后，为曲线图添加趋势线，选择对数或者幂函数(通常对数比较多)，显示公式和R平方值，R平方值越接近1，说明拟合效果越好。

如下图，蓝色曲线为真实值，拟合的橙色点线和真实值还是有差异，但效果还是不错的。

y=-0.055ln(x)+0.6382, R平方=0.9894

2.SPSS拟合

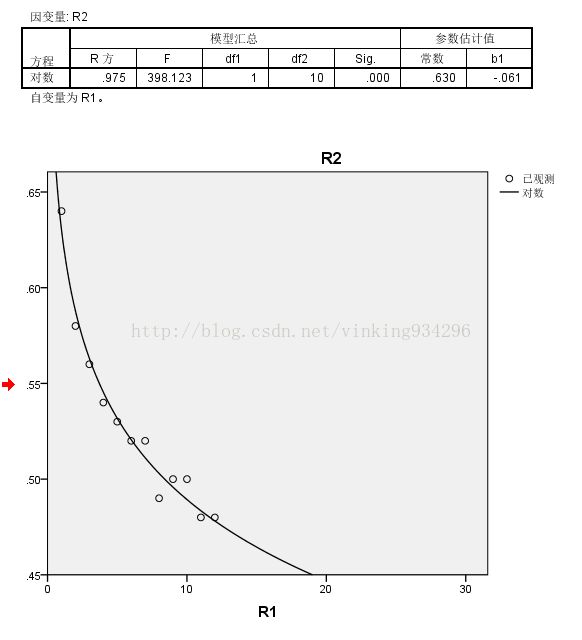
操作：R1: [1,2,3,...,12], R2 为对应的12个留存率，选择： 分析-回归-曲线估计，因变量=R2，自变量-变量=R1, 模型=对数， 保存：选预测值，残差，预测区间 - 确定 即可。

y=-0.61ln(x)+0.630 ， R平方=0.975

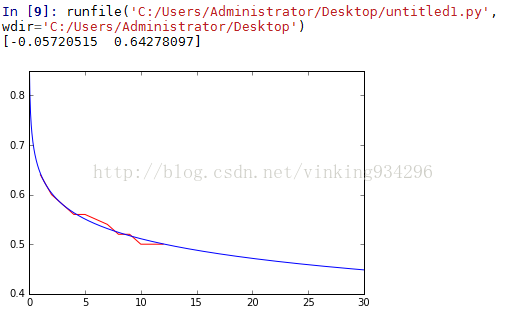
3.python拟合：

#coding:utf-8

import numpy as np
from scipy.optimize import leastsq
import pylab as pl
import math

#定义函数
#y= a*ln(x)+b

def func(x,p):
   A,B=p
   return A*np.log(x)+B


#定义残差函数
def residuals(p,y,x):
   ret=y-func(x,p)
   return ret


x3=np.linspace(0,30,1000) #用于画图精度的调节
x0=[1,2,3,4,5,6,7,8,9,10,11,12] #x变量, 在这里2,3,7全部减1
x2=np.array(x0) #向量化x变量
y0=[0.64,0.60,0.58,0.56,0.56,0.55,0.54,0.52,0.52,0.50,0.50,0.50] #y
y2=np.array(y0)#向量化
p0=[0.5,0.5]#取值起始点


qs=leastsq(residuals,p0,args=(y2,x2)) #最小二乘法
print qs[0] #为最佳的拟合函数参数
pl.plot(x0,y0,label='Real',color='red') #画出实际图像
pl.plot(x3,func(x3,qs[0]),label='sim',color='blue') #预测图像

如下图：

y=-0.0572ln(x)+0.6428

4.以上几种方式 得出的结果略有差异，不过都是可以接受的。