《算法导论》学习之旅-第十一章-散列表
文章目录
- 序言
- 直接寻址表
- 散列表
- 通过链接法解决冲突
- 散列函数
- 除法散列法
- 乘法散列法
- 全域散列表
- 开放寻址法
- 线性探测法
- 平方探测法
- 双重散列法
序言
许多应用需要一种动态集合结构,他至少支持插入,查找,删除等字典操作。而散列表就是一种实现字典操作的有效数据结构。
直接寻址表
当关键字的全域U比较小时,直接寻址是一种简单而有效的技术。为表示动态集合,我们使用了一个数组(也称为直接寻址表),记为T[0…m-1],其中每一个位置,称为槽。
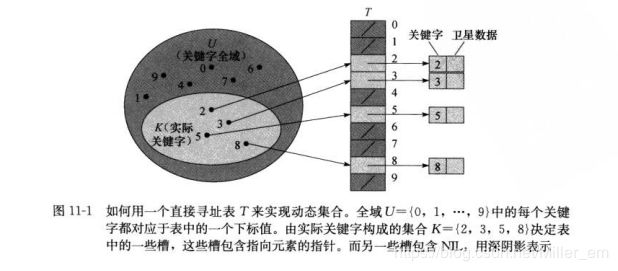
运用了直接寻址表,几个字典操作就变得相对简单:
DIRECT-ADDRESS-SEARCH(T, k)
return T[K]
DIRECT-ADDRESS-INSERT(T, x)
T[x.key] = x
DIRECT-ADDRESS-DELETE(T, x)
T[x.key] = NIL
上述的每一个操作都只需O(1)时间。
对于某些应用,直接寻址表本身就可以存放动态集合中的元素。也就是说,并不把每个元素的关键字及其卫星数据都放在直接寻址表外部的一个对象中,再由表中某个槽的指针指向该对象,而是直接把该对象存放在表的槽中,从而节省了空间。我们使用对象内的一-个特殊关键字来表明该槽为空槽。而且,通常不必存储该对象的关键字属性,因为如果知道一个对象在表中的下标,就可以得到它的关键字。然而,如果不存储关键字,我们就必须有某种方法来确定某个槽是否为空。
散列表
直接寻址技术存在着较大的弊端:如果全域很大,但是分配的有效的关键字集合K相对于U来说可能很小,那个分配给T的绝大部分空间就可能会被浪费掉。
在直接寻址方式下,具有关键字k的元素被放在槽k中。在散列方式下,该元素被放在槽h(k)中,即利用散列函数,由关键字k计算出槽的位置。这里函数h将关键字的全域U映射到散列表T[0…m-1]的槽位上:
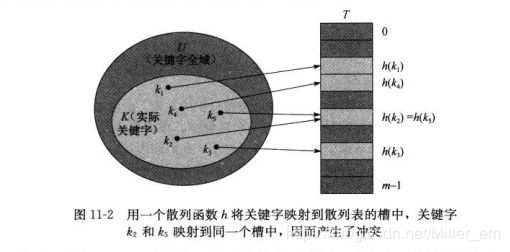
由于两个关键字可能映射到同一个槽中。那么这种情况叫做冲突。下面两种方法可以解决该冲突:链接法和开放寻址法
通过链接法解决冲突
在连接表中,把散列在同一槽中的所有元素都放在一个链表中,槽j中有一个指针,它指向存储所有的散列到j的元素的链表的表头;如果不存在这方的元素,则槽内就是NIL。
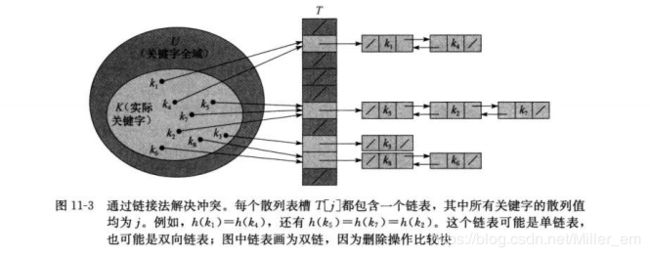
针对链接法散列的分析,有以下两条定理:
**定理11.1:**在简单均匀散列的假设下,对于用链接法解决冲突的散列表,一次不成功查找的平均时间为O(1+α)
**定理11.2:**在简单均匀散列的假设下,对于用链接法解决冲突的散列表,一次成功查找的平均时间为O(1+α)
散列函数
本节将会讨论一些关于如何设计好的散列函数,并介绍三种具体方法。
一个好的散列函数具有以下特点:
满足简单均匀散列假设:每个关键字都被等可能地散列到m个槽位中的任何一个,并与其它关键字已散列到哪个槽位无关。遗憾的是一般无法检查这一条件是否成立,因为很少能知道关键字的概率分布,而且各个关键字可能不是完全独立的。
除法散列法
在用来设计散列表函数的除法散列法中,通过取k除以m的余数,将关键字k映射到m个槽中的某一个上,即散列函数为:
h(k) = k mod m
例如, 如果散列表的大小为m = 12, 所给的关键字为k = 100, 则h(k) = 4.由于只需要做一次出发操作,所以除法散列法是非常快的。使用除数散列法的时候,对于m的选择要慎重。比如m不应该是2的幂。否则如果m = 2p,则h(k)就是k的p个最低位数字(二进制)。除非已经知道关键字的最低p位数的排列是等可能的,否则在设计散列函数时,应该考虑关键字的所有位。一个不太接近2的整数幂的素数是m的一个比较好的选择。
乘法散列法
h(k) = m(kA mod 1)
第一步,用关键字k乘以常数A(0
在乘法散列法中,m的选择不是关键,一般选择m为2的某个次幂。
全域散列表
给定一组散列函数H,每次进行散列时候从H中随机的选择一个散列函数h,使得h独立于要存储的关键字。全域散列函数类的平均性能是比较好的。
开放寻址法
开放定址法是使用某种探测技术在哈希表中形成探测序列,当冲突发生时,沿此序列逐个单元地查找,直到找到空闲单元为止。按照形成探测序列的方法不同,可以将开放定址法分为线性探测法、平方探测法,双哈希函数探测法。
线性探测法
线性探测法是从发生冲突的地址d开始,得到一个探测序列:
d, d+1, d+2, … , m-1, 0, 1, …, d-1 (m为表长)
在每次查找中,若探测到的单元为空闲单元便不再往下探查,把关键字插入该单元。
线性探测法的公式为:
h(k,i) = (h’(k) 十i) mod m(1 <= i <= m-1)
利用线性探查法解决冲突时,会发生聚集现象。当表中第i, i+1, … , i+k位置上已有结点时,一个哈希地址为i, i+1, … , i+k+1的结点都将插入位置i+k+1上。把这种哈希地址不同的结点争夺同一个后继哈希地址的现象成为聚集。这将造成不是同义词的结点也处在同一个探测序列之中,从而增加了探测序列的长度,增加了查找时间。
平方探测法
平方探测法是从发生冲突的地址d开始,得到一个探测序列:
d, d+20, d-20, d+21, d+21, … ,
平方探测法的探测序列跳跃式地散列在整个哈希表中可以减少聚集现象的发生。该方法的缺点是不能够探测到整个哈希地址空间。
双重散列法
双重散列是用于开放寻址法的最好方法之一,因为它所产生的排列具有随机选择排列的许多特性。双重散列采用如下形式的散列函数:
h(k,i) = (h1(k) + ih2 (k) ) mod m
在双重散列中要求h1(k) 与m互素,这样才能发生冲突的同义词地址均匀地分布在整个哈希表中。