统计推断——假设检验中 p 值的含义具体是什么?
「假设检验」,顾名思义,就是通过概率统计的知识来判断一个命题(如「抛掷一枚硬币出现正反面的概率是均匀的」,如「![]() 值大于0.75」)的真伪性。
值大于0.75」)的真伪性。
这个命题便称作「零假设,null hypothesis」,我们通常可以将该命题用数学语言表达出来,比如:「抛掷一枚硬币出现正反面的概率是均匀的」可以定义为「硬币出现正面的概率![]() 为
为![]() ,即
,即![]() 。」这个命题在统计学中通常用
。」这个命题在统计学中通常用![]() 来表示,所以我们需要检验的假设写成:
来表示,所以我们需要检验的假设写成:![]() :
:![]() 。
。
然后问题就来了,在什么情况下,我们认为![]() 这个假设是不正确的呢?我们需要给出一个判断条件,这个判断条件通常有三种给出方式:
这个假设是不正确的呢?我们需要给出一个判断条件,这个判断条件通常有三种给出方式:
1.比
大很多;
2.比
小很多;
3.比
大很多或小很多。
在统计学上,我们将这个判断条件称为「对立假设,alternative hypothesis」,通常用![]() 来表示,以上三种情况可以分别写为:
来表示,以上三种情况可以分别写为:
1.:
;-----------单侧
2.:
;-----------单侧
3.:
。-----------双侧
前两种对立假设下的检验被称为单侧检验,而第三种对立假设下的检验被称为双侧检验。
然而,「对立假设」的条件仍不是很明确,以第一种对立假设![]() :
:![]() 为例,究竟
为例,究竟![]() 偏离
偏离![]() 多远,我们才认为零假设
多远,我们才认为零假设![]() :
:![]() 不成立,而对立假设成立呢?我们下一步要做的,就是要量化这个评判标准。很明显,我们的标准越严格,我们越有可能拒绝
不成立,而对立假设成立呢?我们下一步要做的,就是要量化这个评判标准。很明显,我们的标准越严格,我们越有可能拒绝![]() 而接受
而接受![]() ,在这一过程中,我们可能会犯两种错误:
,在这一过程中,我们可能会犯两种错误:
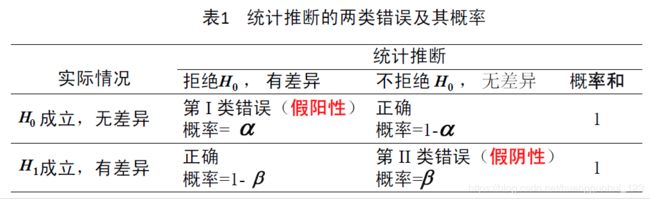
第1类错误:是真的,但是由于我们标准过于严格,把他拒绝掉了;
第2类错误:是假的,但是由于我们标准过于宽松,没有把它拒绝掉;
这两类错误在医学上概括为「假阳性」错误和「假阴性」错误。
:该患者无病。
:该患者异常。
「假阳性」例如把没病说成有病,把无效说成有效。
「假阴性」例如把有病说成没病,把有效说成无效。
虽然我们永远不会知道我们假设检验是否犯了错误,但幸运的是,我们可以知道我们犯这两类错误的概率。在制定评判标准的时候,我们要在犯两类错误的概率之间有所权衡。
我们将犯第1类错误的概率,即「拒绝了一个真的假设」的概率称为「显著性水平,significance level」,通常用字母![]() 表示,即:
表示,即:
本来【该患者是没病的】,但检验之后我们认为【该患者是有病的】;显著性水平即为「被告」![]() 被误诊的概率。通常情况下,我们不希望被误诊,所以我们会在进行假设检验之前,取定一个
被误诊的概率。通常情况下,我们不希望被误诊,所以我们会在进行假设检验之前,取定一个![]() 的值,而且这个值通常比较小。
的值,而且这个值通常比较小。
在一定的![]() 的值的情况下,我们去考察犯第2类错误的概率,即「接受了一个假的假设」的概率,通常用字母
的值的情况下,我们去考察犯第2类错误的概率,即「接受了一个假的假设」的概率,通常用字母![]() 表示,
表示,
显然,我们希望这个概率越小越好,因为这个概率越小,我们的检验能力越厉害。我们用「检验的功效」来刻画我们检验的厉害程度,用![]() 来表示:
来表示:
也就是,在尽量不将【实际无病患者说成有病患者】(第一类错误越小)的情况下,我们越能找出【实际有病却说成无病的患者】,我们这个假设检验的势就越大。即控制两个错误出现的概率(![]() ,
,![]() )都尽量小,但是在实际操作中,给定的
)都尽量小,但是在实际操作中,给定的![]() 小,则
小,则![]() 就大,反之亦然。
就大,反之亦然。
P值的意义
之前说到,当我们进行一个假设检验之前,通常要先选定一个显著性水平,也就是你所能接受的假阳性(无病说有病)的概率。然而,每位医生在这一点上是有分歧的,有的人希望![]() 大一点儿,有的人希望
大一点儿,有的人希望![]() 小一点儿。(
小一点儿。(![]() 越大,意味着检验越严格,我们将无病患者说有病的概率就越大)
越大,意味着检验越严格,我们将无病患者说有病的概率就越大)
在这种情况下,我们就期望回答一个问题:对于面前的这个患者(假设其无病),我们拿到了他的数据,计算其不会误诊(无病说有病)他的最严格的检验水平(![]() ),即最大的
),即最大的![]() 是多少?得到了这个问题的答案,我们就可以轻松完成在任意严格程度上的检验了,如果某位医生所希望的
是多少?得到了这个问题的答案,我们就可以轻松完成在任意严格程度上的检验了,如果某位医生所希望的![]() (实现确定的显著性水平)大于这个值(
(实现确定的显著性水平)大于这个值(![]() ),那么我们就认为患者存在异常,反之亦可。
),那么我们就认为患者存在异常,反之亦可。
如果 ![]() ,,表明“不大可能”犯假阳性错误 (无病说有病),即推翻零假设。
,,表明“不大可能”犯假阳性错误 (无病说有病),即推翻零假设。
如果 ![]() ,,表明“颇有可能”犯假阳性错误 (无病说有病),推翻零假设的风险太大,保持原假设。
,,表明“颇有可能”犯假阳性错误 (无病说有病),推翻零假设的风险太大,保持原假设。
而这个最大的![]() ,就是我们的
,就是我们的![]() 值,即
值,即
所概括的:
假设检验正确(零假设成立)的情况下,得到当前情况乃至更差情况的概率。
【通俗理解】:
在零假设成立的条件(模型)下,当前情况及更差情况发生的概率(![]() )较大,大于我们可以允许的抽样误差范围(显著性水平
)较大,大于我们可以允许的抽样误差范围(显著性水平![]() ),说明在当前假设下,仍有较大可能发生此情况,则保留原假设,拒绝备择假设。
),说明在当前假设下,仍有较大可能发生此情况,则保留原假设,拒绝备择假设。
当前情况及更差情况发生的概率(![]() )较小,远小于我们可以允许的抽样误差范围(显著性水平
)较小,远小于我们可以允许的抽样误差范围(显著性水平![]() ),说明当前假设下,不大可能发生此情况,则拒绝原假设。
),说明当前假设下,不大可能发生此情况,则拒绝原假设。
对于一枚均匀的硬币来说,
投掷20次,得到18次正面是当前情况,
投掷20次,得到18次反面对于硬币的均匀性来说,是同样「差」的情况,
而投掷20次,出现19次正面、出现20次正面,出现19次反面,出现20次正面,对于硬币的均匀性来说,都是比当前情况「更差」的情况。
所以,![]() 值就是将一枚均匀的硬币投掷20次,出现以下情况的概率:
值就是将一枚均匀的硬币投掷20次,出现以下情况的概率:
18次正面,19次正面,20次正面,18次反面,19次反面,20次反面
注意,这是在「双侧检验」的前提下得到的结论,即我们的「对立假设」为通常意义下的「硬币不均匀」,即出现太多的正面与太多的反面是同样不好的情况。
如果我们换一个「对立假设」,采用「单侧检验」的方式,即允许均匀硬币出现更多的反面,即「硬币不均匀」是指「投掷硬币出现了异常多的正面」。「对立假设」意味着,即使我们投掷一枚硬币一亿次都是反面,我们仍旧认为它是「均匀的」。此时,![]() 值就是将一枚均匀的硬币投掷20次,出现以下情况的概率:
值就是将一枚均匀的硬币投掷20次,出现以下情况的概率:
18次正面,19次正面,20次正面
接下来我们通过代码来验证上面的理论。
假设我们投掷一枚硬币20次,结果得到18次正面和2次反面,基于这个结果,我们怀疑这个硬币质地不均匀,落地时正面朝上的可能性更大。
基于以上命题,可以进行验证,我们验证的思路是这样的:我们计算出当质地均匀时,出现这种情况的概率,根据小概率事件的原理,如果我们硬币质地均匀,我们抽到此种情况(18次正面,2次反面)的概率很低,那么我们认为这种情况(18次正面,2次反面)在质地均匀的条件下是很难发生的,我们就有理由认为硬币是不均匀的。
import collections
#模拟每组20次的投掷硬币结果,0表示正面,1表示反面
def RunModel(n): #n为样本单组投掷的次数
sample=np.random.choice(2,n)
counter=collections.Counter(sample)
data=counter[0],counter[1]
return data
#计算每组投掷结果正面和反面差值的绝对值
def testStatistic(data):
heads,tails=data
di=abs(heads-tails)
return di
#模拟1000组的结果
a=[testStatistic(RunModel(20)) for _ in range(1000)]
sorted(a,reverse=True) #对正反面差值出现的次数进行降序处理
输出:
计算比当前情况(18次正面和2次反面)乃至更差情况出现的次数,及出现的概率。
b=sum(1 for x in a if x>=18-2) #计算比当前情况乃至更差情况出现的次数
b/1000输出:
2
0.002
在质地均匀硬币的1000次试验当中,仅有两次出现了比当前情况更极端的现象,出现的概率为0.002,概率极低,我们认为在质地均匀的条件下发生此情况的可能性极低,我们更倾向去相信硬币是不均匀的。