统计学——单因素方差分析

 

概念

 

方差分析：又称变异分析，是英国统计学家R.A.Fisher于1923年提出的一种统计方法，故有时也称为F检验。

 

可简写为ANOVA。用于多组均数 之间的显著性检验。

 

要求：各组观察值服从正态分布或近似正态分布，并且各组之间的方差具有齐性。

 

基本思想：将所有测量值间的总变异按照其变异的来源分解为多个部份，然后进行比较，评价由某种因素所引起的变异是否具有统计学意义。

 

计算方法

 

总变异（Total variation）：全部测量值xij与总均数间μ的差异

组间变异（ between group variation ）：各组的均数μi与总均数μ间的差异

组内变异（within groupvariation )：每组的每个测量值xij与该组均数μi的差异

 

 

 

 

其中，三种变异的关系为：SST = SSB + SSW，DT = DB+ DW

 

例题

 

 

 

有三组人，分别服用了不同的高血压药A，B，C一个月以后，观察每一个人血压下降数：

A组               4             5             7             3             8             5             3                                           μA= 5.00

B组               1             5             3             7             4             2             7             4             1             μB= 3.78

C组               7             8             10           6             9             8                                                          μC= 8.00

我们想要知道A，B，C三个药对于下降血压的效果是否有明显的区别。

 

解题

 

假设：

H0：A，B，C三个药下降血压效果没有区别，即μA= μB= μC

H1：A，B，C三个药下降血压有区别

 

1. 首先我们需要求SST，SSB，SSW

 

求SST之前我们先需要求出A，B，C三组人的平均值：

μ = (xA1+xA2+…+xAn+xB1+xB2+…+xBn+xC1+xC2+…+xCn)

= (4+5+7+3+8+5+3+1+5+3+7+4+2+7+4+1+7+8+10+6+9+8)/22

= 5.32

 

所以SST = (xA1-μ)2+…+(xAn-μ)2+(xB1-μ)2…+(xBn-μ)2+(xC1-μ)2…+(xCn-μ)2

= (4-μ)2+…+(3 -μ)2+(1-μ)2…+(1-μ)2+(7-μ)2…+(8-μ)2

= 139

 

再求SSB = (μA -μ) 2+(μA-μ)2+( μA-μ)2+( μB-μ)2+( μB-μ)2+( μB-μ)2+( μC-μ)2+( μC-μ)2+( μC-μ)2=65.2

 

最后求

SSW = (xA1- μA)2+…+(xAn- μA)2+(xB1-μB)2…+(xBn- μB)2+(xC1-μC)2…+(xCn- μC)2

= (4-5.00)2+…+(3 -5.00)2+(1-3.78)2…+(1-3.78)2+(7-8.00)2…+(8 -8.00)2

= 73.6

 

根据性质SST = SSW + SSB，所以这三个只要求出其它两个，另外一个用等式SST= SSW + SSB即可求出。

 

2. 我们求自由度：DT，DB，DW。

 

我们知道样本总共有22个，而且我们知道样本总体的值，所以我们只需要知道其中21个样本，剩下的1个就可以的出来，所以总体自由度DT= 22-1 = 21

 

因为我们有3组，我们只需要知道其中的两组，另外一组也可以的出来，所以组间自由度DB= 3-2 = 2

 

第一组有7个样本，我们只需要知道其中的6个，剩下的一个可以的出来，所以第一组的自由度DW1= (7-1) = 6，同理，第二三组的也可以的出来，所以总的组内自由度DW= (7-1) + (9-1) +(6-1) = 19

 

同理，我们有性质DT = DB + DW，所以我们只要知道其中两个自由度，剩下的一个可以由公式得出。

 

3. 最后我们求F，F的公式为F = (SSB/DB) / (SSW/DW) =(65.2/2) / (73.6/19) = 8.42，且自由度为F(2,19)

 

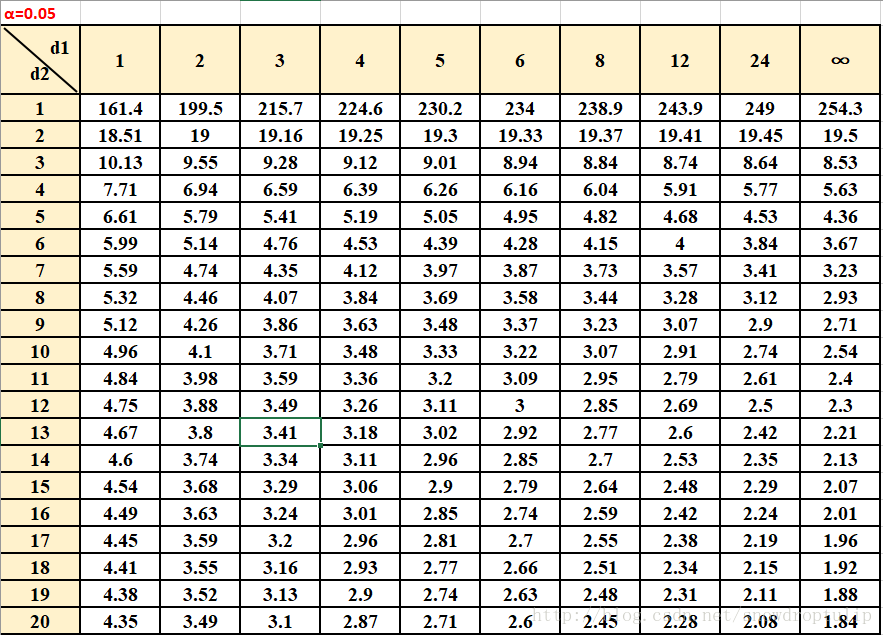
此时我们α=0.05的F分布表如下图，我们看到自由度为2和19时，置信度为95%的值为3.52，而此时我们的值为8.42，远超过3.52，所以我们接受H0的概率小于0.05，所以拒绝H0假设，接受H1，即A，B，C三个药的效果有明显的不同

R语言实现

 

anova = function(x){
  
  x_mean = sapply(x,mean)
  total_mean = mean(unlist(x))
  
  sst = sum((unlist(x)-total_mean)^2)
  
  ssw = 0
  for(i in 1:length(x)){
    w = sum((x[[i]]-x_mean[i])^2)
    ssw = ssw + w
  }
  
  ssb = 0
  for(i in 1:length(x)){
    b = length(x[[i]])*((x_mean[i]-total_mean)^2)
    ssb = ssb + b
  }
  
  Nt = length(unlist(x))-1 # 总自由度
  Nb = length(x)-1 # 组间自由度
  Nw = Nt - Nb 
  
  f = (ssb/Nb)/(ssw/Nw)
  
  result = c(sst,ssb,ssw,Nt,Nb,Nw,f)
  names(result)= c('sst','ssb','ssw','Nt','Nb','Nw','f')
  
  return(result)
  
}

x1 = c(4,5,7,3,8,5,3)
x2 = c(1,5,3,7,4,2,7,4,1)
x3 = c(7,8,10,6,9,8)
x = list(x1,x2,x3)

f = anova(x)

最后得出f为：