Datawhale计算机视觉基础-图像处理(下)-Task02 LBP特征描述算子-人脸检测
目录
- 1 简介
- 2 算法原理
- 2.1 LBP原理介绍
- 2.2 圆形LBP算子
- 2.3 LBP旋转不变性及等价模式
- 2.4 人脸检测流程
- 3 基于OpenCV的实现
1 简介
LBP指局部二值模式(Local Binary Pattern),是一种用来描述图像局部特征的算子,具有灰度不变性和旋转不变性等显著优点。LBP常应用于人脸识别和目标检测中,在OpenCV中有使用LBP特征进行人脸识别的接口,也有用LBP特征训练目标检测分类器的方法,OpenCV实现了LBP特征的计算,但没有提供一个单独的计算LBP特征的接口。也就是说OpenCV中使用了LBP算法,但是没有提供函数接口。
2 算法原理
2.1 LBP原理介绍
LBP特征用图像的局部领域的联合分布 T T T 来描述图像的纹理特征,如果假设局部邻域中像素个数为 P ( P > 1 ) P(P >1) P(P>1),那么纹理特征的联合分布 T T T 可以表述成:
T = t ( g c , g 0 , … , g p − 1 ) p = 0 , … , P − 1 (2-1) T=t\left(g_{c}, g_{0}, \ldots, g_{p-1}\right) \quad p=0, \ldots, P-1\tag{2-1} T=t(gc,g0,…,gp−1)p=0,…,P−1(2-1)
其中, g c g_c gc 表示相应局部邻域的中心像素的灰度值, g p g_p gp 表示以中心像素圆心,以R为半径的圆上的像素的灰度值。
假设中心像素和局部邻域像素相互独立,那么这里可以将上面定义式写成如下形式:
T = t ( g c , g 0 − g c , … , g p − 1 − g c ) p = 0 , … , P − 1 ≈ t ( g c ) t ( g 0 − g c , … , g p − 1 − g c ) (2-2) \begin{aligned} T &=t\left(g_{c}, g_{0}-g_{c}, \ldots, g_{p-1}-g_{c}\right) \quad p=0, \ldots, P-1 \ \\ & \approx t\left(g_{c}\right) t\left(g_{0}-g_{c}, \ldots, g_{p-1}-g_{c}\right) \end{aligned}\tag{2-2} T=t(gc,g0−gc,…,gp−1−gc)p=0,…,P−1 ≈t(gc)t(g0−gc,…,gp−1−gc)(2-2)
其中 t ( g c ) t(g_c) t(gc)决定了局部区域的整体亮度,对于纹理特征,可以忽略这一项,最终得到:
T ≈ t ( g 0 − g c , … , g p − 1 − g c ) p = 0 , … , P − 1 (2-3) T \approx t\left(g_{0}-g_{c}, \ldots, g_{p-1}-g_{c}\right) \quad p=0, \ldots, P-1\tag{2-3} T≈t(g0−gc,…,gp−1−gc)p=0,…,P−1(2-3)
上式说明,将纹理特征定义为邻域像素和中心像素的差的联合分布函数,因为 g p − g c g_p − g_c gp−gc是基本不受亮度均值影响的,所以从上式可以看出,此时统计量T 是一个跟亮度均值,即灰度级无关的值。
最后定义特征函数如下:
T ≈ t ( s ( g 0 − g c ) , … , s ( g p − 1 − g c ) ) p = 0 , … , P − 1 s ( x ) = { 1 , x ≥ 0 0 , x < 0 \begin{array}{l} T \approx t\left(s\left(g_{0}-g_{c}\right), \ldots, s\left(g_{p-1}-g_{c}\right)\right) p=0, \ldots, P-1 \\\\ s(x)=\left\{\begin{array}{l} 1, x \geq 0 \\ 0, x<0 \end{array}\right. \end{array} T≈t(s(g0−gc),…,s(gp−1−gc))p=0,…,P−1s(x)={1,x≥00,x<0
定义灰度级不变LBP为:
L B P P , R = ∑ p = 0 P − 1 s ( g p − g c ) 2 p (2-5) L B P_{P, R}=\sum_{p=0}^{P-1} s\left(g_{p}-g_{c}\right) 2^{p}\tag{2-5} LBPP,R=p=0∑P−1s(gp−gc)2p(2-5)
即二进制编码公式。
通俗解释:
原始的LBP算子定义在像素 33 33 33的邻域内,以邻域中心像素为阈值,相邻的8个像素的灰度值与邻域中心的像素值进行比较,若周围像素大于中心像素值,则该像素点的位置被标记为1,否则为0。这样, 33 33 33邻域内的8个点经过比较可产生8为二进制数,将这8位二进制数依次排列形成一个二进制数字,这个二进制数字就是中心像素的LBP值,LBP值共有28种可能,因此LBP值有256种可能。中心像素的LBP值反映了该像素周围区域的纹理信息。
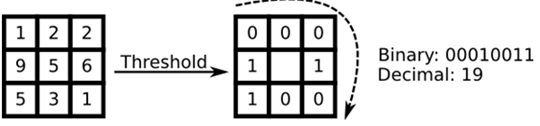
2.2 圆形LBP算子
基本的 LBP算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域,这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征,并达到灰度级和旋转不变性的要求,Ojala等对 LBP算子进行了改进,将 3×3邻域扩展到任意邻域,并用圆形邻域代替了正方形邻域,改进后的 LBP算子允许在半径为 R的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子,表示为 L B P P R LBP^{R}_P LBPPR;

对于给定中心点 ( x c , y c ) (x_c,y_c) (xc,yc),其邻域像素位置为 ( x p , y p ) (x_p,y_p) (xp,yp), p ∈ P p∈P p∈P,其采样点 ( x p , y p ) (x_p,y_p) (xp,yp)用如下公式计算:
x p = x c + Rcos ( 2 π p P ) y p = y c + Rsin ( 2 π p P ) (2-6) \begin{array}{l} x_{p}=x_{c}+\operatorname{Rcos}\left(\frac{2 \pi p}{P}\right) \ y_{p}=y_{c}+\operatorname{Rsin}\left(\frac{2 \pi p}{P}\right) \end{array}\tag{2-6} xp=xc+Rcos(P2πp) yp=yc+Rsin(P2πp)(2-6)
R是采样半径,p是第p个采样点,P是采样数目。如果近邻点不在整数位置上,就需要进行插值运算,可以参考这篇博客 OpenCV框架下的插值算法
2.3 LBP旋转不变性及等价模式
LPB特征是灰度不变,但不是旋转不变的,同一幅图像,进行旋转以后,其特征将会有很大的差别,影响匹配的精度。Ojala在LBP算法上,进行改进,实现了具有旋转不变性的LPB的特征。
实现方法:不断旋转圆形邻域得到一系列初始定义的LPB值,取最小值作为该邻域的值。
L B P P R r i = min ( R O R ( L B P P , R r i , i ) ∣ i = 0 , 1 , … , P − 1 ) (2-7) L B P_{P R}^{ri}=\min \left(R O R\left(L B P_{P, R}^{ri}, i\right) | i=0,1, \ldots, P-1\right)\tag{2-7} LBPPRri=min(ROR(LBPP,Rri,i)∣i=0,1,…,P−1)(2-7)
其中 L B P P R r i L B P_{P R}^{ri} LBPPRri表示具有旋转不变性的LBP特征。 R O R ( x , i ) ROR(x, i) ROR(x,i)为旋转函数,表示将 x x x右循环 i i i位。
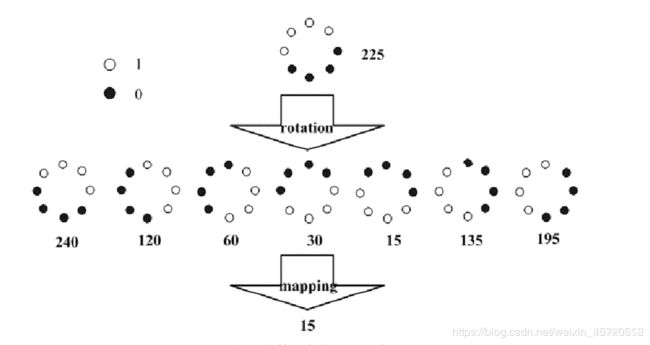
等价模式:
一个LBP算子可以产生不同的二进制模式,对于 L B P p R LBP^{R}_p LBPpR将会产生 2 p 2^p 2p种模式。比如 7 ∗ 7 7*7 7∗7邻域内有 2 36 2^{36} 236种模式。如此多的二值模式对于信息的提取和识别都是不利的。
Ojala等认为,在实际图像中,绝大多数LPB模式最多只包含两次从1到0或从0到1的跳变。
等价模式:当某个局部二进制模式所对应的循环二进制数从0到1或从1到0最多有两次跳变时,该局部二进制模式所对应的二进制就称为一个等价模式。
比如:00000000,11111111,11110010,10111111都是等价模式。
检查某种模式是否是等价模式: U ( G p ) = ∣ s ( g p − 1 − g c ) − s ( g 0 − g c ) ∣ + ∑ p = 1 P − 1 ∣ s ( g p − g c ) − s ( g P − 1 − g c ) ∣ (2-8) U\left(G_{p}\right)=\left|s\left(g_{p_{-1}}-g_{c}\right)-s\left(g_{0}-g_{c}\right)\right|+\sum_{p=1}^{P_{-1}}\left|s\left(g_{p}-g_{c}\right)-s\left(g_{P-1}-g_{c}\right)\right|\tag{2-8} U(Gp)=∣s(gp−1−gc)−s(g0−gc)∣+p=1∑P−1∣s(gp−gc)−s(gP−1−gc)∣(2-8)
将其和其移动一位后的二进制模式按位相减。并绝对值求和。若U ( G p ) \left(G_{p}\right) (Gp) 小于等于2,则为等价模式。
**混合模式:**除了等价模式之外的称为混合模式。
改进后的LPB模式数由2 p ^{p} p(p为邻域集内的采集点数 ) 降维为 p ∗ ( p − 1 ) + 2 p*(p-1)+2 p∗(p−1)+2 。维数减少,可以降低高频噪声的影响。Ojala认为等价模式占总模式中的绝大数。图2.4 ( a ), ( b ), ( c )等价模式分别占88%,93%和76%。

可以通过低通滤波的方法来增强等价模式所占的比例。图2.4( c )经过高斯滤波后,其等价模式所占比可以增加到90%。
2.4 人脸检测流程
人脸检测过程采用多尺度滑窗搜索方式,每个尺度通过一定步长截取大小为20x20的窗口,然后将窗口放到分类器中进行是不是人脸的判决,如果是人脸则该窗口通过所有分类器;反之,会在某一级分类器被排除。
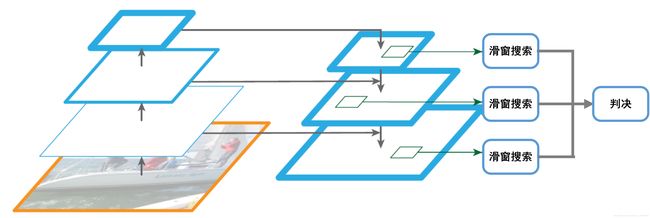
3 基于OpenCV的实现
python
使用OpenCV的LBP预训练模型
将haarcascade_frontalface_default.xml下载至本地以方便调用,下载链接:
https://github.com/opencv/opencv/blob/master/data/lbpcascades/lbpcascade_frontalface_improved.xml
#coding:utf-8
import cv2 as cv
# 读取原始图像
img= cv.imread('*.png')
#face_detect = cv2.CascadeClassifier('haarcascade_frontalface_default.xml')
face_detect = cv.CascadeClassifier("lbpcascade_frontalface_improved.xml")
# 检测人脸
# 灰度处理
gray = cv.cvtColor(img, code=cv.COLOR_BGR2GRAY)
# 检查人脸 按照1.1倍放到 周围最小像素为5
face_zone = face_detect.detectMultiScale(gray, scaleFactor = 2, minNeighbors = 2) # maxSize = (55,55)
print ('识别人脸的信息:\n',face_zone)
# 绘制矩形和圆形检测人脸
for x, y, w, h in face_zone:
# 绘制矩形人脸区域
cv.rectangle(img, pt1 = (x, y), pt2 = (x+w, y+h), color = [0,0,255], thickness=2)
# 绘制圆形人脸区域 radius表示半径
cv.circle(img, center = (x + w//2, y + h//2), radius = w//2, color = [0,255,0], thickness = 2)
# 设置图片可以手动调节大小
cv.namedWindow("Easmount-CSDN", 0)
# 显示图片
cv.imshow("Easmount-CSDN", img)
# 等待显示 设置任意键退出程序
cv.waitKey(0)
cv.destroyAllWindows()

