lecture02 : Word Vectors 2 and Word Senses

lecture02 : Word Vectors 2 and Word Senses

1. word vertor and word2vec

word2vec基本在lecture01，这里写一些补充的东西。

Word2vec maximizes objective function by putting similar words nearby in space5

word2vec 将相似的词更加相近。

Optimization：

• Gradient Descent：在全部样本上
• Stochastic Gradient Descent：对全部样本进行随机采样，在采样的样本上计算梯度。在每次更新时用1个样本。

why two vectores?

Easier optimization. Average both at the end

why not capture co-occurrence counts directly

With a co-occurrence matrix X，有两种方法，windows和document。

问题：

1. 随着词汇量的增加而增加
2. 非常高维的:需要大量的存储空间
3. 后续的分类模型存在稀疏性问题

会导致模型不那么健壮。

解决方法

1. 对X进行降维，比如SVD。但会有有的词太频繁了，解决方法有（1）$min(x，t)t约等于100$；（2）全部忽略; Ramped windows that count closer words more；Use Pearson correlations instead of counts, then set negative values to 0；

Encoding meaning in vector differences

Log-bilinear model:$w_i\ast w_j=\log P(i|j)$

with vector differences $w_x\ast (w_a-w_b)=\log \frac{P(x|a)}{P(x|b)}$

2. GloVe : Combining the best of both

$$J=\sum _{i,j=1}^{V}f(X_{ij})(w_i^T{\tilde{w}}_j+b_i+{\tilde{b}}_j-\log X_{ij}{)}^2$$

优点：

• Fast training
• Scalable to huge corpora
• Good performance even with small corpus and small vectors

2.1 和之前的模型进行比较

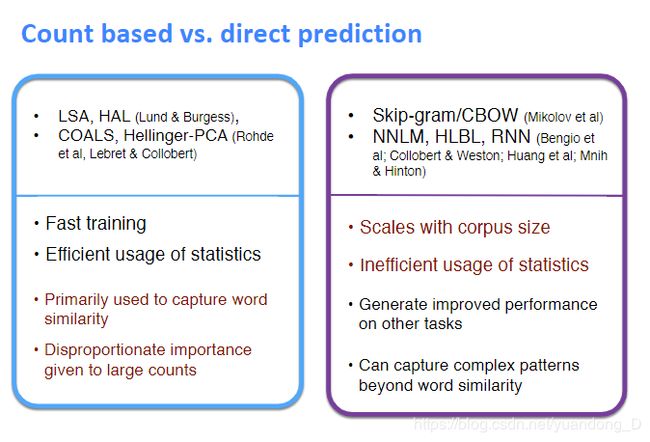
到目前为止有两种模型来获取word emdeddings。第一种是基于计数的（LSA、HAL）。虽然这些方法有效地利用了全局统计信息，但它们主要用于捕获词的相似性，而在进行词的类比、分离次优向量空间结构(indicating a sub-optimal vector space structure)等任务时表现较差。另一种是基于窗口的(skpi-gram and CBOW)，虽然有捕捉语义的能力但没有利用全局的共现信息。

Glove由一个加权最小二乘组成，训练共现信息，有效利用统计信息。

2.2 Co-occurrence Matrix

$X_{ij}$代表单词j出现在单词i上下文的概率。$X_i={\sum }_k{X}_{ik}$是所有词出现在词i上下文的总数。$P_{ij}=P(w_j|w_i)=\frac{X_{ij}}{X_i}$代表j出现在i上下文的概率。

计算共现矩阵对于大规模文本需要大量计算，但是是一次的前期成本。

2.3 Least Squares Objective

在skip-gram模型种我们用softmax计算概率。然后计算交叉熵

$$J=-\sum _{i\in corpus}\sum _{j\in context(i)}\log Q_{ij}$$

但是相同的i和j可以共同出现多次。可以将他们合在一起提高效率。

$$J=-\sum _{i=1}^W\sum _{j=1}^W{X}_{ij}\log Q_{ij}$$

交叉熵损失的一个显著缺点是它要求分布Q被标准化，涉及到整个词汇量的昂贵的求和操作。所以我们使用最小二乘。

$$\hat{J}=\sum _{i=1}^W\sum _{j=1}^W{X}_{ij}({\hat{P}}_{ij}-{\hat{Q}}_{ij}{)}^2$$

where ${\hat{P}}_{ij}=X_{ij}and{\hat{Q}}_i=exp({\hat{u}}_j^T{\hat{v}}_i)$，但是产生一个问题是X_{ij}的值经常非常大使得优化很困难，所以将$\hat{P}and\hat{Q}$对数化。

$$\begin{gathered} \hat{J}=\sum _{i=1}^W\sum _{j=1}^W{X}_i(\log {\hat{P}}_{ij}-\log {\hat{Q}}_{ij}{)}^2 \\ =\sum _{i=1}^W\sum _{j=1}^W{X}_i({\hat{u}}_j^T{\hat{v}}_i-\log X_{ij}{)}^2 \end{gathered}$$

然后观察到权重因子$X_i$不是最优的所以：

$$\hat{J}=\sum _{i=1}^W\sum _{j=1}^{W}f(X_{ij})({\hat{u}}_j^T{\hat{v}}_i-\log X_{ij}{)}^2$$

2.4 conclusion

Glove模型只对共现矩阵的非零元素进行训练，有效的利用的全局统计信息。在相同条件下比word2vec表现的更加出色。

3. How to evaluate word vector?

3.1 Intrinsic vs extrinsic

Intrinsic:

• 对特定的任务评估（比如类比比较）
• Fast to compute
• Helps to understand that system
• Not clear if really helpful unless correlation to real task is established

Extrinsic

• Evaluation on a real task
• Can take a long time to compute accuracy
• Unclear if the subsystem is the problem or its interaction or other subsystems
• If replacing exactly one subsystem with another improves accuracy --> Winning!

3.2 Intrinsic word vector evaluation

方法一:Word Vector Analogies

Word Vector Analogies：Syntactiv and Semantic

$$a:b::c:?$$

$$d=\underset{i}{\mathrm{argmax}}\frac{(x_b-x_a+x_c{)}^T{x}_i}{||x_b-x_a+x_c||}$$

存在的问题：如果信息是存在的但不是线性的呢

根据Intrinsic分析超参数得到：

• 最好是300维左右
• asymmetric context (only words to the left)不对称上下文 不是很好。
• window size of 8 is good for Glove
• Performance is heavily dependent on the model used for word embedding
• Performance increases with larger corpus sizes
• Performance is lower for extremely low dimensional word vectors

方法二:Correlation Evaluation

Word vector distances and their correlation with human judgments

Example dataset: WordSim353

3.3 Word senses and word sense ambiguity

每个词都有很多种意思，一个词向量是否捕获了所有的这些意思呢？有如下解决方法：

Improving Word Representations Via Global Context And Multiple Word Prototypes

Idea: Cluster word windows around words, retrain with each word assigned to multiple different clusters bank1, bank2.

Linear Algebraic Structure of Word Senses, with Applications to Polysemy

$v_{p}ike={\alpha }_1{v}_{pik{e}_1}+{\alpha }_2{v}_{pik{e}_2}+...$

${\alpha }_1$是频率

3.4 Extrinsic word vector evaluation

Extrinsic evaluation of word vectors: All subsequent tasks in this class,比如命名实体识别

3.4.1 Problem Formulation

对于NLP的分类问题可以公式化为：

$$\{x^{(i)},y^{(i)}{\}}_1^N$$

与一般问题不同的是，NLP提出了word embedding再训练的思想。

3.4.2 Retraining Word Vectors

Implementation Tip:Word vector retraining should be considered for large training datasets. For small datasets, retraining word vectors will likely worsen performance

如果我们使用外部任务对单词向量进行再训练，我们需要确保训练集足够大，能够覆盖词汇表中的大多数单词。如果训练数据集很小，就不应该对字向量进行再训练。如果训练集很大，再训练可以提高效率。

3.4.3 Softmax Classification and Regularization

在N个样本点上：

$$\sum _{i=1}^N\log (\frac{exp(W_{k(i)}x)}{{\sum }_{c=1}^{C}exp(W_c{x}^{(i)})})$$

$k(i)$是返回$x^{(i)}$样本的正确索引值，划分为C类则需要更新的参数为$C\ast d+|V|\ast d$

$$\sum _{i=1}^N\log (\frac{exp(W_{k(i)}x)}{{\sum }_{c=1}^{C}exp(W_c{x}^{(i)})})+\lambda \sum _{k=1}^{C\ast d+|V|\ast d}{\theta }_k^2$$

3.4.4 Window Classification

在大多数情况下，我们倾向于使用单词序列作为模型的输入。

参考资料

1. slides
2. note
3. vedio