模糊算法-数据分类/kmean/fcm_matlab实现
文章目录
- 一、需求分析
- 二、概要设计
- 三、详细设计(代码)
- 四、实验结果总结
一、需求分析
本实验为了解和测试模糊算法并在实际背景下进行应用。
1、 寻找合适的具有实际意义的数据集。
2、 根据数据集进行matlab自带的kmeans函数和fcm函数进行分类与分析。
3、 自己设计算法myKmeans函数对数据集进行分类。
数据集1:威斯康星州乳腺癌数据集
原因:目前癌症的初步检测还是主要依靠医生的经验判断,为了提高医生的工作效率,以及减少医生的经验判断失误,所有希望计算机协助医生进行判断。
目标:根据已有的对乳腺癌的特征的分类,判断患者的乳腺癌是属于良性还是恶性,进一步帮助患者的治疗。
数据集2:胸外科数据集
原因:目前肺癌治疗主要肺切除术虽然已经成熟,但是患者是否该接受手术还是应该慎重的评定。
目标:根据已有的数据的特征的分类,判断患者是否应该接受手术治疗,有无成功率。
二、概要设计
myKmeans函数
对于详细设计中的代码2,代码中有详细的注释。
输入:【数据集 ,聚类个数k】
数据集为m*n m个元素,含n维特征变量
1、 选择k个初始的中心点,随机生成 u[1]…u[k]
采用每行的最大值减去(最大最小的差值乘上随机数) 保证初始化的中心值在最大值与最小值之间
2、 对于x[1]…x[n](matlab数组从1开始)分别与u[1]…u[k]比较,假定与u[i]距离最短,就标记为i类
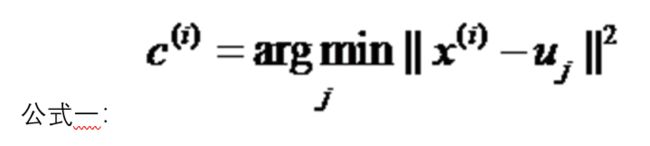
3、 对于所有标记为第i个类别的点,重新计算u[i]={所有标记为i的样本的每个特征的均值}
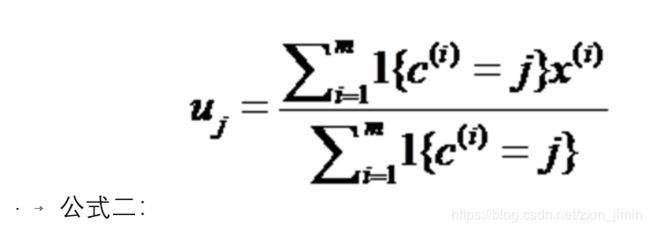
4、 重复第2、3步,直到所有u[i]值的变化小于给定的阈值或达到最大迭代次数
输出:分类中心u(1)…u(k)
分类类别re(1)…re(k)
myfcm函数分析
对于详细设计中的代码2,代码中有详细的注释。
输入:【数据集 ,聚类个数k】
数据集为m*n m个元素,含n维特征变量

输出:分类中心u(1)…u(k)
分类类别re(1)…re(k)
数据集1:
参考:https://www.cnblogs.com/tiandsp/archive/2013/04/24/3040883.html
数据集下载地址:http://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Original)
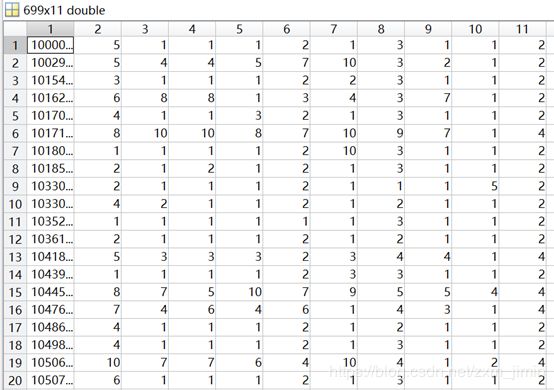
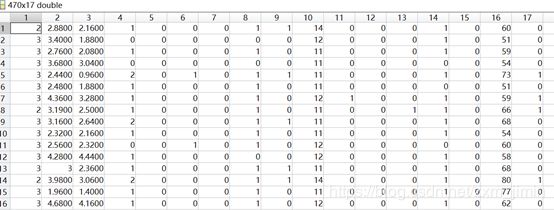
选用的数据来类型为:Breast Cancer Wisconsin (Original) Data Set,中文名称为:威斯康星州乳腺癌数据集。这些数据来源美国威斯康星大学医院的临床病例报告,每条数据具有11个属性。下载下来的数据文件格式为“.data”。
部分截图:
属性值解释:
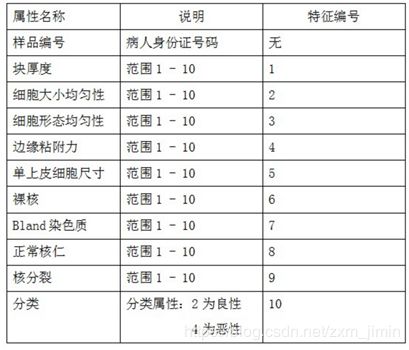
故在设计中从下标2取到下标9的数据作为特征属性,下标10的数据作为分类的类别。
数据集2:
下载地址:http://archive.ics.uci.edu/ml/datasets/Thoracic+Surgery+Data
胸外科数据数据集,该数据致力于与肺癌患者术后预期寿命相关的分类问题:1级 - 术后1年内死亡,2级 - 生存。
转换为txt格式,并对其中一些数据进行修改,修改为数字类型方便分类。
属性信息:
-
DGN:诊断 - 特定组合的ICD-10代码用于原发性和继发性以及多种肿瘤(DGN3,DGN2,DGN4,DGN6,DGN5,DGN8,DGN1)
-
PRE4:强制肺活量 - FVC(数字)
-
PRE5:在强制到期的第一秒结束时呼出的音量 - FEV1(数字)
-
PRE6:性能状态 - Zubrod量程(PRZ2,PRZ1,PRZ0)
-
PRE7:手术前疼痛(T,F)
-
PRE8:手术前咯血(T,F)
-
PRE9:术前呼吸困难(T,F)
-
PRE10:手术前咳嗽(T,F)
-
PRE11:手术前的虚弱(T,F)
-
PRE14:T临床TNM - 原始肿瘤的大小,从OC11(最小)到OC14(最大)(OC11,OC14,OC12,OC13)
-
PRE17:2型糖尿病 - 糖尿病(T,F)
-
PRE19:MI长达6个月(T,F)
-
PRE25:PAD - 外周动脉疾病(T,F)
-
PRE30:吸烟(T,F)
-
PRE32:哮喘(T,F)
16.年龄:手术年龄(数字)
17.风险1Y:1年生存期 - (T)死亡时的rue值(T,F)
三、详细设计(代码)
代码1:
main.m (实现matlab自带的kmeans与fcm方法)
clc;clear;
%测试数据中总共683条,其中良性共444条,恶性共239条:
%load('matlab.mat')%加载测试数据
data=load('breast-cancer-wisconsin.data');%加载测试数据
%load('test.txt')%加载测试数据
%[f1,f2,f3,f4,f5] = textread('test.txt' , '%f%f%f%f%f');
N0 =1 ; %从多少列开始的数据进行预测分类
N1 = size(data,1);%所有数据的行数
data=data(N0:N1,:);%只选取需要测试的数据
data1=data(:,[2,3,4,5,6,7,8,9]);
%%
% [2,4,7,9] 2:size(data,2)-1
opts = statset('Display','final');%控制选项
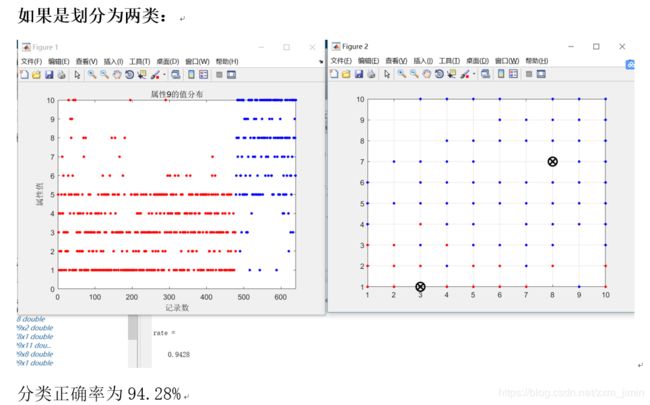
[idx,ctrs,result,D] = kmeans(data1,2,... %data1为要分类的数据,2为分类的类别数,本文只有2类
'Distance','city',... %选择的距离的计算方式
'Options',opts); % 控制选项,参考matlab帮助
%%
m=size(idx,1);
totalSum = 0 ;%总的正确率
t=data(:,1);
for i = 1 : m
if(idx(i,1)==1)
t(i,1)=4;
else
t(i,1)=2;
end
end
d2 = data(:,11);%提取原始数据中属于第1类的数据的最后一列
%t=[data(:,size(data,2)),idx(:,1)];%把测试数据最后一列,也就是分类属性 和 分类结果取出来:列 + 列
for i = 1 : m
if(t(i,1)==d2(i,1))
totalSum=totalSum+1;
end
end
size(t,1)%总数
totalSum
rate = totalSum/size(t,1)%良性的个数
%%
figure(1);
x1 =1;%第x1个属性
x2 =1 ;%第x2个属性
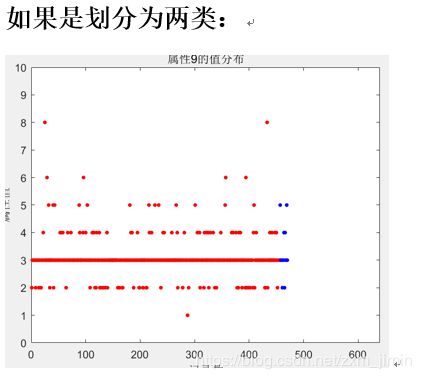
plot(1:sum(idx==1),data1(idx==1,x1),'r.','MarkerSize',12);
hold on ;
plot(sum(idx==1)+1:sum(idx==1)+sum(idx==2),data1(idx==2,x1),'b.','MarkerSize',12);
xlabel('记录数');
ylabel('属性值');
title('属性9的值分布');
axis([0 640 0 10])
figure(2);
%plot3(data1(:,1),data1(:,2),data1(:,3),'r.','MarkerSize',12)
plot(data1(idx==1,1),data1(idx==1,2),'r.','MarkerSize',12)
hold on
plot(data1(idx==2,1),data1(idx==2,2),'b.','MarkerSize',12)
plot(ctrs(:,1),ctrs(:,2),'kx',...
'MarkerSize',12,'LineWidth',2)
plot(ctrs(:,1),ctrs(:,2),'ko',...
'MarkerSize',12,'LineWidth',2)
%legend('Cluster 1','Cluster 2','Centroids','Location','NW')
grid on;%表示在画图的时候添加网格线
%%
data1=data(:,[2,3,4,5,6,7,8,9]);
figure(3);
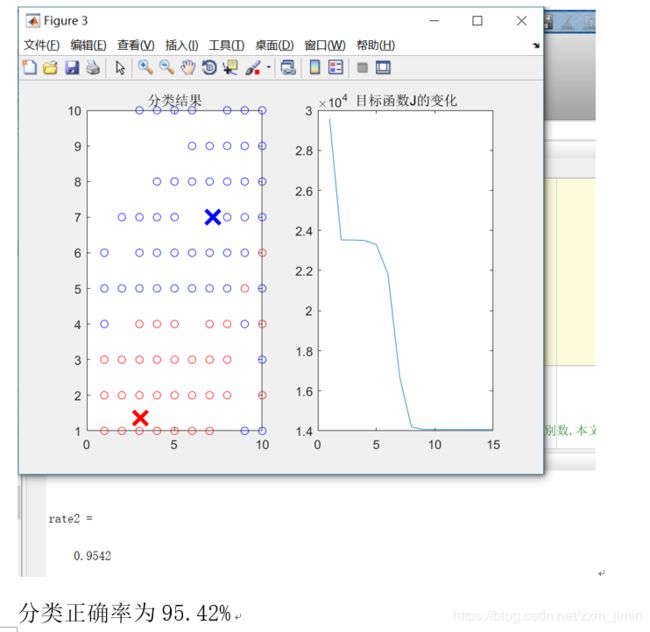
[center,U,obj_fcn] = fcm(data1,2);
subplot(1,2,1);
plot(data1(:,1), data1(:,2),'o');
hold on;
maxU = max(U);
% Find the data points with highest grade of membership in cluster 1
index1 = find(U(1,:) == maxU);
% Find the data points with highest grade of membership in cluster 2
index2 = find(U(2,:) == maxU);
plot(data1(index1,1),data1(index1,2),'ob');
plot(data1(index2,1),data1(index2,2),'or');
% Plot the cluster centers
plot(center(1,1),center(1,2),'xb','MarkerSize',15,'LineWidth',3)
plot(center(2,1),center(2,2),'xr','MarkerSize',15,'LineWidth',3)
title('分类结果')
subplot(1,2,2);
plot(obj_fcn)
title('目标函数J的变化')
hold off;
%%
U=U';
m=size(U,1);
n=size(U,2);
for i = 1 : m
for i = 1 : n
[p , index] = max(U,[],2 ) ;
end
end
totalSum2 = 0 ;%总的正确率
t=data(:,1);
for i = 1 : m
if(index(i,1)==1)
t(i,1)=4;
else
t(i,1)=2;
end
end
d2 = data(:,11);%提取原始数据中属于第1类的数据的最后一列
%t=[data(:,size(data,2)),idx(:,1)];%把测试数据最后一列,也就是分类属性 和 分类结果取出来:列 + 列
for i = 1 : m
if(t(i,1)==d2(i,1))
totalSum2=totalSum2+1;
end
end
size(t,1)%总数
totalSum2
rate2 = totalSum2/size(t,1)%良性的个数
代码2:
myKmeans.m (实现自己的K-means算法)
%N是数据一共分多少类
%data是输入的不带分类标号的数据
%u是每一类的中心
%re是返回的带分类标号的数据
function [u re]=myKMeans(x,k)
%%
[m n]=size(x); %m是数据个数,n是数据维数
%% 选择k个初始中心点,随机生成
[m n]=size(x); %m是数据个数,n是数据维数
ma=zeros(n); %每一维最大的数
mi=zeros(n); %每一维最小的数
u=zeros(k,n); %随机初始化,最终迭代到每一类的中心位置
for i=1:n
ma(i)=max(x(:,i)); %每一维最大的数
mi(i)=min(x(:,i)); %每一维最小的数
for j=1:k
u(j,i)=ma(i)+(mi(i)-ma(i))*rand(); %随机初始化,不过还是在每一维[min max]中初始化好些
end
end
%% 分类 更新中心点
while 1
pre_u=u; %上一次求得的中心位置
for i=1:k
tmp{i}=[]; % 公式一中的x(i)-uj,为公式一实现做准备
for j=1:m
tmp{i}=[tmp{i};x(j,:)-u(i,:)];%tmp存放到u{i}的距离 但是是3个维度的
end
end
quan=zeros(m,k);%全为0
for i=1:m %公式一的实现
c=[];
for j=1:k
c=[c norm(tmp{j}(i,:))];%如果A为矩阵 n=norm(A) 返回A的最大奇异值,即max(svd(A))
%第i行的所有列
%取距离那个中心点{j}比较近 c存放到u{i}的距离(比较好比较的版本)一个维度
end
[junk index]=min(c);%找到距离中心点最小的值
quan(i,index)=1;%分类矩阵 0,1
end
for i=1:k %公式二的实现
for j=1:n
u(i,j)=sum(quan(:,i).*x(:,j))/sum(quan(:,i));%属于这个类别的
end
end
if norm(pre_u-u)<0.1 %不断迭代直到位置不再变化
break;
end
end
%% 标记数据
re=[];
for i=1:m
tmp=[];
for j=1:k
tmp=[tmp norm(x(i,:)-u(j,:))];
end
[junk index]=min(tmp);
re=[re;x(i,:) index];
end
myfcm.m
function [R, V,objFcn] = myfcm(data, k)
%%
T = 100;%默认迭代次数为100
epsm = 1.0e-6; %默认收敛精度
m = 2; %默认模糊系数值为2
%%
[n, s] = size(data);
% 初始化隶属度矩阵U(0),并归一化
U0 = rand(k, n);
temp = sum(U0,1);
for i=1:n
U0(:,i) = U0(:,i)./temp(i);
end
iter = 0;
V(k,s) = 0; R(k,n) = 0; distance(k,n) = 0;
%%
while( itertest_my.m(实现myKmeans,myfcm的分类)
clc;clear;
%测试数据中总共683条,其中良性共444条,恶性共239条:
%load('matlab.mat')%加载测试数据
data=load('breast-cancer-wisconsin.data');%加载测试数据
%load('test.txt')%加载测试数据
%[f1,f2,f3,f4,f5] = textread('test.txt' , '%f%f%f%f%f');
N0 =1 ; %从多少列开始的数据进行预测分类
N1 = size(data,1);%所有数据的行数
data=data(N0:N1,:);%只选取需要测试的数据
data1=data(:,[2,3,4,5,6,7,8,9]);
% [2,4,7,9] 2:size(data,2)-1
%%
% opts = statset('Display','final');%控制选项
% [idx,ctrs,result,D] = kmeans(data1,2,... %data1为要分类的数据,2为分类的类别数,本文只有2类
% 'Distance','city',... %选择的距离的计算方式
% 'Options',opts); % 控制选项,参考matlab帮助
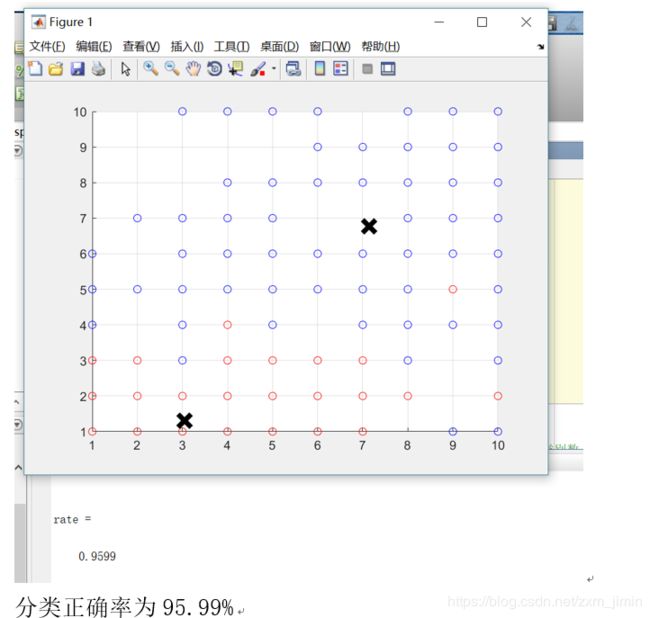
[ctrs idx]=myKmeans(data1,2);
%%
m=size(idx,1);
totalSum = 0 ;%总的正确率
t=data(:,1);
for i = 1 : m
if(idx(i,9)==2)
t(i,1)=4;
else
t(i,1)=2;
end
end
d2 = data(:,11);%提取原始数据中属于第1类的数据的最后一列
%t=[data(:,size(data,2)),idx(:,1)];%把测试数据最后一列,也就是分类属性 和 分类结果取出来:列 + 列
for i = 1 : m
if(t(i,1)==d2(i,1))
totalSum=totalSum+1;
end
end
size(t,1)%总数
totalSum
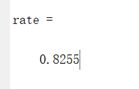
rate = totalSum/size(t,1)%良性的个数
figure;
hold on;
for i=1:m
if idx(i,9)==1
plot3(data1(i,1),data1(i,2),data1(i,3),'ro');
elseif idx(i,9)==2
plot3(data1(i,1),data1(i,2),data1(i,3),'bo');
else
plot3(data1(i,1),data1(i,2),data1(i,3),'ro');
end
end
plot3(ctrs(:,1),ctrs(:,2),ctrs(:,3),'kx','MarkerSize',14,'LineWidth',4);
grid on;%表示在画图的时候添加网格线
数据集2调用略有不同,大体相同,这里省略。
四、实验结果总结
代码2:
myKmeans
kmeans方法正确率
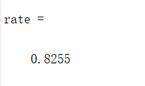
fcm方法正确率

代码2:
myKmeans:

myfcm:
实验结果与分析:
自己实现的k_means可以实现分类,并且分类准确率与kmeans函数相仿。可以看出fuzzy c means方法的分类正确率略优与k-means方法,可能是因为只是分为两类,所有优势不是很明显。
因为其实患者的数据特征有时不能区分得很明显,然而k-means方法对边缘模糊,或者流形的数据的分类效果其实比较不好,因为它每次计算和更新中心点是理由当前属于这一类别的点。
但是fuzzy c means方法对此类问题的分类效果会比K-means方法好一些,应为它每次都是利用所有的点来计算,更新中心点,同时,它的时间代价也会比较大。
但是,两种方法的识别准确率都达到95%以上,如果投入实际原因,相信也会有不错的效果,帮助医生诊断病情,患者了解病情。
实验总结:
通过这次实验,我更加了解了模糊算法的实现方式,k-means方法与fuzzy c means方法的区别,虽然遇到不少小问题,但是这些问题帮助我更好的理解了模糊算法的工作原理,但是自己实现方面只能是做到针对指定数据集进行分类,因为函数中有一部分涉及到输入属性的个数,并且,因为能力不足,还是有稍微借鉴网上的资料,之后将提升自身能力,尽量努力自己实现。如果可以设计出可以放入图像,自动检测的软件,可能会更有现实意义的帮助。
本文为基于前人基础加以改进,若有侵权请私聊我,我注明出处。
转载请注明出处。
代码下载:
https://download.csdn.net/download/zxm_jimin/10976961
https://download.csdn.net/download/zxm_jimin/10976959