视觉惯性SLAM: VI ORB-SLAM

这篇博客

 之前看了VI ORB-SLAM的论文，现在终于有时间来写论文的学习笔记(不容易啊)。因为这是第一次看视觉惯性SLAM论文，所以写这篇博客来详细地记录一下，以后发现问题会再做修改。话不多说，直接进入正题。

视觉惯性SLAM

 只使用相机或惯性元件(IMU)传感器搭建的SLAM系统会存在诸多问题。因为相机虽然可以很好地完成闭环检测和定位，但是它易受到模糊等影响，所以运动速度不能过快。而IMU却可以在速度较快，或周围环境纹理较少时完成定位操作。不过它不能实现闭环检测，且很容易产生漂移现象（因为存在加速度偏差和陀螺仪偏差：即使IMU元件不动，测量值也可能不为0）。
 这么看来这两个传感器的功能刚好能够互补，用相机来帮助IMU消除累积误差，并完成闭环检测；用IMU帮助相机解决在纹理少、运动快的情况下的定位问题。因此，视觉惯性SLAM也就诞生了。
 VI ORB-SLAM是由ORB-SLAM和IMU模块组成，它的大部分环节功能和ORB-SLAM是相似的，所以相似部分之后就不会过多地介绍。

预备知识

符号说明：

 这里提前说一些之后会在公式中使用的符号和变量。
1、惯性传感器（IMU）的坐标系记为：$B$ (Body)
2、相机传感器的坐标系记为：$C$（Camera）
3、世界坐标系记为：$W$
4、IMU中的加速度偏差：$b_a$
5、IMU中的陀螺仪偏差：$b_g$
6、IMU中两次测量值之间的时间间隔：Δt
7、IMU在世界坐标系中的方向：$R_{WB}$（从B坐标系到W坐标系的旋转矩阵）
8、将B坐标系的速度在W坐标系中表示：${}_W{V}_B$
9、将B坐标系的位置在W坐标系中表示：${}_W{P}_B$（B到W坐标系之间的平移变换）
10、重力加速度：$g_W$
11、重力方向：$\widehat{g_W}=\frac{g_W^{\ast }}{\Vert g_W^{\ast }\Vert }$
12、重力的大小$G$
13、IMU测得的加速度大小：$a_B$
14、IMU测得的角速度大小：$w_B$
15、B坐标系到相机坐标系的变换矩阵：$T_{CB}=[R_{CB}{|}_C{P}_B]$

相机投影变换矩阵

 基于小孔成像模型来算出相机坐标系与像素坐标系之间的变换矩阵，并定义投影函数$\pi$:
  $\pi (X_C)=\left[\begin{array}{c}{f}_u\frac{X_C}{Z_C}+c_u\\ f_v\frac{Y_C}{Z_C}+c_v\end{array}\right],X_C=[X_C{Y}_C{Z}_C{]}^T.............(1)$
式中 $[f_u,f_v{]}^T$表示焦距长度，$[c_u,c_v]$表示主点位置。它们的单位都为像素。

IMU数据更新方程

 更新的量有三个：$R，p，v$。更新的公式如下：

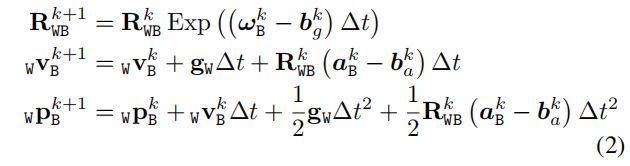 这个公式是从参考文献[1]中获得的，表示的是前后两帧之间的变量关系（和参考文献[1]不同的是，这里忽略了噪声对角速度、加速度测量值的影响）。这是之后实现IMU数据预积分的基础。

IMU数据的预积分

 预积分就是计算出两相邻帧或关键帧之间的IMU数据的总变化量$（\Delta R，\Delta p，\Delta v）$，它由相邻帧或关键帧之间所有的IMU测量数据叠加后获得。在VI ORB-SLAM中用这个公式表示预积分：

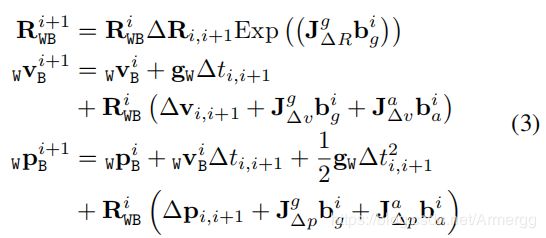
 这个公式也是从参考文献[1]中获得的。其中$J_{\Delta v}^g{b}_g^i$表示第 i 帧的陀螺仪偏差对于$\Delta v$的影响量，$J_{\Delta v}^g$是$\Delta v$关于$b_g$的雅可比矩阵。其他与此类似的变量也是这个意思。

VI ORB-SLAM各环节工作方式

 因为是基于ORB-SLAM搭建的系统，所以VI ORB-SLAM的工作原理和ORB-SLAM十分相似，也是使用三个线程：Tracking、Local Mapping、Loop Close。不过它们各线程的具体工作内容有所不同，下面来介绍这些不同之处。

Initialization

 在ORB-SLAM中，初始化的任务有：创建出初始地图、定义第一参考帧和轨迹的尺度。在VI ORB-SLAM中，除了上述任务外，初始化还要估计出IMU设备的重力方向、加速度和陀螺仪偏差等变量。它的步骤是：
1、先使用最原始的视觉初始化，获得初始地图和一定数量的关键帧；
2、进行IMU传感器的初始化，初始化其重力方向、加速度和陀螺仪偏差、速度，以及整个轨迹对应的尺度。
 这个部分的内容放在最后再说。

Tracking

 跟踪线程负责计算状态变量：$(R,p,v,b)$，即机器位姿、速度和IMU传感器的偏差。计算速率和相机的帧率相同（因为IMU数据的采集速率快，不能给每个数据找到其对应的图像数据。图像数据则刚好相反）。
 在估计出状态变量后，对估计值进行优化。所以整个线程的工作流程如下：
1、估计出当前帧的状态变量；
2、将地图中的地图点投影到当前帧上，寻找匹配特征点；
3、计算这些匹配点的重投影误差以及相应帧之间的IMU误差；
4、求得总误差，通过最小化总误差来完成状态变量的优化。

图1

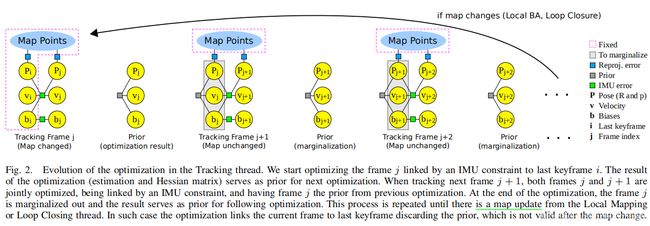
 这里需要注意的是：根据地图是否更新(有无新的关键帧产生或检测到闭环)，上述流程中第3、4步会有两种不同的计算方法
(a)当地图发生了更新：只有优化当前帧的状态
 使用更新后的地图和最后一个关键帧作为优化的参考，它们在优化过程中保持不变。如下图所示：

图2

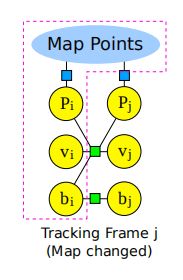
图中来自最后一个关键帧的变量用下标 $i$ 表示，来自当前帧的则用下标 $j$ 表示。重投影误差用蓝色矩形表示，IMU误差则是绿色矩形。红色框表示固定的变量。
 在当前情况下，待优化的状态变量和优化方式为：

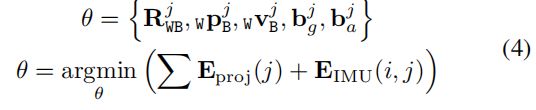
式中$E_{proj}$表示地图点与当前帧产生的重投影误差，$E_{IMU}$表示关键帧与当前帧产生的IMU误差。$E_{proj}$的计算公式:

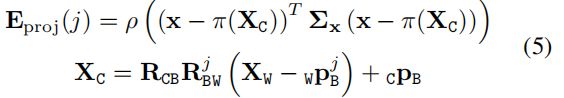
式中$X_C$是地图点在相机坐标系下的坐标(计算原理可理解为：${}_W{p}_B$是IMU在世界坐标系下的坐标，用$X_W$（地图点的世界坐标）减去${}_W{p}_B$就能获得该地图点与${}_W{p}_B$之间的向量(世界坐标系)。然后对该向量进行旋转平移变换，就能获得地图点在B坐标系下的坐标)。
 IMU误差的计算公式为：

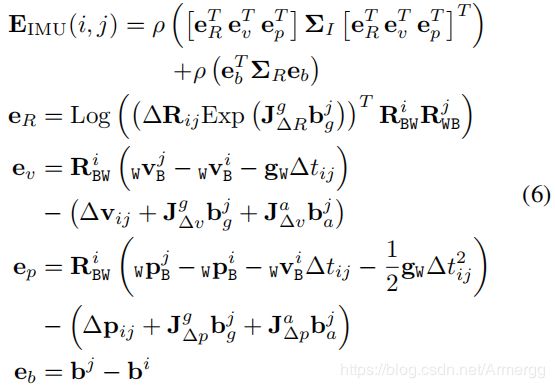
 式6是在文献[1]中获得的。
个人理解：感觉$e_v,e_p$的计算和文献[1]中不符，使用的$b_{(.)}^j$应该是$b_{(.)}^i$。
 之后使用非线性优化的方式优化误差。最后将当前帧的优化结果和Hessian矩阵设为一个先验信息，给后续帧做参考。

(b) 地图未更新：同时优化前后两帧，但保持地图点不变

图3

 从图中可看出，这个情况下只用地图点保持不变，且优化的对象从一个当前帧增加到前后两帧，对应的待优化状态变量也变成了：

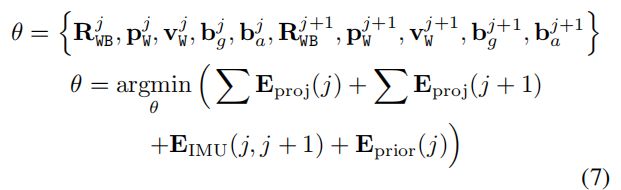
式中$E_{prior}$是前一帧保留的先验信息产生的先验误差（图3中的小灰色正方形），它的计算公式为：

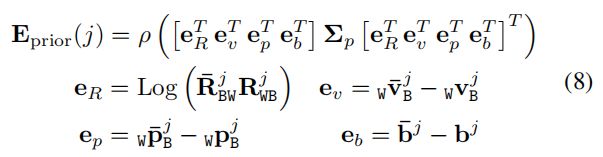
式中带横线的变量表示前一帧的先验信息，不带横线的表示前一帧在当前优化中的结果。$\rho$是一类鲁棒核函数。
个人理解：$E_{prior}$：在当前优化过程中可以调节前一帧的状态变量，但不能使其变化太多(好像可以防止累积误差)
 在完成优化后，上一帧就被边缘化（抛弃），而当前帧的优化结果又将作为新的先验信息。这个方法一直持续到地图发生更新或先验信息无效为止。

LocalMapping

 VIORB-SLAM和ORB-SLAM的局部建图环节不同的地方在于：前者在进行LocalBA时要多考虑一个IMU的误差项约束。这两个系统在LocalBA上的对比图如下：

图4

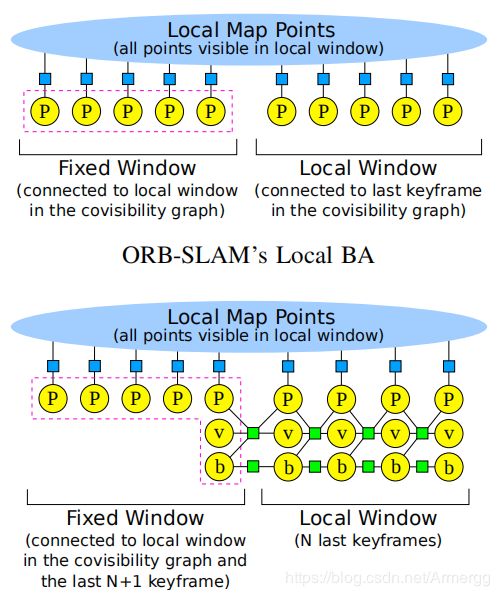
相同点：只保留和优化N个关键帧，以及它们观测到的所有地图点。不过其余能够观测到这些地图点的关键帧也会在LocalBA中被使用。它们给地图点提供重投影误差的约束，自身的状态是不变的（在红色框内的部分）。
不同点：VIORB-SLAM要考虑各关键帧之间的IMU约束，以及第N+1个关键帧（红框最右边）对其下一关键帧的IMU约束。

Loop Closing

 VIORB-SLAM 和 ORB-SLAM在闭环检测环节上是差不多的。当检测到闭环之后，会对闭环中的关键帧进行位姿图优化（减少计算量），只优化位姿$（R,p）$，而不优化IMU变量$（v，b）$。
 值得注意的是，位姿图中优化的状态变量只有6个自由度，因为尺度信息可以在IMU初始化时估计出来。这和ORB-SLAM是不同的。
个人理解：因为闭环匹配上的两个关键帧之间很难有IMU的数据约束，所以位姿优化不优化IMU变量

Full BA

 使用一个独立的线程进行Full BA，优化所有状态量：位姿，速度和偏差。

IMU初始化

 这是整个VI ORB-SLAM的核心部分，用于估计重力方向、尺度($s$)、速度($v$)、IMU的偏差($b_a,b_g$)。整个过程为：
1、估计陀螺仪偏差($b_g$)
2、粗略估计尺度($s$)和重力向量($g_W$)（不考虑加速度偏差的影响）
3、估计加速度偏差($b_a$)，并优化尺度($s$)和重力方向
4、估计速度($v$)
需要注意的是任两个相邻的关键帧的时间间隔要短，以减少测量噪声的影响。下面介绍各步骤的具体内容。

估计$b_g$

 可以通过每两个相邻关键帧之间的旋转测量值来估计陀螺仪偏差：

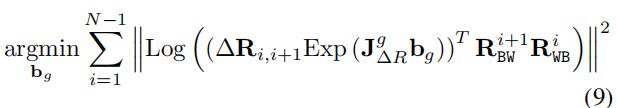式中$R_{(.)}$表示由视觉求出的关键帧间的旋转变换，$\Delta R_{i,i+1}$表示通过预积分求出的关键帧间变换关系。

 优化过程中假设$b_g$保持不变，通过最小化上述误差项来估计出$b_g$。

估计尺度$s$和重力向量$g_W$（不考虑加速度偏差$b_a$）

 在求出$b_g$之后，可以预积分出速度($v$)和位置($p$)。
 由于单目SLAM估计的轨迹存在一个尺度因子$s$，所以在轨迹中描述IMU元件与相机之间的变换关系时要考虑$s$，即构建如下变换公式：

 将式(10)带入到式(3)，同时忽视其中的$b_a$后可得公式：

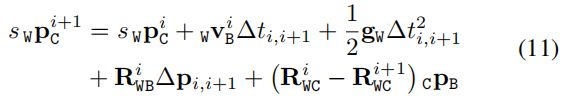
 该式子用于求解 $s$ 和 $g_W$ ，由求解线性方程来实现。为了避免求解速度变量，降低方程复杂度，使用三个连续关键帧之间存在的两个相对位姿关系，以及式子(3)中的速度计算公式，来构建线性方程组：

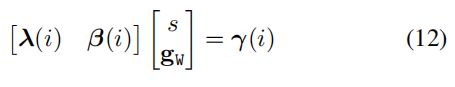
 为了方便，将关键帧 $i、i+1、i+2$写作$1、2、3$。方程组中各项的表达式为：

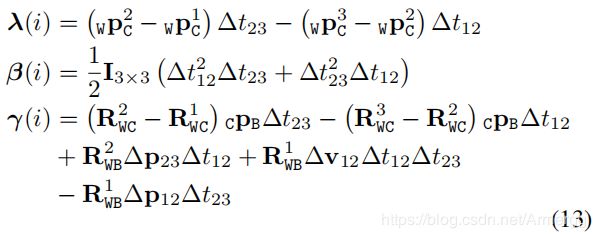
 方程组(12)的形式为$A_{3(N-2)X4}{x}_{4X1}=B_{3(N-2)X1}$。使用SVD求解方程组(12)，获得$s^{\ast },g_W^{\ast }$。由于未知量的自由度为 4，所以至少需要有4个关键帧才能求解方程组。

估计加速度偏差($b_a$)，尺度($s$)和重力方向

 前面获得的$s^{\ast },g_W^{\ast }$未考虑加速度偏差($b_a$)，原因是加速度偏差和重力很难区分开==(重力会影响到$b_a$，两者相关性较大)==。而重力的方向和加速度偏差区分性很好，所以可以同时估计这两者的量。
 首先认为在一个参考的惯性坐标系I中，重力的方向为$\widehat{g_I}=\{0,0,-1\}$，大小为$G$。而之前计算出来的$g_W^{\ast }$的方向为$\widehat{g_W}=\frac{g_W^{\ast }}{\Vert g_W^{\ast }\Vert }$。这时计算$W、I$坐标系之间的旋转变换：

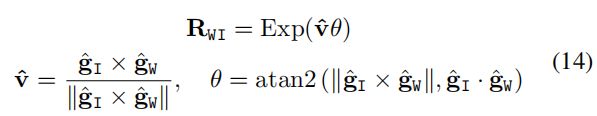
个人理解：之前求出的$g_W^{\ast }$是在第一参考帧(所有轨迹的世界坐标系)中的，而$g_I$是真实世界中重力的方向。求出$R_{WI}$后就能够获得所有轨迹与真实世界之间的旋转关系(修正位姿估计值的方向)
 此时$g_W$可以表示成：$g_W=R_{WI}\widehat{g_I}G$ …(15)

式中的$R_{WI}$只包含x、y两个轴上的旋转角度，因为z轴的旋转不会影响到重力的方向。
 通过下面这个扰动来优化旋转$R_{WI}$：

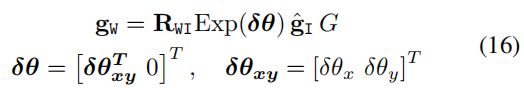
 式(16)的一阶近似为：

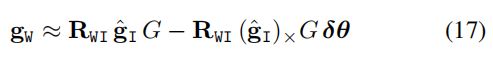(PS：关于扰动和一阶近似可以参考《视觉SLAM十四讲》P75、P110)

 将式(17)带入到式(11)中，并考虑$b_a$的影响，可得：

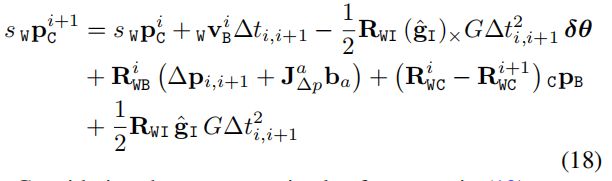
 仍是使用三个关键帧，得到如下线性方程组：

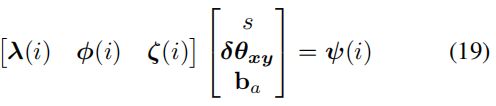其中各项的表达式为($\lambda (i)$和方程组(12)中的一样)：

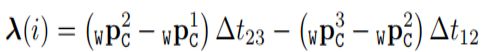
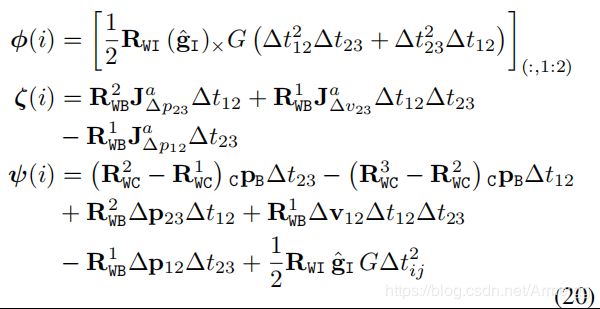
式中$[{]}_{(:,1:2)}$表示矩阵的前两列
 方程组(19)的形式为$A_{3(N-2)X6}{x}_{6X1}=B_{3(N-2)X1}$。通过SVD的方法求解(19)，求出$s^{\ast },\delta {\theta }_{xy}^{\ast },b_a^{\ast }$，以及条件数。由于待求变量的自由度为6，所以至少需要4个关键帧。
PS：条件数可用于检查此问题是否条件良好(如：IMU执行的运动使所有变量均可观察)[2]

速度($v$)估计

 可以通过式(18)求出（用来初始化使用的）关键帧的速度，因为此时$s、g_W、b_a、b_g$都已知。此外，还可以使用公式(3)求出最近的关键帧的速度。

在重定位后重新初始化$b_g,b_a$

 如果系统在长期运行后进行了重定位操作，则使用式(9)重新初始化$b_g$。而$b_a$则通过式(19)求出，此时$s、g_W$都是已知的。此过程使用20个连续的帧来完成，这些帧都是由视觉估计位姿。

结尾

 这篇博客是自己对视觉惯性SLAM领域的一个初步探索，里面也加入了一些自己的理解。虽然VI ORB-SLAM的作者没有开源代码，但是网上有前辈根据论文复现了系统(感谢前辈！！)。所以又有事情可做了/(-o-)/~~。

参考资料：
1、https://arxiv.org/pdf/1610.05949.pdf
2、https://blog.csdn.net/myarrow/article/details/54694472(这篇博客写的真不错！！)