字符串系列4 后缀数组
阅读目录:
文章目录
- 简介
- 倍增法
- DC3
- 最长前缀
- 附录
- 倍增法 C++ 实现( [hiho 1403](https://hihocoder.com/problemset/problem/1403) )通过
- DC3算法 C++ 实现( [hiho 1403](https://hihocoder.com/problemset/problem/1403) )通过
简介
后缀数组就是把一个文本串的所有后缀按字典序从小到大排放的数组。由于线性构造后缀树比较复杂,因此后缀数组和后缀自动机都是替代方案,也能完成大部分功能。那么这三个算法和之前介绍那么多算法有什么区别呢,之前介绍的算法可以说都是处理模式串的,而后缀数组和后缀自动机都是处理文本串的。
之前算法需要事先知道的模式串,然后对于一个在线输入的文本串进行匹配,也就是说模式串一定要事先知道,需要匹配的文本可以动态的输入。
而后缀数组需要事先知道整个文本串,模式串可以一个一个的动态输入。在实际应用中,你很多时候是无法事先知道要查询的模式串的(如搜索引擎)。假设你要查找一篇(或多篇)文章里面有没有出现一个词组(模式串),你可以先预处理该文本,利用后缀数组和你输入的这个词组(模式串),就可以在 O ( m + l o g n ) O(m+logn) O(m+logn) 时间复杂度的算法)的时间复杂度你可以知道该词组(模式串)出现的所有位置(如果此时用KMP去找匹配点的话,复杂度为 O ( n + m ) O(n+m) O(n+m),在文本串长度n远大于模板串长度m时代价太高)。
比如说字符串 aabaaaab$,我们暂且把$认为是一个字符(表示字符串结尾,程序中用0代替)。我们记 suffix(i) 表示从原字符串第 i 个字符( 0 ⩽ i ⩽ n − 1 0\leqslant i \leqslant n-1 0⩽i⩽n−1)开始到字符串结尾的后缀。我们把它所有的后缀拿出来按字典序排序:
| 后缀 | i |
|---|---|
| $ | 8 |
| aaaab$ | 3 |
| aaab$ | 4 |
| aab$ | 5 |
| aabaaaab$ | 0 |
| ab$ | 6 |
| abaaaab$ | 1 |
| b$ | 7 |
| baaaab$ | 2 |
并且我们把排好序的下标数组记做 sa,比如 sa[1]=8,sa[4]=5(这里假设最小的排名为1,0也无所谓)。我们用数组 rank 表示字符串 S 的名次数组,表示将 S 的 n 个后缀从小到大排序后,后缀 suffix[i] 的排名是 rank[i],比如上个字符串中 rank[8]=1,rank[5]=4。很明显,sa[rank[i]]=i。
给出一个字符串 S,长度为 n,当然根据定义也能暴力地求解后缀数组,但是我们需要更快的方法,有两种方法计算这个 sa,倍增法和 DC3 法,倍增法的时间复杂度是 O ( n l o g ( n ) ) O(nlog(n)) O(nlog(n)),DC3的时间复杂度是 O ( n ) O(n) O(n)。两个方法的空间复杂度都是 O ( n ) O(n) O(n)。
倍增法
- 首先对于每一个后缀的第1个字符排序,即计算 S[0], S[1], …, S[n-1] 的排名,比如对于 aabaaaab,排序后为:1,1,2,1,1,1,1,2。
- 接下来,我们再对所有后缀的前两个字符排序,将步骤1的相邻二元组合并,若后缀不足两个字符,拿 $ 符号补位,由于单个字符的顺序已经计算完毕,所以合并之后的所有的两位数的每个数位的顺序都已经计算完毕,因此这里采用基数排序重新计算合并之后的两位数的顺序。
- 然后我们再对所有后缀的前4个字符的排序,即计算S[0,1,2,3], S[1,2,3,4], S[2,3,4,5], …, S[n-4,n-3,n-2,n-1], S[n-3,n-2,n-1,$], S[n-2,n-1,$,$], S[n-2,$,$,$] 的排名,由于后缀 x 的前4个字符是由后缀 x 的前2个字符和后缀 x+2 的前2个字符组成的,并且这两个信息我们已经计算出来,因此再次基数排序即可。
- 依次类推,每次使用两个 2 x − 1 2^{x-1} 2x−1 长度的子串来计算 2 x 2^x 2x 长度的子串的排名,直到某一次排序后 n 个数字各不相同。
这里采用 Python 实现( hiho 1403 通过 ),其中 cal_height 函数是计算最长前缀使用的,下面有介绍,建议看完这部分再总体看代码,或者只看 da 函数就行,该有的注释我都写了,如果看不明白就结合注释以及断点自己悟吧,附录中有 C++ 模板:
# -*- coding: UTF-8 -*-
# da 算法
N = 20001 # 字符串最大长度
wa, wb, wd = ([0 for _ in range(N)] for i in range(3)) # 基数排序辅助数组
ra, s = ([0 for _ in range(N)] for i in range(2)) # rank 数组和字符串数组
def cmp_len(s, a, b, l):
return s[a] == s[b] and s[a + l] == s[b + l]
def da(s, sa, n, m):
s[n] = 0
n += 1
x, y = wa, wb
# 基数排序计算长度为1的子串的排名,相同的越靠前排名越小
for i in range(m): wd[i] = 0
for i in range(n): x[i] = s[i]; wd[x[i]] += 1
for i in range(1, m): wd[i] += wd[i - 1]
for i in range(n - 1, -1, -1): wd[x[i]] -= 1; sa[wd[x[i]]] = i
j = p = 1
while p < n:
p = 0
# y[p] 存储着第2关键字排名为 p 的下标,即 y[p]==i 表示第2关键字为第 p 名的是后缀 i
# 由于当前处理的是每个后缀的前缀的[j,2*j-1]字符
# 而后缀 n-j 到后缀 n-1 不存在第j个字符,所以他们的第2关键字的名字自然优先
for i in range(n - j, n, 1): y[p] = i; p += 1
# 除了上面那些后缀不存在第2关键字
# x+j 后缀的第1关键字排名 - j 等于 x 后缀的第2关键字排名
for i in range(0, n):
if sa[i] >= j: y[p] = sa[i] - j; p += 1
# 这里倒着枚举,当两个位置的 y[i] 和 y[j](假设i
# 即 y 的排名大 而 x 在外面也决定了排名以第一关键字为主
for i in range(m): wd[i] = 0
for i in range(n): wd[x[i]] += 1
for i in range(1, m): wd[i] += wd[i - 1]
for i in range(n - 1, -1, -1): wd[x[y[i]]] -= 1; sa[wd[x[y[i]]]] = y[i]
x, y = y, x
# 根据当前 sa 数组重新计算 x,即下轮排序的第一关键字的排名
x[sa[0]], p = 0, 1
for i in range(1, n):
if cmp_len(y, sa[i - 1], sa[i], j): x[sa[i]] = p - 1
else: x[sa[i]] = p; p += 1
j, m = j << 1, p
def cal_height(s, sa, n, height):
j = k = 0
for i in range(0, n + 1): ra[sa[i]] = i
for i in range(0, n):
if k != 0: k -= 1
j = sa[ra[i] - 1]
while i + k < n and j + k < n and s[i + k] == s[j + k]: k += 1
height[ra[i]] = k
# oj 需要
while True:
try:
b = raw_input().split(" ")
n, k = int(b[0]), int(b[1])
for i in range(n):
s[i] = input()
sa, height = ([0 for _ in range(n + 1)] for i in range(2))
da(s, sa, n, 127)
cal_height(s, sa, n, height)
if k == 0:
print str(n) + '\n'
continue
ans = 0
for i in range(1, n - k + 2):
mm = 0x3f3f3f3f
for j in range(0, k - 1):
if mm > height[i + j]:
mm = height[i + j]
if mm > ans: ans = mm
print ans
except EOFError:
break
DC3
这个算法叫 DC3,这个3有很多实际意义,我们边分析边看。
首先,算法的核心思想就是先计算是模3不等于0的所有位置开始的后缀的排名,再计算模3等于0的所有位置的后缀的排名,然后将它们合并起来,得出所有位置的后缀的排名。因此下面的讲解也分三部分进行。这里还是拿 S=aabaaaab 来说明。
-
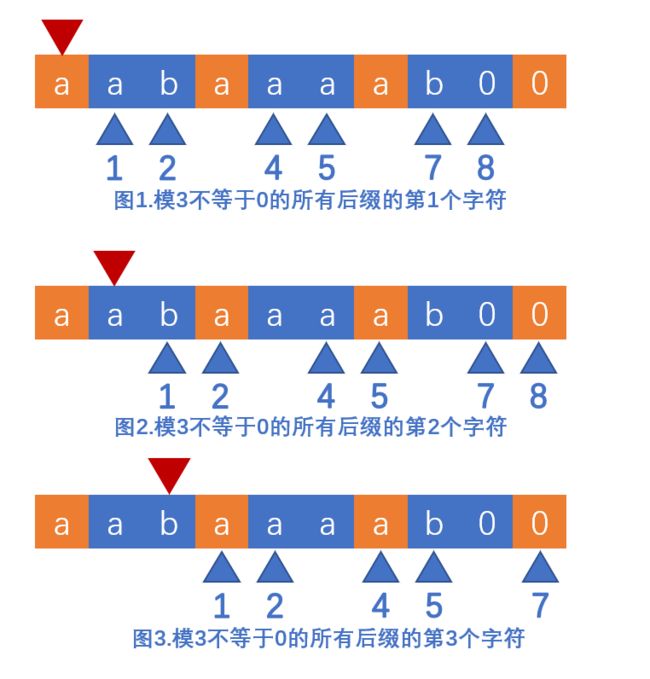
首先计算模3不等于0的所有位置开始的后缀的排名,比如这里来说就是计算 Suffix[1], Suffix[2], Suffix[4], Suffix[5], Suffix[7], Suffix[8],在下图中就是蓝色方块的位置开始的后缀。我们先只对这些后缀的前三个字符进行排序,对于 aabaaaab 来说求出 aba, baa, aaa, aab, ba0, a00 这六个的排名为 3,5,1,2,4,0(注意,如果排序后还有相同的数字,也就是还有两个相同的串,比如 2,1,3,4,1,0,那么要继续求,因为两个2之后的数字4大于1,所以第二的位置的2代表的后缀大于第5个位置的2代表的后缀。其实这个问题跟刚才的问题是相同的,所以可以递归求)。
那么如何高效求出这几个位置的排名呢?由于基数排序首先排序低位,因此我们先观察这些后缀的第3个字符,也就是图3所有蓝色三角指向的位置。你会发现,这些位置恰好是以字符S[2]开始的字符数组的模3不等于0的位置,这在有指针的语言中可以直接以S[2]地址为首地址,直接对之前算出的模3不等于0的位置的所有字符进行排序来实现,而在非指针的语言中可以采用对模3不等于0的位置加1进行排序。而后缀的第2个字符恰好是以字符S[1]开始的模3不等于0的位置,排序方法和第三个字符是一样的。后缀的第1个字符恰好是以字符S[0]开始的模3不等于0的位,这个数位的排序方法和前两个是一样的。
当有两个后缀的前三个字符排名相同时,我们又如何继续进行递归呢?我们需要转换坐标才能继续递归,如下图所示,我们已经求出所有模3不等于0的后缀的前3个字符,我们不妨将每三个字符看做一个整体,然后重新赋予如下图所示下标。其中以新字符串3, 4, 5下标对应的字符开始的字符串就是原字符串的模3等于2的位置的后缀,而新字符串0, 1, 2下标对应的字符开始的字符串就是原字符串的模3等于1的位置的后缀再加上一些字符,新字符串这六个位置的排名就是原字符串模3不等于0位置的排名。下面简单说明一下加上那些字符为啥不会影响排名,首先新字符串中由于0, 1, 2都加了相同的字符串,因此肯定不会影响他们三个之间的排名,再拿0和3举例子说明也不会影响0, 1, 2和3, 4, 5之间的排名,如果S[0:] > S[3:],那么肯定在某个位置x存在字符S[0:][x] > S[3:][x],而S[0:]末尾是0,比任何非0字符都小,因此这个位置肯定在末尾之前,因此后面加的那些字符串都不重要了,如果S[0:] < S[3:],那么肯定在某个位置x存在字符S[0:][x] < S[3:][x],而S[3:]末尾是0,比任何非0字符都小,因此这个位置肯定在末尾之前,因此后面加的那些字符串都不重要了。

-
计算模3等于0的位置的排名。这些位置的后缀,可以看做一个字符加上某个第一部分的一个后缀,这也很容易通过一次基数排序(就像倍增法的二元组一样)求得。对于上面的串,模3为0的后缀的排名为 Suffix[9] < Suffix[3] < Suffix[0] < Suffix[6]。

-
合并第一部分和第二部分的排名。注意,上面求出的第一部分第二部分的排名都没有考虑另外一部分。合并的时候我们需要比较第一部分的某个后缀和第二部分的某个后缀。分两种情况。第一种是比较 Suffix[3*i] 和 Suffix[3*j+1],我们把它们看做:
Suffix[3*i] = S[3*i] + Suffix[3*i+1]
Suffix[3*j+1] = S[3*j+1] + Suffix[3*j+2]
Suffix[3*i+1]和Suffix[3*j+2]可以直接比较,因为它们都属于第一部分,而S[3*i]和S[3*j+1]也可以直接比较;
第二种情况是 Suffix[3*i] 和 Suffix[3*j+2],把它们看做是
Suffix[3*i] = S[3*i] + S[3*i+1] + Suffix[3*i+2]
Suffix[3*j+2] = S[3*j+2] + S[3*j+3] + Suffix[3*(j+1)+1]
Suffix[3*i+2] 和 Suffix[3*(j+1)+1] 可以直接比较,它们都属于第二部分。而前面是两个单个字符,可以直接比较。这样,就可以合并所有的后缀得到答案。
Python 代码如下( hiho 1403 通过 ),其中 cal_height 函数是计算最长前缀使用的,下面有介绍,建议看完这部分再总体看代码,或者只看 dc3 函数就行,该有的注释我都写了,如果看不明白就结合注释以及断点自己悟吧,附录中有 C++ 模板:
# -*- coding: UTF-8 -*-
# dc3 算法
N = 20003 # 字符串最大长度
wa, wb, wd, wv = ([0 for _ in range(N)] for i in range(4)) # 基数排序辅助数组
ra, s = ([0 for _ in range(N)] for i in range(2)) # rank 数组和字符串数组
def c0(r, a, b):
return r[a] == r[b] and r[a + 1] == r[b + 1] and r[a + 2] == r[b + 2]
def c12(k, r, a, b):
if k == 2:
return r[a] < r[b] or r[a] == r[b] and c12(1, r, a + 1, b + 1)
else:
return r[a] < r[b] or r[a] == r[b] and wv[a + 1] < wv[b + 1]
def sort(s, a, b, n, m):
if not s: return
for i in range(n): wv[i] = s[a[i]]
for i in range(m): wd[i] = 0
for i in range(n): wd[wv[i]] += 1
for i in range(1, m): wd[i] += wd[i - 1]
for i in range(n - 1, -1, -1): wd[wv[i]] -= 1; b[wd[wv[i]]] = a[i]
def dc3(s, sa, n, m):
ta, tb, tbc = 0, (n + 1) / 3, 0
for i in range(n):
if i % 3 != 0: wa[tbc] = i; tbc += 1
sn, san = ([0 for _ in range(tbc + 3)] for _ in range(2)) # 辅助数组
sort(s[2:], wa, wb, tbc, m) # 排序模3不等于0位置的最后1个字符
sort(s[1:], wb, wa, tbc, m) # 排序模3不等于0位置的最后2个字符
sort(s, wa, wb, tbc, m) # 排序模3不等于0位置的最后3个字符
def F(x): return x / 3 + [tb, 0][x % 3 == 1]
def G(x): return [(x - tb) * 3 + 2, x * 3 + 1][x < tb]
sn[F(wb[0])] = 0
p = 1
for i in range(1, tbc):
if c0(s, wb[i - 1], wb[i]): sn[F(wb[i])] = p - 1
else: sn[F(wb[i])] = p; p += 1
if p < tbc: dc3(sn, san, tbc, p)
else:
for i in range(tbc): san[sn[i]] = i
# 第一部分计算完毕
for i in range(tbc):
if san[i] < tb: wb[ta] = san[i] * 3; ta += 1
if n % 3 == 1: wb[ta] = n - 1; ta += 1
sort(s, wb, wa, ta, m)
# 第二部分计算完毕
# 此时 wv 相当与第一部分的一个 rank,即以 G(san[i]) 开始的的后缀排名为 i
for i in range(tbc): wb[i] = G(san[i]); wv[wb[i]] = i
p = i = j = 0
while i < ta and j < tbc:
if c12(wb[j] % 3, s, wa[i], wb[j]): sa[p] = wa[i]; i += 1
else: sa[p] = wb[j]; j += 1
p += 1
while i < ta: sa[p] = wa[i]; i += 1; p += 1
while j < tbc: sa[p] = wb[j]; j += 1; p += 1
def cal_height(s, sa, n, height):
j = k = 0
for i in range(1, n + 1): ra[sa[i]] = i
for i in range(0, n):
if k != 0: k -= 1
j = sa[ra[i] - 1]
while i + k < n and j + k < n and s[i + k] == s[j + k]: k += 1
height[ra[i]] = k
# 这部分是 oj 题的需要
while True:
try:
b = raw_input().split(" ")
n, k = int(b[0]), int(b[1])
for i in range(n):
s[i] = input()
sa, height = ([0 for _ in range(n + 3)] for i in range(2))
dc3(s, sa, n + 1, 101)
cal_height(s, sa, n, height)
if k == 0:
print str(n) + '\n'
continue
ans = 0
for i in range(1, n - k + 2):
mm = 0x3f3f3f3f
for j in range(0, k - 1):
if mm > height[i + j]:
mm = height[i + j]
if mm > ans: ans = mm
print ans
except EOFError:
break
最长前缀
在求出 sa 数组之后,我们定义一个新的数组 height,height[i] 表示 Suffix[sa[i-1]]与 Suffix[sa[i]] 的最长公共前缀,也就是排名为 i 和排名为 i-1 的两个后缀的最长公共前缀。如果我们求出了 height 数组,那么对于任意两个位置 i,j,我们不妨设 rank[i] 小于 rank[j],它们的最长公共前缀就是 height[rank[i]+1], height[rank[i]+2], …, height[rank[j]] 的最小值。比如字符串为 aabaaaab,我们求后缀 Suffix[1]=abaaaab 和 Suffix[4]=aaab 的最长公共前缀,如下图所示:

那么如何计算 height?我们定义 h[i]=height[rank[i]],也就是 Suffix[i] 和它前一名的最长公共前缀,那么很明显有 h[i]>=h[i-1]-1,因为 h[i-1] 是 Suffix[i-1] 和它前一名的最长公共前缀,设为 Suffix[k],那么 Suffix[i] 和 Suffix[k+1] 的最长公共前缀为 h[i-1]-1,所以 h[i] 至少是 h[i-1]-1。所以我们可以按照求 h[1], h[2], h[3] 顺序计算所有的height。
附录
倍增法 C++ 实现( hiho 1403 )通过
#include DC3算法 C++ 实现( hiho 1403 )通过
#include
int *sn = s + n + 2, *san = sa + n + 2, ta = 0, tb = (n + 1) / 3, tbc = 0, p;
// s[n - 1] = s[n + 1] = s[n] = 0 // 若令 s[n - 1] = 0,在递归时会将 sn[tbc - 1] 置 0
// s[n + 1] = s[n] = 0; // 方便排序操作
for (int i = 0; i < n; i++) if (i % 3 != 0) wa[tbc++] = i;
sort(s + 2, wa, wb, tbc, m);
sort(s + 1, wb, wa, tbc, m);
sort(s, wa, wb, tbc, m);
sn[F(wb[0])] = 0;
p = 1;
// 这个很好理解,就是想判断是否有完全相同的关键字,相同,则rn数组内存的值相等
for (int i = 1; i < tbc; i++)
sn[F(wb[i])] = c0(s, wb[i - 1], wb[i]) ? p - 1 : p++;
// 如果p
if (p < tbc) dc3(sn, san, tbc, p);
else for (int i = 0; i < tbc; i++) san[sn[i]] = i;
// 第一部分计算完毕
// 先令san[i]==j;如果j
for (int i = 0; i < tbc; i++) if (san[i] < tb) wb[ta++] = san[i] * 3;
// 因为san中没有suffix(n),所以要特殊处理
if (n % 3 == 1) wb[ta++] = n - 1;
// wb中存储按照第二关键字有序的第一关键字的下标。排好第一关键字后,wa中存放
// 按照两个关键字有序的的第一关键字的下标,即%3==0的下标开始后缀数组的排序结果。
sort(s, wb, wa, ta, m);
// 第二部分计算完毕
// 开始合并
// 此时wv相当与第一部分的一个rank,即以G(san[i])开始的的后缀排名为i
for (int i = 0; i < tbc; i++) wv[wb[i] = G(san[i])] = i;
int i = 0, j = 0;
for (p = 0; i < ta && j < tbc; p++)
sa[p] = c12(wb[j] % 3, s, wa[i], wb[j]) ? wa[i++] : wb[j++];
while (i < ta) sa[p++] = wa[i++];
while (j < tbc) sa[p++] = wb[j++];
#undef F(x)
#undef G(x)
}
public:
// 字符串S, 长度n, S[0,n-1],为方便,我们假设它只包含小写字母
// 最后的后缀数组存储在SA[1~n]中 1<=SA[i]<=n
void calSuffixArray(char *S, int n, int *SA) {
for (int i = 0; i < n; i++) r[i] = S[i] - 'a' + 1;
dc3(r, sa, n + 1, 27); // 假设末尾有一个 0
for (int i = 1; i <= n; i++) SA[i] = sa[i];
}
// 字符串S, 长度n, S[0,n-1],为方便,我们假设它只包含数字
// 最后的后缀数组存储在SA[1~n]中 1<=SA[i]<=n
void calSuffixArray(int *S, int n, int *SA) {
for (int i = 0; i < n; i++) r[i] = S[i];
dc3(r, sa, n + 1, 101); // 假设末尾有一个 0
for (int i = 1; i <= n; i++) SA[i] = sa[i];
}
void calHeight(int *sa, int n, int *height) {
int i, j, k = 0;
for (int i = 1; i <= n; i++) ra[sa[i]] = i;
for (int i = 0; i < n; i++) {
if (k) k--;
j = sa[ra[i] - 1];
while (i + k < n && j + k < n && r[i + k] == r[j + k]) k++;
height[ra[i]] = k;
}
}
};
const int N = 20003;
int a[N];
int main() {
int n, K;
while (cin >> n >> K) {
for (int i = 0; i < n; i++)
scanf("%d", &a[i]);
int sa[n + 3];
int height[n];
SuffixArray *suffixArray = new SuffixArray();
suffixArray->calSuffixArray(a, n, sa);
suffixArray->calHeight(sa, n, height);
if (K == 0) {
printf("%d\n", n);
continue;
}
int ans = 0;
for (int i = 1; i <= n - K + 1; i++) {
#define inf 0x3f3f3f3f
int mm = inf;
for (int j = 0; j < K - 1; j++) {
if (mm > height[i + j])
mm = height[i + j];
}
if (mm > ans)
ans = mm;
}
printf("%d\n", ans);
}
}
参考博客:
- [知识点]后缀数组
- 后缀数组:倍增法和DC3的简单理解
- 后缀数组
