Newton牛顿法(二)| 收敛性和收敛速度 +初值的选取方法
- 收敛性和收敛速度
对Newton法的迭代函数即公式(1)取导数,有:
φ ′ ( x ) = f ( x ) f ′ ′ ( x ) [ f ′ ( x ) ] 2 \varphi'(x)=\frac{f(x)f''(x)}{[f'(x)]^2} φ′(x)=[f′(x)]2f(x)f′′(x)
假定 x ∗ x^* x∗是 f ( x ) = 0 f(x)=0 f(x)=0的一个单根,即 f ( x ∗ ) = 0 , f ′ ( x ∗ ) ≠ 0 f(x^*)=0,f'(x^*)\neq 0 f(x∗)=0,f′(x∗)=0,则有 φ ′ ( x ∗ ) = 0 \varphi'(x^*)=0 φ′(x∗)=0。所以,当x充分靠近 x ∗ x^* x∗时,可使 ∣ φ ′ ( x ) ∣ ≤ L < 1 |\varphi'(x)|\leq L<1 ∣φ′(x)∣≤L<1成立,从而根据迭代法的局部收敛性定理可知,Newton迭代法在单根 x ∗ x^* x∗的邻近是收敛的。即有下面的Newton法局部收敛性定理。
定理1:若 x ∗ x^* x∗为方程 f ( x ) = 0 f(x)=0 f(x)=0的一个单根,即 f ( x ∗ ) = 0 f(x^*)=0 f(x∗)=0和 f ′ ( x ∗ ) ≠ 0 f'(x^*)\neq 0 f′(x∗)=0, f ( x ) f(x) f(x)在 x ∗ x^* x∗领域内有连续二阶导数,则由Newton迭代格式产生的迭代序列 { x k } \{x_k\} {xk}局部收敛于 x ∗ x^* x∗,并且收敛速度至少是平方收敛的(如果 f ′ ′ ( x ∗ ) ≠ 0 f''(x^*)\neq 0 f′′(x∗)=0,则收敛速度为平方收敛)。
可见,Newton法的收敛速度是较快的。定理1指出了Newton迭代法收敛的充分条件。在应用Newton法求方程的根时,应该在根 x ∗ x^* x∗的附近选取迭代初值 x 0 x_0 x0,以保证迭代过程的收敛性。在实际计算过程中,可以使用函数图像法来帮助确定迭代初值 x 0 x_0 x0。如果要想知道Newton法在根的分布区间 [ a , b ] [a,b] [a,b]上的收敛性,则应该使用下面的定理。
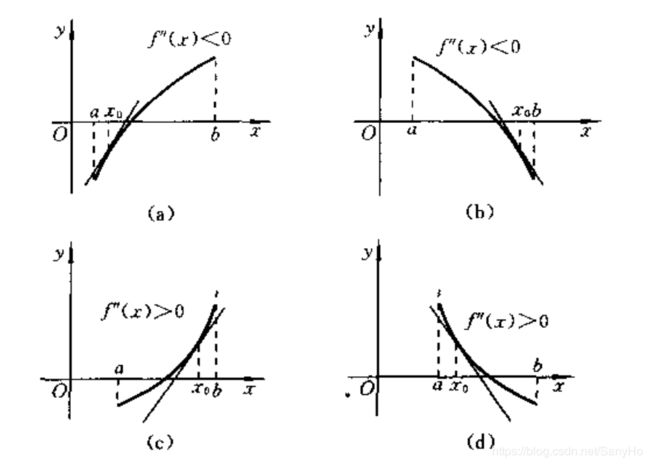
定理2:设 f ( x ) f(x) f(x)在区间 [ a , b ] [a,b] [a,b]上二阶导数存在,且满足:
(1) f ( a ) f ( b ) < 0 f(a)f(b)<0 f(a)f(b)<0
(2) f ′ ( x ) ≠ 0 , x ∈ ( a , b ) f'(x)\neq 0,x\in(a,b) f′(x)=0,x∈(a,b)
(3) f ′ ′ ( x ) f''(x) f′′(x)不变号, x ∈ ( a , b ) x\in(a,b) x∈(a,b)
(4) f ′ ′ ( x 0 ) f ( x 0 ) > 0. x 0 ∈ ( a b , ) f''(x_0)f(x_0)>0.x_0\in(ab,) f′′(x0)f(x0)>0.x0∈(ab,)
则Newton迭代公式收敛于 f ( x ) = 0 f(x)=0 f(x)=0在 ( a , b ) (a,b) (a,b)内的惟一根 x ∗ x^* x∗。
下图给出了满足定理2条件的几种情况。定理2的条件(1)保证根的存在性;条件(2)表明函数单调,根惟一;条件(3)表明函数的凹凸性不变;条件(4)保证当 x ∈ [ a , b ] x\in[a,b] x∈[a,b]时, φ ( x ) ∈ [ a , b ] \varphi(x)\in[a,b] φ(x)∈[a,b].
定理2的条件(4)也可表述为:
f ( a ) f ′ ( a ) < b − a , f ( b ) f ′ ( b ) < b − a \frac{f(a)}{f'(a)}
此时,对任意的初始近似值 x 0 ∈ [ a , b ] x_0\in [a,b] x0∈[a,b],Newton法均收敛于方程的根 x ∗ x^* x∗。
例2:求方程 e x − 5 x 2 = 0 e^x-5x^2=0 ex−5x2=0在区间 [ 2 , 5 ] [2,5] [2,5]上的根。
解:用图像法作出函数 f ( x ) = e x − 5 x 2 f(x)=e^x-5x^2 f(x)=ex−5x2的图像,如下图。很显然,方程在区间 [ 2 , 5 ] [2,5] [2,5]上有一单根。
(1)在根 x ∗ x^* x∗的附近选取迭代初值,用局部收敛性定理来判断迭代过程的收敛性。其二阶导数 f ′ ′ ( x ) = e x − 10 f''(x)=e^x-10 f′′(x)=ex−10在整个定义域内为一连续函数,故Newton法在该方程(全部)根的附近都具有局部收敛性。选取初值 x 0 = 4.5 x_0=4.5 x0=4.5,计算结果为 x ∗ = 4.7079379 x^*=4.7079379 x∗=4.7079379。如果不是在区间 [ 2 , 5 ] [2,5] [2,5]上靠近根的附近选取初值,就不能充分保证迭代过程收敛于根 x ∗ = 4.7079379 x^*=4.7079379 x∗=4.7079379。例如,选取初值 x n = 2.5 x_n=2.5 xn=2.5,则迭代计算结果就收敛于方程的另一个根 x k = 0.6052671 x_k=0.6052671 xk=0.6052671。
(2)用区间收敛性定理来判断迭代过程的收敛性。
由 f ′ ( x ) = e x − 10 x = 0 f'(x)=e^x-10x=0 f′(x)=ex−10x=0,得到函数在区间 [ 2 , 5 ] [2,5] [2,5]上的驻点 x 1 = 3.5771521 x_1=3.5771521 x1=3.5771521;由 f ′ ′ ( x ) = e x − 10 = 0 f''(x)=e^x-10=0 f′′(x)=ex−10=0,得到函数在区间 [ 2 , 5 ] [2,5] [2,5]上的拐点 x 2 = 2.3025851 x_2=2.3025851 x2=2.3025851。因此,在区间 ( x 1 , 5 ] (x_1,5] (x1,5]上; f ( x 1 ) f ( 5 ) < 0 f(x_1)f(5)<0 f(x1)f(5)<0;对于任意的 x ∈ ( x 1 , 5 ) x\in(x_1,5) x∈(x1,5),始终有 f ′ ( x ) > 0 f'(x)>0 f′(x)>0和 f ′ ′ ( x ) > 0 f''(x)>0 f′′(x)>0。所以为满足 f ′ ′ ( x 0 ) f ( x 0 ) > 0 f''(x_0)f(x_0)>0 f′′(x0)f(x0)>0,必须使初值 x 0 ∈ ( x ∗ , 5 ] x_0\in(x^*,5] x0∈(x∗,5]。如果即取 x 0 = 5 x_0=5 x0=5,则能充分保证迭代计算结果收敛与根 x ∗ x^* x∗。但如果取 x 0 = 3.7 ∉ ( x ∗ , 5 ] x_0=3.7\notin (x^*,5] x0=3.7∈/(x∗,5], f ′ ′ ( x 0 ) f ( x 0 ) > 0 f''(x_0)f(x_0)>0 f′′(x0)f(x0)>0是否成立?又会有什么样的迭代计算结果?
- 初值的选取方法
应用Newton法求方程的根,选择初始值 x 0 x_0 x0很重要,如果 x 0 x_0 x0取得偏离所求方程的根较远,就可能使迭代过程发散或增加迭代次数。但是,根据Newton法收敛性定理来选取初始值,往往有比较复杂。为此,通常可以采用下面的简化方法:
对于方程 f ( x ) = 0 f(x)=0 f(x)=0,如果
f ′ ′ ( x 0 ) ≠ 0 , ∣ f ′ ( x 0 ) ∣ 2 > ∣ f ( x 0 ) f ′ ′ ( x 0 ) 2 ∣ (2) f''(x_0)\neq 0, \quad |f'(x_0)|^2>|\frac{f(x_0)f''(x_0)}{2}| \tag{2} f′′(x0)=0,∣f′(x0)∣2>∣2f(x0)f′′(x0)∣(2)
则可以保证在大多数情况下Newton迭代过程的收敛性。
例3:用Newton法求 x 3 − x − 1 = 0 x^3-x-1=0 x3−x−1=0在 x 0 = 1.3 x_0=1.3 x0=1.3附近的一个根。
解:原方程的Newton迭代格式为 x k + 1 = x k − x k 3 − x − 1 2 x k 2 − 1 x_{k+1}=x_k-\frac{x_k^3-x-1}{2x_k^2-1} xk+1=xk−2xk2−1xk3−x−1,选取 x 0 = 1.5 x_0=1.5 x0=1.5,迭代结果为:
x 1 = 1.34783 , x 2 = 1.32520 , x 3 = 1.32472 , x 4 = 1.32472 x_1=1.34783,\quad x_2=1.32520, \quad x_3=1.32472, \quad x_4=1.32472 x1=1.34783,x2=1.32520,x3=1.32472,x4=1.32472
即迭代4次,有6位有效数字。
如果迭代初值取为 x 0 = 0.6 x_0=0.6 x0=0.6,则迭代计算结果如下:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sRusrebJ-1590499188369)(/Users/can/Library/Application Support/typora-user-images/image-20200520172406248.png)]
即需要迭代11次才能达到计算精度的要求。
例4:求方程 f ( x ) = x 3 − 2 x − 5 = 0 f(x)=x^3-2x-5=0 f(x)=x3−2x−5=0在 x 0 = 2 x_0=2 x0=2附近的实根。
解: [ f ′ ( 2 ) ] 2 = 100 , f ( 2 ) f ′ ′ ( 2 ) = 6 [f'(2)]^2=100,\,f(2)f''(2)=6 [f′(2)]2=100,f(2)f′′(2)=6,有:
[ f ′ ( 2 ) ] 2 > [ f ( 2 ) ⋅ f ′ ′ ( 2 ) ] / 2 [f'(2)]^2>[f(2)·f''(2)]/2 [f′(2)]2>[f(2)⋅f′′(2)]/2
所以可以用 x 0 = 2 x_0=2 x0=2作为初始值。迭代结果为
x 1 = 2.1 , x 2 = 2.09457 , ⋯ , x = 2.09455 x_1=2.1, \quad x_2=2.09457,\cdots, x=2.09455 x1=2.1,x2=2.09457,⋯,x=2.09455
如果选取 x 0 = − 2 x_0=-2 x0=−2作为初值,虽然不能满足(2)式的条件,但计算结果还是收敛于方程的根,只不过是迭代次数有所增加。下图表示了 x 0 = − 2 x_0=-2 x0=−2的迭代计算过程。