多元线性回归方程建模：使用岭回归与lasso算法选择变量

前言：

    本文是作者学习机器学习多元线性回归部分，就消除多重共线性、选择变量问题而做的练习。参照了《R-modeling》.薛毅.P331 例6.10例子，使用到R语言的MASS包，ridge包，lars包。

《R-modeling》.薛毅  http://download.csdn.net/detail/solomon1558/8229859

例6.10 某种水泥在凝固时放出的热量Y（卡/克）与水泥中四种化学成分X1，X2，X3，X4有关。现测得13组数据，如下表所示。希望从中选出主要的变量，建立Y关于它们的线性回归方程。

1 多元线性最小最小二乘法估计

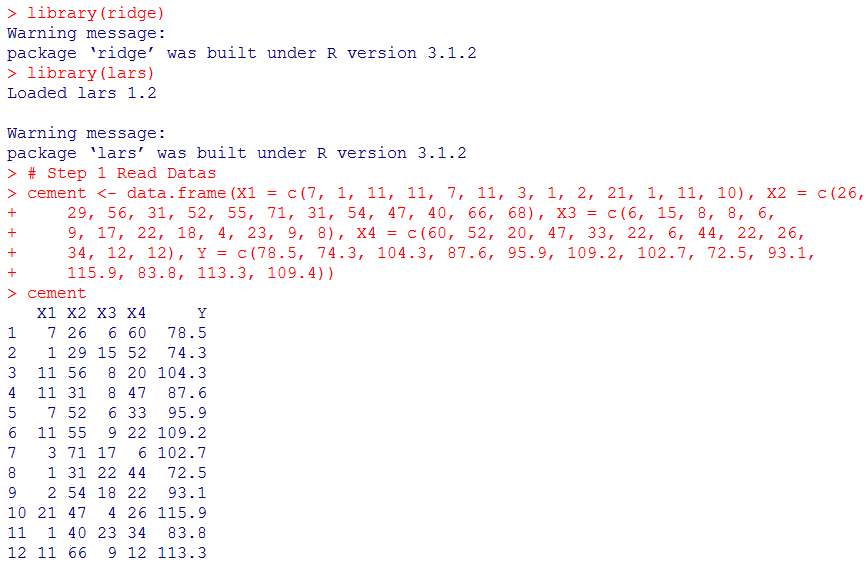
1.1 读入数据

1.2全部变量参与线性回归

    根据观察，截距与变量均不能通过系数检验，并且残差较大。

   

1.3 样本多重共线性检查

求解样本方阵的条件数(kappa值) ，kappa =2009.756,易知kappa1000,变量间具有严重的多重共线性。

2. 利用MASS包中的lm.ridge实现岭回归

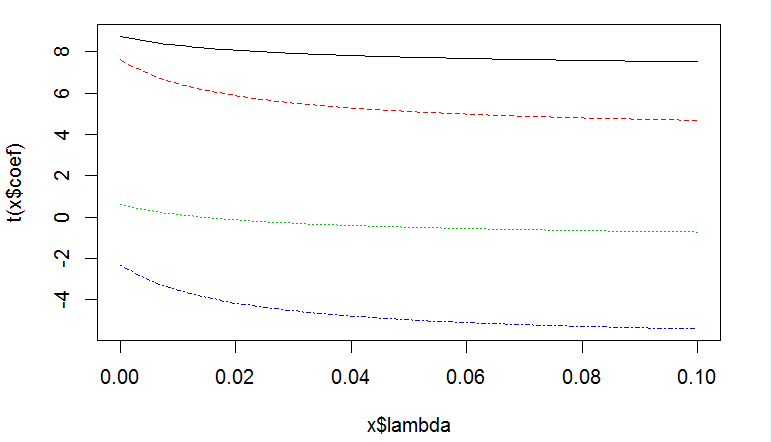
2.1  k取值[0,0.1],步长0.001.求解不同k值下的岭回归估计族。

    观察岭迹图，结合X1、X2、X3、X4各变量k[0,0.1]上的系数β值，发现X3的系数绝对值始终很小，而且从正穿越到负，故舍去变量X3。

2.2 作Y与X1、X2、X3的多元线性回归模型，发现变量X3系数检验不过关，舍去变量X3.

2.3 舍去变量X3、X4后，使用select函数对该模型求解lambda值

    取GCV的值lambda = 0.082。

    将lambda值代入线性回归模型，得到对因变量Y有偏的估计

    Y^ = 52.577 + 1.4683X1 + 0.6622X2.

     这个结果与薛毅书中P335页例6.10结果相近。

3 使用ridge包求解岭参数lambda

3.1 键入以下命令：

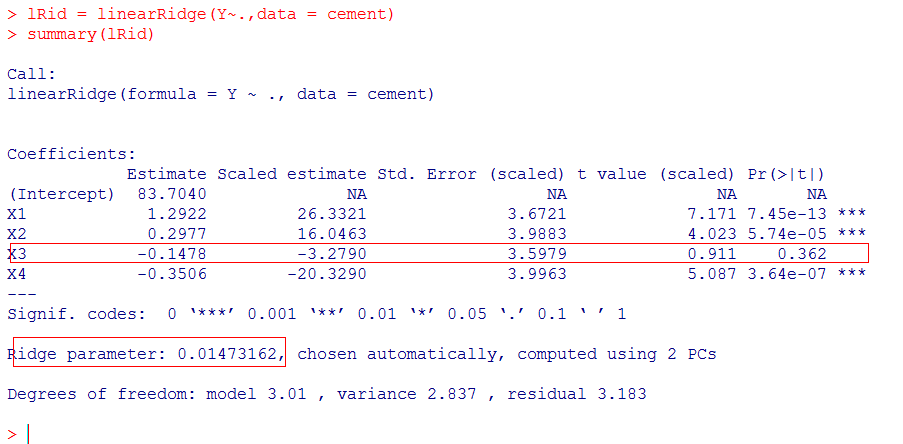
> lRid = linearRidge(Y~.,data = cement)

> summary(lRid)

    得lambda = 0.0147。

    据观察，变量X3的系数没有通过检验，应该舍去。

3.2 去掉X3后再做岭回归

得lambda = 0.005856，据观察变量X4没有通过系数检验，故应舍去。

3.3最终的回归模型：

lambda = 0.004852

Y^ = 52.5749 + 1.4629X1 + 0.6595X2.

 

4    使用采用lasso构造多元线性回归模型

4.1 变量选择次序

> lar =lars(cementMat[,1:4],cementMat[,5])

> lar

Call:

lars(x = cementMat[, 1:4], y = cementMat[,5])

R-squared: 0.982

Sequence of LASSO moves:

    X4 X1 X2 X3

Var  4  1  2  3

Step 1  2  3  4

        由此可见，LASSO的变量选择依次是X4，X1，X2，X3

 

4.2  summary(lar)

>summary(lar)

LARS/LASSO

Call: lars(x =cementMat[, 1:4], y = cementMat[, 5])

  Df        Rss           Cp

0  1       2715.76    442.9167

1  2       2219.35   361.9455

2  3       1917.55    313.5020

3  4       47.97       3.0184

4  5       47.86      5.0000

    由以上信息可知，在第三步cp指标(Mallows’s Cp)值最小,且残差RSS和比较小。
    第三步的结果是x4, x1, x2变量，所以最终的变量选择是x4, x1, x2变量
    根据得到的结果，我们可以做进一步的线性回归分析。

5. 总结

    岭回归和lasso的适用场景是特征项非常多或者特征间存在多重共线性的情况。岭回归与Lasso都采用了“增加惩罚函数”的方法来判断、消除多个特征间的多重共线性。其中岭回归主要用于判断、消除特征间的多重共线性，较少用于变量剔除，而Lasso可以用于解决多重共线性问题以及剔除变量。同时，两者都是对总体的有偏估计。

    因为岭参数lambda不是唯一确定的，所以岭回归估计β^(k)实际上是回归参数β的一个估计族。求解岭回归的重点是确定解岭参数lambda。可以借助岭迹图，或是方差扩大因子法等计算方法求解lambda。

    因为lambda的确定方法多种多样且结果相差巨大，因而岭回归的结果存在争议，现已不再广泛使用。

    Lasso全名The leastAbsolute shrinkage and Selectionator operator（最小绝对(值)收缩和变量选择),Tibshirani于1996年提出。通过构造一个一阶惩罚函数获得一个精炼癿模型；通过最终确定一些指标（变量）癿系数为零（岭回归估计系数等于0癿机会微乎其微，造成筛选变量困难），解释力很强。

    但是因为惩罚函数是一阶带绝对值的函数，故约束域的角尖处不可导，不能求偏导，用微积分的方法做无解。需要用很复杂的数值计算求解回归方程，算E法复杂度很高。

    直到Efron于2004年发现LAR（Least Angel Regression）算法所描述的回归问题求解过程与Lasso的求解过程几乎一致，可以通过LAR算法高效的地求解Lasso回归，才使得Lasso算法得到学术界的重视。

    LAR算法类似于向前逐步回归(Forward Stepwise),两者区别在于：LAR是每次先找出和因变量相关度(夹角余弦值)最大的变量，在保证残差向量与当前选入变量的相关系数一致的路径方向上前进，直到最终包含所有变量，且变量与残差向量的相关系数为0，即求得最小二乘解的估计。

    如今，使用LAR算法求解Lasso，从而消除特征之间的多重共线性和选择变量已经成为了一种常用的方法。