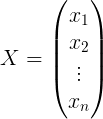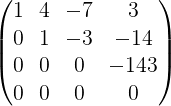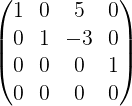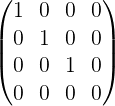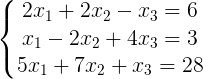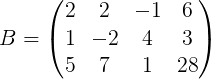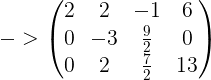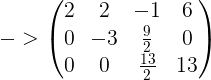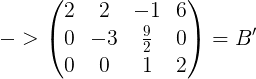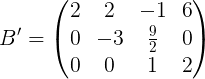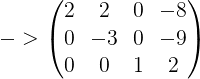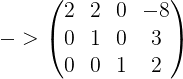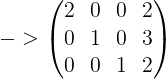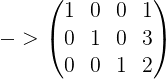【矩阵】高斯消元

参考博客：

luogu P3389 【模板】高斯消元法

线性方程组（高斯消元）f_zyj

高斯消元—kuangbin

解线性方程组——高斯消元の板子

---

高斯消元：

【前置知识】:

高斯消元有一个很重要的应用就是求解线性方程组：

线性方程组:（特指n个变量）n个n元一次方程方程组

转化为矩阵，按照x1～xn排列，对应的值为b1～bn.

---

可以转化为矩阵：

           

其中，A叫系数矩阵，X为解集，b是常数项

以上线性方程组可以写成：

AX=b，满足矩阵乘法，X的每一列 元素  对应  乘以A中每一行上面；

 

增广矩阵：在原矩阵的基础上增加   增加列（行）【前提是：这个矩阵的行（列）数相同】

矩阵的初等变换：

1、交换矩阵的两行（交换i,j两行，记作 ）

2、以一个非零的数k乘矩阵的某一行（第i行乘数k，记作）

3、把矩阵的某一行的k倍加到另一行（第j行乘数k加到第i行）

其中初等变换有行变换和列变换，以上都是行变换，可以统一改成列变换。

---

区分：

对于计算行列式的话，行列变化可以混用。但是那个不叫矩阵初等变换，叫行列式的性质

对于化简矩阵，求矩阵的秩，可以使用行列变换，但是只能统一使用行，或者统一使用列变化。

对于求解线性方程组的解集等，都是用行变换居多。

---

行阶梯型矩阵：

满足两个条件

（1）零行（元素全为0的行）位于矩阵的下方。

（2）各非零行的首非零元（从左到右的第一个不为零的元素）的列标，随着行标的增大而严格增大（或说其列标>=行标）

什么意思呢？（以下矩阵都是行阶梯型矩阵）

   

行最简形矩阵：

   

标准形：（进行列变换，左上角为单位矩阵，其余全为0）

---

高斯约当消元的过程：

就是化简行阶梯型矩阵的过程，但是还有一些细节地方。

正所谓一图胜千言，我就拿《线性代数》-（中国人民大学出版-理工类 第五版)P93例题解释：

---

消元过程：

转化为增广矩阵B=(A b)：

 

---

回代过程：

消元到最后一行，观察，对于原方程：解得：

  代入消元后的B‘矩阵的第二行，解得：

把，  代回第一条方程：

解得：

这是大家手动实现的，但是放在矩阵里还没有算完。

 

 

---

 

主元  数学概念

参考博客：高斯消元法（高斯·约当消元法）（浮点）

【算法实现】：

针对n个方程，n个未知数的方程组来说。

伪代码：

For 枚举每一列：

       找最大的行进行交换（操作叫：列换主元）

       特判对于这一位上是否

#include
using namespace std;
const int N=115;
const double eps=1e-7;
double a[N][N]; //增广矩阵(A b)
double x[N];    //解集
int n;
void Gauss_Jordan(){

    for(int col=1;col<=n;col++){
        int row=col;
        for(int i=row+1;i<=n;i++)   //选择对应列上最大值，更新下标
            if(fabs(a[i][col]-a[row][col])>=eps)
                row=i;
        if(fabs(a[row][col])<=eps) {
            printf("No Solution\n");
            return ;
        }
        //列换主元
        if(row!=col)    swap(a[row],a[col]);

        row=col;        //交换后，row返回对角线

        //对角线位置系数化为1
        //double K=a[row][col];
        //for(int j=col;j<=n+1;j++) a[row][j]/=K;

        //消元过程：
        for(int i=row+1;i<=n;i++){  //讨论对角线以下的位置
            if(fabs(a[i][col])<=eps) continue; //该位置为0，不作处理

            double K=a[i][col]/a[row][col];  //计算出首元素的比例
            for(int j=col;j<=n+1;j++)
                a[i][j]=a[i][j]-a[row][j]*K; //减去对应位置*比例

        }
    }
    //回代过程：
    //对第n条方程算出的第n个未知数开始回代，
    for(int i=n;i>=1;i--){
        x[i]=a[i][n+1];
        for(int j=i+1;j<=n;j++){
            x[i]=x[i]-a[i][j]*x[j]; //减去已解出来的未知数乘以对应的系数
        }
        x[i]=x[i]/a[i][i];          //别忘了，还需要把对应位置系数除去
    }
    for(int i=1;i<=n;i++){
        printf("%.2lf\n",x[i]);
    }

}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n+1;j++)
            scanf("%lf",&a[i][j]);

    Gauss_Jordan();
    return 0;
}