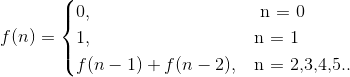《程序员的数学6:递归》
本文属于《程序员的数学》读书笔记系列。递归是“自己定义自己”。可能说道递归首先想到的例子是阶乘。但是作者从汉诺塔的例子开始介绍,再试阶乘,帕斯卡三角形,学习从复杂逻辑找出递归结构。
汉诺塔
汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。上面是百科的内容。
我记得初次接触这个,应该是在大学的数据结构,现在再看看,结论不重要,思维方式更重要。
书上是简化了,举个6片的例子。当然,只看文字描述容易产生歧义,尤其是第一次看的时候不容易理解。加个图就好多了
先从3个圆盘开始,参见上面的动图。
先缩小范围,移动7次即可。记下每步,找规律。
在1,2,3步中,用了3次吧2个圆盘从A柱移动到C柱。
5,6,7 步中,用了3次吧2个圆盘从C柱移动到B柱。
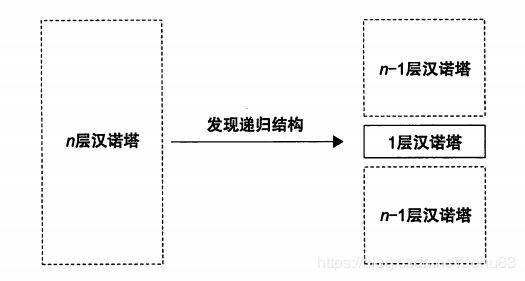
同样的思路可以求出,6层就是先解出5层的汉诺塔A->C,在移动最大的圆盘A->B,再解出5层的C->B。要解出6层的就要用到“5层的汉诺塔解法”,同理,5层4层3层。。。,1层汉诺塔只要移动一个圆盘就行。
通过这种思考方式,我们可以得出“n层的汉诺塔的解法”。
将n个圆盘从X柱,经由z柱周转,转移到y柱时:
当n=0, 不做任何操作。
当n>0时,
- 首先把 n-1圆盘从X柱经Y柱中转,移动到Z柱(解出n-1层汉诺塔)。
- 然后,把1个圆盘从X柱转移到Y柱。
- 最后,把n-1个圆盘从Z柱,经过X柱中转,转移到Y柱(解出n-1层汉诺塔)。
那么,我们用H(n)表示所需要的最小次数。
H(0) =0, H(1 )=1
我们把移动次数H(n)的式子写成
我们把这种H(n)与H(n-1)的关系式称为递推公式。
求出解析式
从上面的H(n)的公式,可以求出结果。也就是如下表示:
0,1,3,7,15,31,63.。。
找规律就是H(n)= ![]()
这种只用n 表示H(n)的式子叫做解析式,可以用数学归纳法来证明 该解析式的正确性。
使用程序表示
public class HannuoiTest {
static int i=0;
public static void hannuoi(int n,String x, String y,String z){
if(n==0){
}else{
hannuoi(n-1,x,z,y);
System.out.println(x+"->"+y);
hannuoi(n-1,z,y,x);
i++;
}
}
public static void main(String[] args) {
hannuoi(6,"A","B","C");
System.out.println(i);
}
}输出结果:
A->C
A->B
C->B
A->C
B->A
B->C
A->C
A->B
C->B
C->A
B->A
C->B
A->C
A->B
C->B
A->C
B->A
B->C
A->C
B->A
C->B
C->A
B->A
B->C
A->C
A->B
C->B
A->C
B->A
B->C
A->C
A->B
C->B
C->A
B->A
C->B
A->C
A->B
C->B
C->A
B->A
B->C
A->C
B->A
C->B
C->A
B->A
C->B
A->C
A->B
C->B
A->C
B->A
B->C
A->C
A->B
C->B
C->A
B->A
C->B
A->C
A->B
C->B
63
回归到汉诺塔问题,我们使用了“n-1”层 汉诺塔,来表示n层汉诺塔来考虑问题。
"能将复杂问题转换为较为简单的同类问题吗? "这就是递归的思维方式。
先从问题中找出递推结构,如果找出了递推结构,接下来就是根据递推结构建立递推公式。
汉诺塔的问题先到这里,我们带着“找出递推结构”的思路,看下一节。
阶乘
我们上一章介绍过,n! = n*(n-1)*(n-2)*....*2*1;
之所以将它称为递归定义是因为“它使用了阶乘(n-1)来定义阶乘n! ”,
对于n>0 的任意整数,N! 定义都和明确,不会循环无解,因为0!= 1.
思考题:
请用递归方式定义0....N的整数之和,就是之前介绍过的高斯断言。
斐波那契数列
如果一开始有一对兔子,它们每月生育一对兔子,小兔在出生后一个月又开始生育且繁殖情况与最初的那对兔子一样,那么一年后有多少对兔子?
每月兔子的总数可以用以下数列表示:1,1,2,3,5,8,13,21,34,55,89,144,233 …
这一数列是意大利数论家列奥纳多·斐波那契(Leonardo Fibonacci)发现的。
递归公式如下:
,数学上有很多有关的,黄金比例就与此有关。自然界还有很多复合的,如鹦鹉螺(一种海螺)壳,葵花种子排法等等。
看下Java的实现方法:
public class FribNumTest {
public static int fib(int num) {
//判断:是否是第一个数和第二个数
if(num == 1 || num == 2) {
return 1;
}else {
//递归调用
return fib(num - 2) + fib(num - 1);
}
}
public static void main(String[] args) {
for(int i = 1;i <= 11;i++) {
System.out.println(fib(i) + "\t");
}
}
}
输出:
1
1
2
3
5
8
13
21
34
55
89
剩下的帕萨卡三角,作者用组合![]()
![]() 来介绍的,没看懂,后面在整理吧。
来介绍的,没看懂,后面在整理吧。