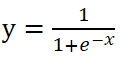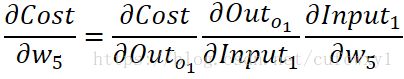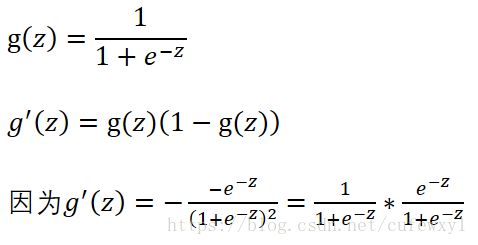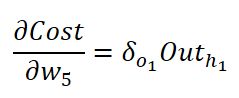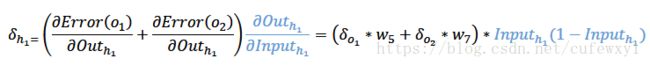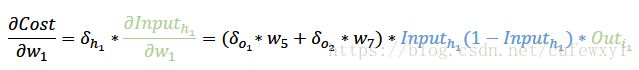BP神经网络（BPNN）

本文简要介绍BP神经网络（BPNN, Back Propagation Neural Network）的思想。

BP神经网络是最基础的神经网络，其输出结果采用前向传播，误差采用反向（Back Propagation）传播方式进行。BP神经网络是有监督学习，不妨想象这么一个应用场景：输入数据是很多银行用户的年龄、职业、收入等，输出数据是该用户借钱后是否还贷。作为银行风控部门的负责人，你希望建立一个神经网络模型，从银行多年的用户数据中学习针对银行客户的风控模型，以此判定每个人的信用，并决定是否放贷。

基本结构

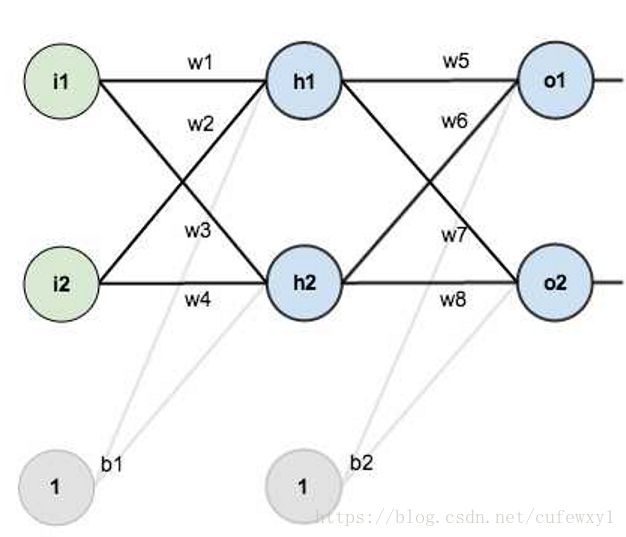
模仿人类的神经元激活、传递过程（还记得高中生物的“突触”这个概念嘛）。以三层神经网络为例，BP神经网络含输入层、隐含层、输出层三层结构。输入层接收数据，输出层输出数据，前一层神经元连接到下一层神经元，收集上一层神经元传递来的信息，经过“激活”把值传递给下一层。

以上图为例，i是输入层(Input)，h是隐含层(Hidden)，o是输出层(Output)，w是权重，b是“偏置”，偏置的作用在下文中会详述。每个圆圈都是一个神经元。

前向传递

w是连接前后两层神经元的权重，例如h1的输入就是前一层神经元输出的加权之和（再加上偏置），即i1*w1+i2*w2+b1*1

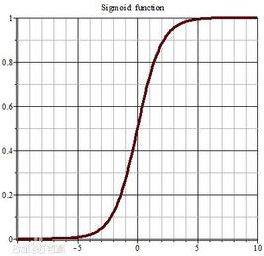
h1的输出是对这个输入的“激活”。激活是一个非常神秘，具有生物色彩的名词，模型里激活是以激活函数的形式体现的，比如常用的激活函数是Sigmoid函数

这个函数有两个特点符合生物学里的神经激活：

1. 单调递增，保证输入的信号越大，激活后的输出信号越大

2. 值域是(0, 1)，相当于把定义域(-∞，+∞)映射到(0, 1)信号，毕竟激活函数的作用就是把范围较广的数限定到0-1的信号中往下传递

所以h1的输出就是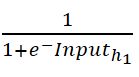其中Input就是刚刚所述的加权之和。h1的输出再经过与h2输出的加权求和传递到o1、o2，再进行激活就成为整个网络的输出。

总结一下，这里用Sigmoid模仿神经元之间的传递，将范围很大的数限定到0到1之间，作为信号往后传递，每层神经元接收上一层神经元的信号，在自己这里激活，传到下一层神经元。

反向误差传播

一般我们会随机初始化权重和偏置。把样本数据传入到网络，输出与实际值比较就能看到模型误差有多大了。由于我们随机初始化参数，可以说这种参数设定十分随意，不可能第一次就能把这个模型确定，必须有一个“学习机制”，让模型的参数不断优化逼近到最佳的状态。

这里涉及到梯度的概念。如果对梯度不熟，可以参考一下斜率。想象一下，如果我们在山脚，希望爬到最高峰，那么每次在自己位置环顾一周，找到海拔上升最高的方向（斜率最大），沿着这个方向走一步以后再环顾一周……这样循环下去，最终会爬到一个高峰（也许不是最高峰，但周围一定比这个点海拔低）。与此类似，BPNN要找到误差最小的参数，就要根据负梯度方向寻找误差的最小值。

我们表示出误差的式子，然后将这个误差对参数求导数，让参数沿着负梯度方向变化，不断循环直到参数变化不大，那么我们可能就处于一个误差比较小的点了。

误差表示为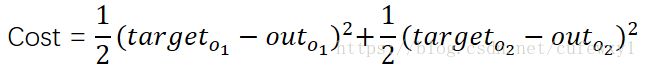其中target指实际值（目标值），out指神经网络的输出值。之所以前边有1/2系数是因为待会求导的时候，括号的二次方与1/2抵消。

因为这里有两个输出，所以需要将两个输出的误差加起来。误差的形式采用差的平方，这也好理解，输出值与实际值差别越小，说明我们的模型越厉害，误差就越小；否则误差越大。取平方是因为有负数的情况。在机器学习中损失函数(Cost function)是个很通用的概念，顾名思义它是对模型的“惩罚”，这里实际上就是误差，误差越大我们对模型的惩罚越大。

误差表示好之后，我们就要求导数了。这里的参数包括权重和偏置。所以要求损失函数对权重和偏置的导数。

从后往前看，首先分析损失函数对w5的导数。根据求导的链式法则，可以把中间变量写出来：

等式右边第一项，根据损失函数的形式，可以知道是。第二项是Sigmoid函数的导数。Sigmoid函数的导数有个性质，结果=函数值*（1-函数值）。例如g(z)是Sigmoid函数

所以等式右侧第二项等于

等式右侧第三项比较简单，因为Input是输出值的加权求和，所以Input对权重w5的导数就是h1的输出值

在吴恩达老师Coursera的课程里，会把等式右侧前两项合并为，表示误差传播到o1这个节点时候的误差，表示节点对于最后误差负的责任。然后从o1再往上一层传播到h5，即乘以等式右侧最后一项，就是最终结果

即

注意这个δ，虽然在这里不太起眼，但是在后边推导更高级神经网络（LSTM等）的时候帮了大忙。

对偏置的求导就比较简单了，是先传播到o1的节点，得到。当再传播到偏置的时候，加权求和时候偏置前的系数为1，所以结果依然是自身。所以结果就是。

对于再往前的权重w1，可以先求

注意既影响了o1的误差，又影响了o2的误差，所以对他的导数有两部分

故

总结一下

参数（包括权重、偏置）一开始是随机初始化的，具有不确定性，反向传播是为了让模型的参数接近最佳值；

反向传播是基于梯度的，类似爬山时候寻找四周上升速度最快的方向；

求导基于链式法则，找到这个权重（或偏置）是怎么影响最终的误差的，是否影响多个输出值误差；

可以定义一些，表示误差传播到节点（神经元）时的结果，表明这个节点对最终误差所负的责任。节点再往前推导权重、偏置就比较容易了：如果是对权重求导，就要乘上权重连接末端输入对权重的偏导，实际等于该权重所连接起点神经元的输出（这话比较绕，见上式）；如果是偏置，则结果就是该。

后记

对于作者来说，最让人兴奋的是，人类只不过用几个元件模拟了人脑的运作模式，而且并非完全模拟（脑神经科学依然在发展，且这种反向传播并非人类所使用的模式，如Hinton提出了胶囊改进），但是效果却出奇得好。人类只不过搭好了架子，不断喂数据，这个架子自己就能学习到相应的知识，并在样本外数据有时依然work，这大概是最吸引人的地方。

还有很多细节的问题，例如：

1. 梯度消失。激活函数Sigmoid的导数在0达到最高，只有0.25<1，当隐含层有很多层时候，用链式求导法则求靠前位置的倒数，连乘的时候结果越来越小，可以换用ReLU等形式激活函数

2. 损失函数的其他形式。首先可以加上正则项（不影响本文理解），其次有其他形式的损失函数，例如吴恩达老师在Cousera的课程中有一页PPT用的是对数形式的损失函数，例如实际值y=1，那么out=1时候损失函数结果为0，如果out=0损失函数就无限大了，这种形式是基于极大似然思想。在b站上有的弹幕表示后边内容没看懂，如果知道损失函数是这种形式，后边就好推了。

参考资料

1. 吴恩达Coursera机器学习课程

2. https://blog.csdn.net/treasuresss/article/details/50809148