上回书说到 -
一个小组的同学 (6-8 人) 决定要徒步遍历中国陆地边界, 假设供给装备齐全, 估计需要多长时间?
用什么样的办法能让同学们方便地交流各自的估计, 最后到达大致理性和统一的共识?
一般这个时候教室里一定非常热闹, 大家各抒己见, 争执得不亦乐乎。 但是最后往往谁也说服不了谁, 还有一些同学无动于衷, 觉得无从下手, 干脆不参加讨论。 在这种情况下, 可以考虑通过 Wide-band delphi 来达到快速沟通和达到意见的一致。
网上有不少关于这类方法的介绍:
http://www.stellman-greene.com/aspm/content/view/23/38/
http://en.wikipedia.org/wiki/Wide-band_delphi
http://drdobbs.com/article/printableArticle.jhtml?articleId=184414570&dept_url=/ (Dr. Drobb’s)
这个方法看起来复杂, 其实挺简单的:
1) 找到一个主持人 (facilitator/moderator)
2) 主持几轮讨论, 每一轮统计大家的估计, 并且询问大家估计值的前提假设是什么, 找到合理的假设, 然后继续。
例如: 第一轮, 大家的估计和假设是:
a) 300 年 假设: 要按照边界走, 爬到珠穆朗玛峰就挂了
b) 2 年; 假设: 两万多公里的陆上边境线。参考红一方面军在长征时候的记录,12个月走1万两千公里。所以2年即可。
c) 5 年; 假设: 3 万公里, 一年工作 300 天, 每天20公里,
d) 1 年; 假设: 边界大概有10个省份, 每个省份在当地公安边防的带领下, 一个月就搞定了。 有两个月用于和各地政府取得联系。
e) 5 个月 假设: 南宋后再无中国, 只好沿着南宋的边界走, 走走玩玩, 很快就走完了。
f) 不可能 假设: 被有关部门请去喝茶
[我在微博上看到还有人说 50 天的, 不知道他的假设是什么样子…]
…
大家对各自的假设做了分析, 得出了新的共同假设:
沿着边界 = 离边界最近的公路或小路走, 青藏高原可以绕一下, 不必亲自到每一块界碑跟前拍照留念。 不过还得自己走。
陆地边界 = 中国现在的边界, 不是南宋的。 约等于2 万公里
在这样的前提下, 大家又有新的一轮估计:
… …
然后又澄清一些假设,
… …
最后大家的估计收敛到一个大家都比较满意的精度数值。于是估计就结束了. 注意在精度上, 大家不必太拘泥, 根据这个题目的情况, 用月做单位即可。 不必争论到底会用 1002 天还是1003 天。
主持人要记住在每一轮的估计中, 探询数值背后的假设, 这是作为项目经理最重要的能力. 另外, 要推动数值收敛, 这要求大家的假设 (也就是用户需求分析) 也要收敛, 不要天马行空。在每一轮的讨论中, 估计值的上界和下界要不断接近。
注意, 最后得到的估计数值, 也许和某人最初提出的数值很接近, 但是这意义并不大, 因为最后达成的假设也许和最初的假设大相径庭。 Wide-band delphi 的目的不是比谁的第一轮估计猜得准, 而是在较短的时间内让团队充分沟通, 交换意见。
在这个练习中, 很重要的一点是要估计团队自身的能力, 你看到别人能每天行军30公里, 你自己未必能够。 你听说编程大牛几天写好某模块, 你自己却花了几个星期。 在上课的时候, 有同学提到团队要先培训几年, 这也是很好的角度, 在开始使用一个全新的技术前, 一段时间的培训和练习是很有必要的。 你的估计中是否包括这些因素?
还有一个高级PM能考虑到的问题, 既然这是一个长期项目, 那不可避免地有人员的投入 (commitment)和变动 (attrition) 问题。 大家走着走着, 有人受伤怎么办? 有人和当地少数民族少女坠入爱河怎么办? 有人打退堂鼓怎么办?
软件开发的一个特点是, 软件项目的确有不少东西可以重用别人的结果, 但是项目中最有价值的部分, 别人都还没做过, 还得自己动手. 这就要求我们去探索, 发现这样的工作到底需要多长时间。 问题是 - 探险者总是高估自己的能力,低估未知的困难 - 不然他们就不会出门探险了!
据说, 早期的西班牙探险者到美洲达科罗拉多河大峡谷的时候, 他们站在峡谷南岸俯瞰深谷中蜿蜒的河流, 觉得那不过是一条细细的小溪而已。 队长估计用不了一天的时间就能跨越, 于是大队人马开始出发。 等他们下到山谷的一半, 才发现河流湍急, 自身的装备不够, 人困马乏, 只好又悻悻返回, 同时已经累得半死。
我们在做项目的时候, 也有很多次发现原来估计很容易的地方原来 “水很深”, 往前走, 也许会被淹死, 往回退, 会耽误大量的时间。 这时候大家心里都暗想 - 当时要是在项目计划的时候多做深入分析和估计就好了! 但是回过头来, 对于这种情况, 大家如果坐在峡谷边 wide-band delphi 一整天, 也依然会得出非常乐观的结论,因为没有人提出不同的 “假设”。 这时候, 我们可以考虑参考前人的经验, 打听一下当地人跨越大峡谷要几天。
团队软件开发活动是有个人的活动构成,但并不是简单的延伸。 年轻人跑一千米需要多少准备? 几乎不用,穿上鞋就跑好了。那么,跑一个马拉松是不是 "同理可证” 呢?
请看这个照片,为何会出这样的问题?
换到软件开发的场景中, 我们可以设想, 你和某个同事在合作上有一些不顺, 有一些小摩擦;或者软件工具和环境没有配置好,就像鞋子里进了沙子,不太舒服... 如果是合作一个半天的小项目, 那没啥大不了的。 但是如果是做一个几个月的项目, 这些小摩擦,小沙子不预防,不处理就会导致大问题。 我们在估计项目难度的时候,考虑到这些问题了么?还是简单地线性推断工作量?
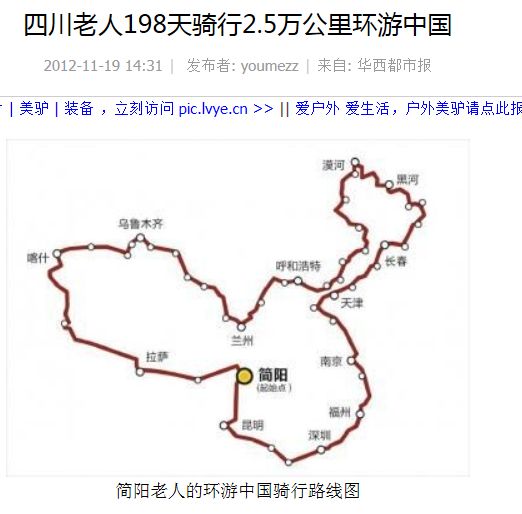
有些事情花的时间是客观规律, 不是由个人能力决定。 例如人类生一个小孩大约需要10个月, 这个估计和你的 S 是大号, 中号, 还是小号无关, 和婚礼来宾的数量也无关。 要是还不满意怀孕时间长, 再加上几个精壮男子帮忙, 也无济于事。 世界上很多事情都有人做过了, 即使和你的具体情况有种种区别, 还是可以作为参考, 例如你想徒步走遍全国, 貌似前无古人, 但是不妨看看一个骑自行车走遍全国的例子:
[链接: http://www.lvye.cn/article-26533-1.html]
这些老人骑车用了大约200天, 小伙子走路能比他们快么? 另外, 老人们走的是城市间的连接线, 大学生们要走边境线, 难度比较一下, 原来那些小于300 天的估计都可以推翻了。
另外一个办法是快速原型法 - 用一两个先锋去探路。 例如一个项目如果能用上 Microsoft Azure 平台, 那貌似会给我们带来很多好处. 如果你光看 Azure 的宣传资料, 你觉得这简直太容易了, 咱们赶紧上马! 且慢, 这时不妨派一个人写一个简单的Azure Hello World 应用, 实际看看开发/调试/部署/支持的情况如何, 这样才能给项目估计提供更好的数据支持。
我自己在长期的革命斗争中, 摸索出一套经验公式: 你问一个开发人员两件事 – 对某件事的估计时间 X, 以及他做过类似开发工作的次数 N. 那么他最终需要的时间
Y = X +/- X/N //注: 中间的 +/- 表明或者加上, 或者减去。
例如果冻估计某个模块需要 3 天, 但是果冻从来没有做过, 那么这件事情实际花费的时间有两种可能 Y = 3 +/- 3/0.
就是说, 这事情也许是 (3 + 无穷大), 在项目时间内压根就做不了。 例如一个学生团队一度想做 “用玩家的人脸做拳皇游戏”
或者是 (3 - 无穷大), 不但不用做, 而且这个员工会搞出很多新的bug 来, 让团队花更多的时间来处理, 把项目拖垮.
比如果冻说要实现网络用户的管理, 结果发现Asp.net 早就实现了. 但是果冻不服,非得要自己写一个。 结果写得漏洞百出, 很多其他员工来帮他擦屁股。 最后把他的代码扔了, 用标准控件来实现。
当 N 等于 1 的时候, 一项工作估计的实际花费范围是 [0 .. 2X], 如果员工一直做类似的项目, 他们的 N 值都在 1 以上, 估计变化的范围会越来越小, 准确度越来越高。当然, 技术在变, 市场在变, 员工的心态也在变, 员工是不甘于, 也不能一直做雷同的项目的。
如果把这个公式展开一下, 项目的复杂程度
a) 需求的复杂程度 - 程序员是第几次实现类似的需求? 有些外行看起来很复杂的需求 (如银行业务流程), 如果一个程序员已经做过多次相关的银行项目, 其实不向外人看的那么难。
b) 技术的复杂程度 - 程序员是第几次用这个技术实现?
一个极端的例子: 几个程序员用他们从来没用过的技术 (例如 HTML5) 去实现一个他们以前没碰到过的需求 (例如银行业务), 他们的时间估计一定很飘忽...
业界的专家也有类似的分析, 例如这个项目/过程复杂度的二维图 (图来自 Danc “Managing game design risk: Part I” )
一个案例: 大牛在完成一项任务, 他原计划 3 天完成, 现在是第三天的下午, 他马上就可以做完. 但是在实现功能的过程中, 他越来越意识到自己原来的想法不是最好, 他应该采取另一个办法, 才能避免后面集成阶段的额外工作. 但是他如果现在就改弦更张, 那势必要影响自己原来估计的准确性. 这样他的老板, 同事会因此看不起他? 如果他按部就班, 最后整个团队还要花更多时间在后续集成上, 但是就不是他个人的问题了. 怎么办?
整个软件项目的时间估计也可以从两个方面来看 -
a) 自底向上 团队成员各自估计底层模块和单个功能 (和单元测试) 所需的时间, 再加上集成, 及基本测试的时间, 就是大概的开发时间。 这还没有考虑各个模块之间的相互依赖性.
b) 回溯 团队从整个项目最终交付之日往回倒推 -
如果在十一就要交付整个软件, 那么九月一号就要完成基本测试
如果九月一号要完成基本测试, 那么八月一号就要代码完成 (Code Complete)
如果八月一号要代码完成, 那么我们要有16 周的开发任务, 那意味着我们四月一号就要开始, 而且四月一号要有第一批设计规格说明书 (spec)
我倒! 今天已经四月七号了! 你还在看博客!
在敏捷开发的项目中, 团队一般不过分强调 “估计”的价值,因为它就是一个“猜”字。 “猜得准”不是团队的目标。 团队的目标是把软件写出来, 让用户满意。 如果猜错了,没关系,微调项目进度即可,不要为了“猜得准” 而踌躇不前; 或者为了让当初的猜测看起来靠谱而不如实报告进度。
在敏捷的开发流程中, 还有不少看似山寨的办法, 我接触到的有:
估计扑克牌 – 扑克牌上面是1, 2, 3, 5, 8, 13, … 等数字, 大家出牌来估计某功能花费的时间。 这副牌我给了我们项目的PM, 她拿去打拖拉机了。
划拳估计法 - 几人一声呐喊, 同时出拳, 几个手指代表几天, 我们项目组还没有正式演练过.
t-shirt 尺寸法 – 用 S, M, L, XL 代表估计的时间长度, 对于尺寸超大的任务, 要考虑把它们分解为比较细小可掌控的小任务.
这些方法都是强调快速得到粗粒度的估计, 然后进入实现阶段. 一个团队经过一次里程碑之后, 再回过头看看原来的估计和实际花费时间的差距。 经过一两次里程碑, 成员们就可以了解在我们项目中, 一个尺寸为 S 的任务大概要多少天。
关于时间估计, 这里有更多相关内容:
http://www.pmhut.com/agile-estimating-%E2%80%93-estimation-approaches
回到上一个博客提到的目标, 决心和估计的区别, 当一个程序员果冻听到大老板说 - 果冻, 这个项目十一要交付使用, 你估计能行么?
果冻首先想到的不是用哪一种时间估计方法, 而应该反问 - 老板, 您已经给了一个商业目标, 现在你是想听客观的估计呢? 还是我主观的决心?
老板一定会对果冻另眼相看的 ![]()
另一个目标/决心/估计的故事: 某项目本来进行得很顺利, 大领导非要全体人员脱产开一天的动员大会, 会议结束时, 领导热情地问大家: 大家对如期完成项目有信心么? 这时, 项目经理站起来说: 我们本来是可以按期完成的, 现在开了一天会, 我们已经延期了一天。 对这样的经理, 我要点【赞】。
Steve McConnel 曾经详细说明了软件估计的 10 种罪, 很值得一读:
http://www.ewh.ieee.org/r5/central_texas/austin_cs/presentations/2004.08.26.pdf
既然是一个面试问题, 下面是我的一些打分标准:
- 能用靠谱的模型推算出中国陆地边界的长度, 1 分。
- 直接用长度除以人步行速度, -1 分.
- 在面试中能反问面试官的各种假设, 3 分.
- 能在多轮迭代中收敛估算值, 2 分.
- 能提出人的培训问题, 2 分
- 能提出人的投入及变动问题, 2 分
- 在别人提出不同模型后, 不加分析而坚持己见的, –5 分
- 在讨论中不敢坚持自己分析的, –5 分
- 能提出目标 / 估计 / 决心 的区别的, 2 分。
- 能提出几种不同的估计方法的, 3 分.
6 分及格, 10分优秀。 ![]()