C++二叉树的遍历：深度优先（前序、中序、后序）和广度优先（层次）

准备

二叉树（Binary Tree）是一种特殊的树型结构，它的特点是每个结点至多有两棵子树（即二叉树中不存在度大于2的结点），且二叉树的子树有左右之分，其次序不能任意颠倒（有序树）。相关内容可自行学习。

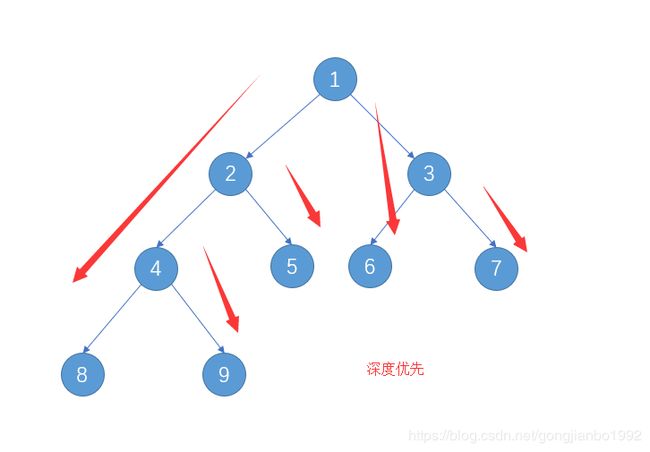
深度优先遍历：沿着每一个分支路径进行深入访问。前序、中序、后序都是深度优先遍历的特例。可以用递归实现，非递归一般借助Stack栈容器。

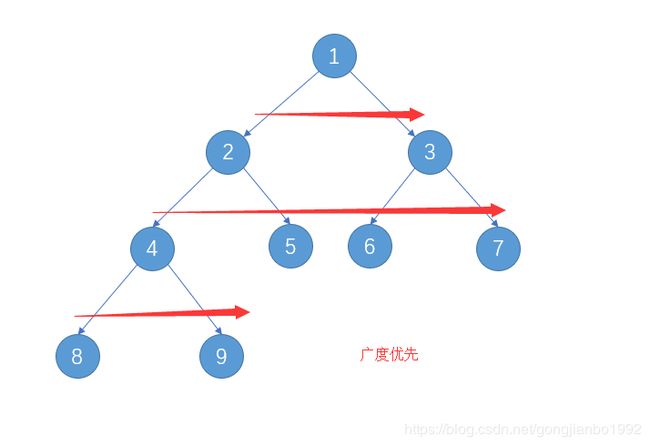
广度优先遍历：又叫层次遍历，对每一层依次访问。可以借助队Queue列容器来实现。

先定义和创建一颗二叉树

#include 
#include 
#include 
#include 

//定义二叉树结点
template
struct Node
{
	T value;
	Node *left;
	Node *right;

	Node(const T &val)
		:value(val), left(nullptr), right(nullptr)
	{}
	Node(const T &val, Node *&lnode, Node *&rnode)
		:value(val), left(lnode), right(rnode)
	{}
};

//创建二叉树
template
Node* createBinaryTree(const std::initializer_list &list)
{
	std::vector*> vec;
	for (auto &item : list)
	{
		Node *newNode = new Node(item);
		vec.push_back(newNode);
	}
	for (std::size_t i = 0; i < vec.size(); i++)
	{
		if (i * 2 + 1 < vec.size())
			vec[i]->left = vec[i * 2 + 1];
		if (i * 2 + 2 < vec.size())
			vec[i]->right = vec[i * 2 + 2];
	}
	return vec[0];
}

//删除二叉树
template
void deleteBinaryTree(Node *&rootNode)
{
	if (!rootNode)
		return;
	deleteBinaryTree(rootNode->left);
	deleteBinaryTree(rootNode->right);
	delete rootNode;
	rootNode = nullptr;
}

int main()
{
	Node *test = createBinaryTree({ 1, 2, 3, 4, 5, 6, 7 ,8,9 });//创建

	preorder(test);//前序--递归
	std::cout << endl;
	preorder2(test);//前序--非递归
	std::cout << endl;
	inorder(test);//中序--递归
	std::cout << endl;
	inorder2(test);//中序--非递归
	std::cout << endl;
	postorder(test);//后续--递归
	std::cout << endl;
	postorder2(test);//后续--非递归
	std::cout << endl;
	breadthFirst(test);//层次
	std::cout << endl;
	

	deleteBinaryTree(test);//释放

    system("pause");
    return 0;
}

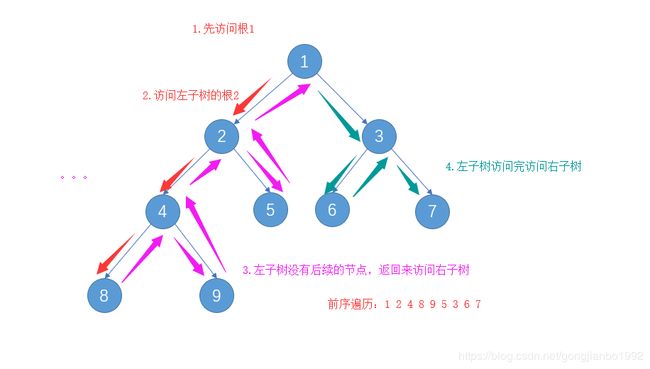
前序遍历 

前序遍历先访问根节点，再访问左右子树。

//前序遍历 --递归
template
void preorder(Node *&rootNode)
{
	if (!rootNode)
		return;
	//根->左->右
	std::cout << rootNode->value << " ";
	preorder(rootNode->left);
	preorder(rootNode->right);
}

//前序遍历 --栈
template
void preorder2(Node *&rootNode)
{
	std::stack*> nodeStack;
	Node *tempNode = rootNode;

	while (!nodeStack.empty() || tempNode)
	{
		if (tempNode) { 
			std::cout << tempNode->value<<" ";
			nodeStack.push(tempNode);
			tempNode = tempNode->left;//根->左
		}
		else { 
			tempNode = nodeStack.top();
			nodeStack.pop();
			tempNode = tempNode->right;//右
		}
	}
}

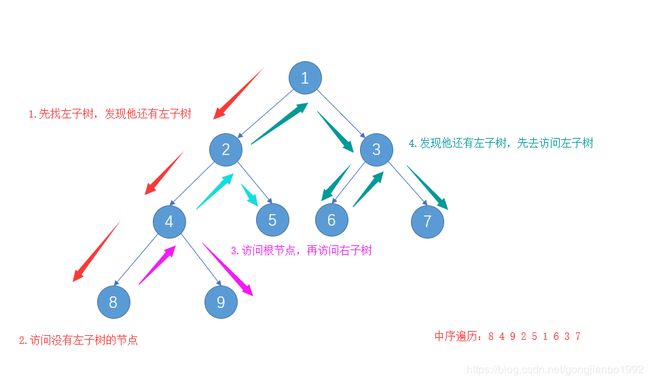
中序遍历 

中序遍历，访问根节点的次序在其左右子树之间。

//中序遍历 --递归
template
void inorder(Node *&rootNode)
{
	if (!rootNode)
		return;
	//左->根->右	
	inorder(rootNode->left);
	std::cout << rootNode->value << " ";
	inorder(rootNode->right);
}

//中序遍历 --栈
template
void inorder2(Node *&rootNode)
{
	std::stack*> nodeStack;
	Node *tempNode = rootNode;

	while (!nodeStack.empty() || tempNode)
	{
		if (tempNode) {
			nodeStack.push(tempNode);
			tempNode = tempNode->left;//左
		}
		else {
			tempNode = nodeStack.top();
			nodeStack.pop();
			std::cout << tempNode->value << " ";
			tempNode = tempNode->right;//根->右
		}
	}
}

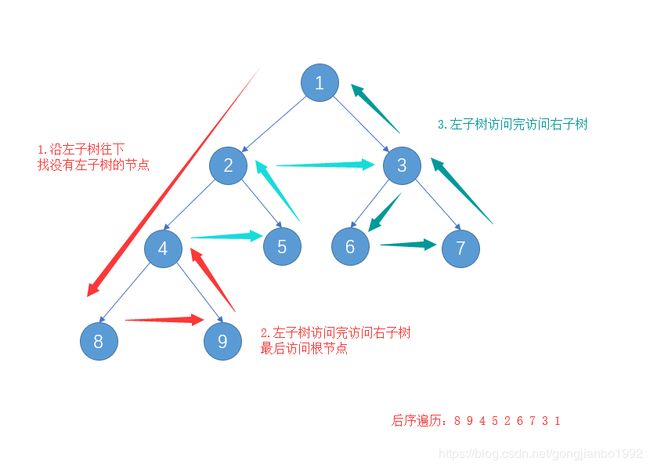
后序遍历

后序遍历先访问左右子树，最后才访问根节点 。

//后序遍历 --递归
template
void postorder(Node *&rootNode)
{
	if (!rootNode)
		return;
	//左->右->根	
	postorder(rootNode->left);
	postorder(rootNode->right);
	std::cout << rootNode->value << " ";
}

//后序遍历 --栈
template
void postorder2(Node *&rootNode)
{
	std::stack*> nodeStack;
	Node *curNode = rootNode; //当前节点
	Node *preNode = nullptr; //之前访问过的节点，用来存

	//把cur移动到左子树最下边
	while (curNode)
	{
		nodeStack.push(curNode);
		curNode = curNode->left;
	}
	while (!nodeStack.empty())
	{
		//走到这里，cur空，并已经遍历到左子树底端
		curNode = nodeStack.top();
		nodeStack.pop();
		//无右或右已访问才访问根节点
		if (!curNode->right || curNode->right == preNode){
			std::cout << curNode->value << " ";
			preNode = curNode;
		}
		//右子树未访问
		else{
			//根节点再次入栈
			nodeStack.push(curNode);
			//进入右子树
			curNode = curNode->right;
			//把cur移动到右子树的左子树最下边
			while (curNode)
			{
				nodeStack.push(curNode);
				curNode = curNode->left;
			}
		}
	}
}

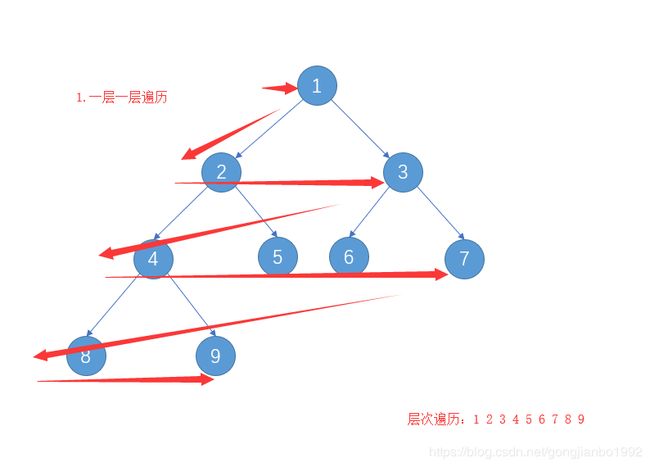
层次遍历 

层次遍历从上到下一层一层的遍历。

用队列的话，每访问一层，都把左右子树入栈，相当于把下一层入栈。出栈时，顺序也就是一层一层的了。 

//广度优先 --队列
template
void breadthFirst(Node *&rootNode)
{
	if (!rootNode)
		return;

	std::queue*> nodeQueue;
	Node *tempNode = nullptr;

	nodeQueue.push(rootNode);
	while (!nodeQueue.empty())
	{
		tempNode = nodeQueue.front();
		std::cout << tempNode->value << " ";
		nodeQueue.pop();
		if (tempNode->left)
			nodeQueue.push(tempNode->left);
		if (tempNode->right)
			nodeQueue.push(tempNode->right);
	}
}

参考

博客：https://blog.csdn.net/z_ryan/article/details/80854233

博客：https://blog.csdn.net/qq_40772692/article/details/79343914

博客：https://blog.csdn.net/hansionz/article/details/81947834