中国市场的三因子模型简单实践(1)_基于python(简单使用)
参考论文:《中国股票市场的三因子模型》——范龙振,余世典。
数据:2016-01——2019-03 国泰安
单个因素对股票回报率的影响
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df_retdata = pd.read_csv('trd_m.csv').dropna()
df_retdata['tt_value'] = np.log10(df_retdata['Msmvttl'])
df_retdata['lq_value'] = np.log10(df_retdata['Msmvosd'])
print(df_retdata.head())
#大概先看下总市值的对数与收益率有什么关系
trddate_list = set(df_retdata['Trdmnt'])
for date_i in trddate_list:
df_i = df_retdata[df_retdata['Trdmnt']==date_i]
plt.scatter(df_retdata.tt_value,df_retdata.Mretwd)
plt.show()
结果显示每个月份市值与个股票的月回报率之间的散点图很相似,而且没有十分明显的线性关系,倒是确实有论文中讲的市值效应、市值较大的收益率反而较低,是指较小的有着比较高的回报率,并且我发现市值再在106.5 到107.5 之间回报率最高。

进行简单的线性回归、虽然觉得这样子的关系肯定得不到什么理想的函数关系,金融系统是很复杂的…
#对每个月的所有股票进行一次回归,求各个月β_t,α_t
from sklearn.linear_model import LinearRegression
trddate_list = set(df_retdata['Trdmnt'])
b = list()#定义β_t系列
a = list()#定义α_t系列
R_2 = list()#定义拟合优度R^2
for date_i in trddate_list:
df_i = df_retdata[df_retdata['Trdmnt']==date_i]
x = df_i['tt_value'].values.reshape(-1,1)
y = df_i['Mretwd'].values.reshape(-1,1)
reg = LinearRegression().fit(x[:-6],y[6:])
b.append(reg.coef_[0][0])
a.append(reg.intercept_[0])
R_2.append(reg.score(x,y))
print("一元回归方程为: Y = %.5fX + (%.5f)" % (reg.coef_[0][0], reg.intercept_[0]))
print("R平方为: %s" % reg.score(x,y))
下面计算R2 可以略过,因为在因子模型中不用这个变量来衡量,这里只是简单的看下所拟合的函数是否具有统计意义
拟合优度 R2 计算:
设总体平方和为:
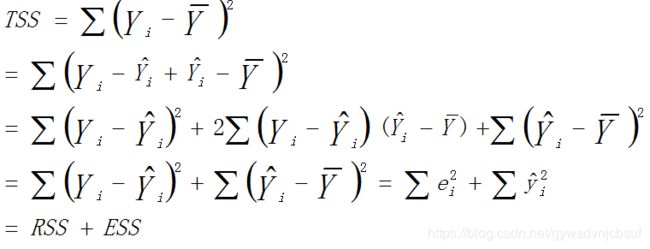
回归平方和:
![]()
残差平方和:
![]()
即 TSS=ESS+RSS
样本中,TSS不变, 如果实际观测点离样本回归线越近,则ESS在TSS中占的比重越大.
拟合优度:
![]()
R2 为(样本)可决系数/判定系数(coefficient of determination),取值范围:[0,1]。R2越接近1,说明实际观测点离样本线越近,拟合优度越高。一般地要求R2≥0.7。
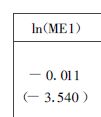
论文的Fama-Mecbath判定法
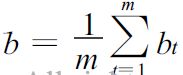
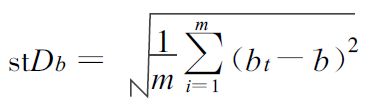
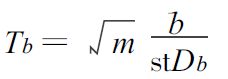
根据Fama-Mecbath的看法,在一定假设下,T统计量可以用来检验因素对回报率是否有显著的影响。
先放几张拟合效果图
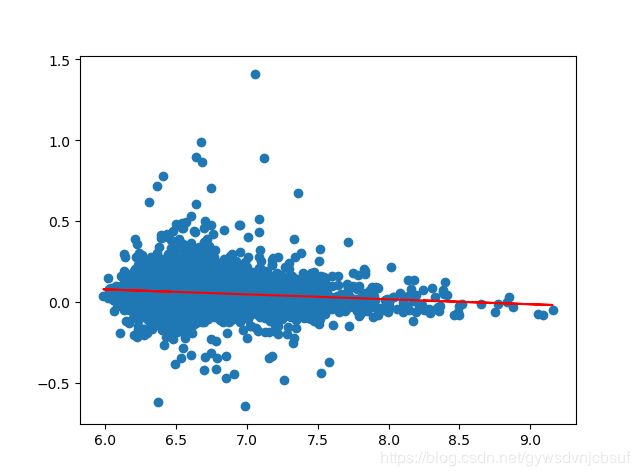
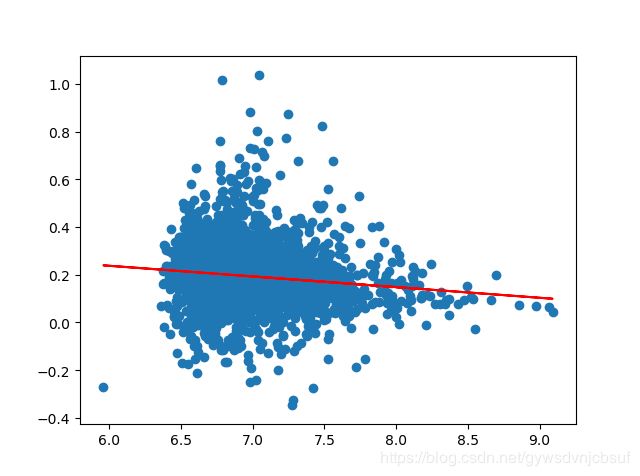
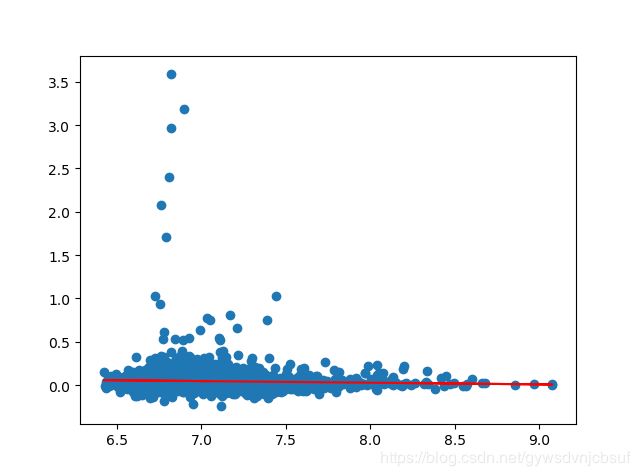
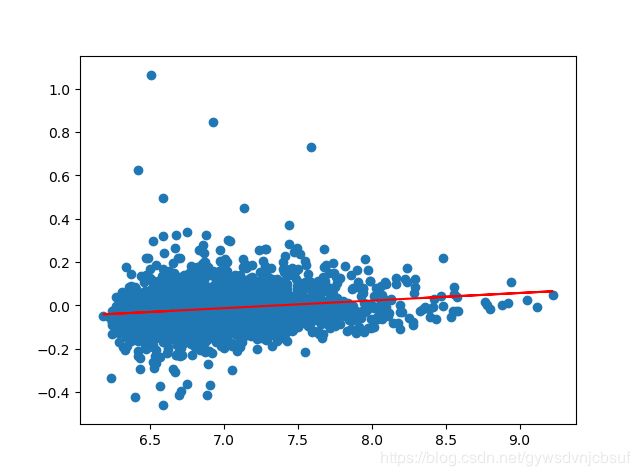
基本上是每个月的总市值和回报率呈现正相关的关系,这与论文相反,不知道是不是最近几年的市场行情与1996—2000不太一样了。。。回头再试试。。。。
下面是总市值的Fama-Mecbath检验结果:
| β平均值 | 0.01995967386043265 |
|---|---|
| T检验量 | 3.0457386436275162 |
2、接下来同样的套路,继续研究其他市场因子——市盈率
暂时还没有下载相应的数据,改天更新…